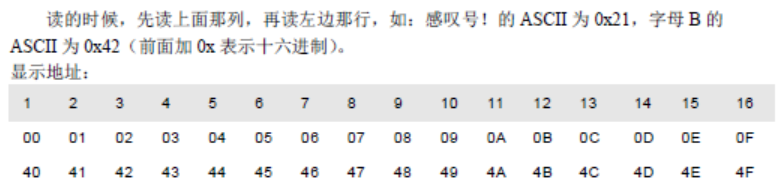
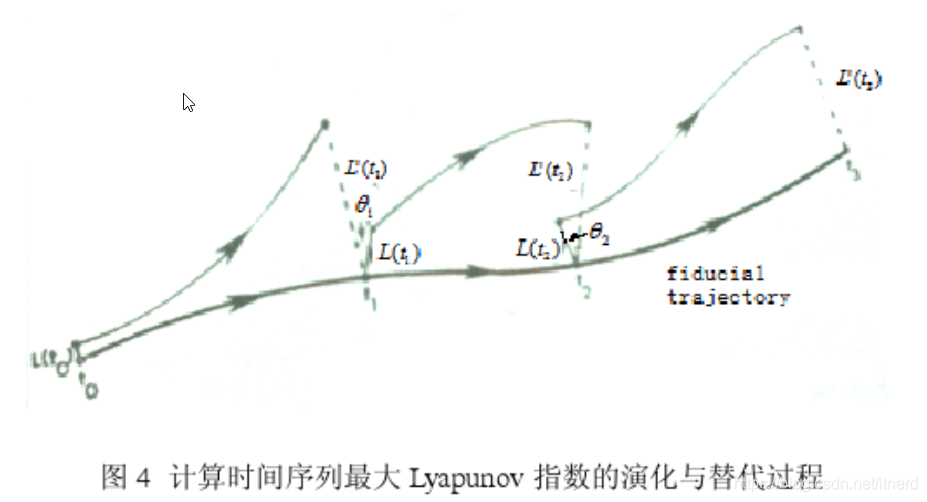
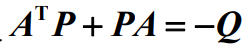单片机控制LCD1602显示英文句子

article/2025/9/22 14:42:50

LCD1602简介：

1602字符型液晶也叫1602液晶，它是一种专门用来显示字母、数字、符号等的点阵型液晶模块。字符型液晶，能够同时显示16x02即32个字符。
它由若干个5X7或者5X11等点阵字符位组成，每个点阵字符位都可以显示一个字符，每位之间有一个点距的间隔，每行之间也有间隔，起到了字符间距和行间距的作用，正因为如此所以它不能很好地显示图形（用自定义CGRAM，显示效果也不好）。

-------------------------- 在这里插入图片描述

仿真图像：

在这里插入图片描述

C语言程序：

/*-----------------------------------------------
内容：通过标准程序静态显示字符
引脚定义如下：1-VSS 2-VDD 3-V0 4-RS 5-R/W 6-E 7-14 DB0-DB7 15-BLA 16-BLK
------------------------------------------------*/
#include<reg52.h> //包含头文件，一般情况不需要改动，头文件包含特殊功能寄存器的定义
#include<intrins.h>sbit RS = P2^4;   //定义端口 
sbit RW = P2^5;
sbit EN = P2^6;#define RS_CLR RS=0 
#define RS_SET RS=1#define RW_CLR RW=0 
#define RW_SET RW=1 #define EN_CLR EN=0
#define EN_SET EN=1#define DataPort P0
/*------------------------------------------------
uS延时函数，含有输入参数 unsigned char t，无返回值
unsigned char 是定义无符号字符变量，其值的范围是
0~255 这里使用晶振12M，精确延时请使用汇编,大致延时
长度如下 T=tx2+5 uS 
------------------------------------------------*/
void DelayUs2x(unsigned char t)
{   while(--t);
}
/*------------------------------------------------
mS延时函数，含有输入参数 unsigned char t，无返回值
unsigned char 是定义无符号字符变量，其值的范围是
0~255 这里使用晶振12M，精确延时请使用汇编
------------------------------------------------*/
void DelayMs(unsigned char t)
{  while(t--){//大致延时1mSDelayUs2x(245);DelayUs2x(245);}
}
/*------------------------------------------------
判忙函数
------------------------------------------------*/
bit LCD_Check_Busy(void) 
{ DataPort= 0xFF; RS_CLR; RW_SET; EN_CLR; _nop_(); EN_SET;return (bit)(DataPort & 0x80);
}
/*------------------------------------------------
写入命令函数
------------------------------------------------*/
void LCD_Write_Com(unsigned char com) 
{  // while(LCD_Check_Busy()); //忙则等待DelayMs(5);RS_CLR; RW_CLR; EN_SET; DataPort= com; _nop_(); EN_CLR;
}
/*------------------------------------------------
写入数据函数
------------------------------------------------*/
void LCD_Write_Data(unsigned char Data) 
{ //while(LCD_Check_Busy()); //忙则等待DelayMs(5);RS_SET; RW_CLR; EN_SET; DataPort= Data; _nop_();EN_CLR;
}/*------------------------------------------------
清屏函数
------------------------------------------------*/
void LCD_Clear(void) 
{ LCD_Write_Com(0x01); DelayMs(5);
}
/*------------------------------------------------
写入字符串函数
------------------------------------------------*/
void LCD_Write_String(unsigned char x,unsigned char y,unsigned char *s) 
{     if (y == 0) {     LCD_Write_Com(0x80 + x);     //表示第一行}else {      LCD_Write_Com(0xC0 + x);      //表示第二行}        while (*s) {     LCD_Write_Data( *s);     s ++;     }
}
/*------------------------------------------------
写入字符函数
------------------------------------------------*/
void LCD_Write_Char(unsigned char x,unsigned char y,unsigned char Data) 
{     if (y == 0) {     LCD_Write_Com(0x80 + x);     }    else {     LCD_Write_Com(0xC0 + x);     }        LCD_Write_Data( Data);  
}
/*------------------------------------------------
初始化函数
------------------------------------------------*/
void LCD_Init(void) 
{LCD_Write_Com(0x38);    /*显示模式设置*/ DelayMs(5); LCD_Write_Com(0x38); DelayMs(5); LCD_Write_Com(0x38); DelayMs(5); LCD_Write_Com(0x38);  LCD_Write_Com(0x08);    /*显示关闭*/ LCD_Write_Com(0x01);    /*显示清屏*/ LCD_Write_Com(0x06);    /*显示光标移动设置*/ DelayMs(5); LCD_Write_Com(0x0C);    /*显示开及光标设置*/
}/*------------------------------------------------
主函数[上面已经把显示功能封装好了，今后再写其他显示就直接调用]
------------------------------------------------*/ 
void main(void) 
{ LCD_Init(); LCD_Clear();//清屏while (1) {  LCD_Write_Char(7,0,'o');//单引号在C语言中表示取字符的ASCII码，这一行代码也可以写为：  LCD_Write_Char(7,0,0x6F);LCD_Write_Char(8,0,'k');LCD_Write_String(1,1,"I LOVE YOU!");//双引号在C语言中表示取字符串的ASCII码while(1);}
}