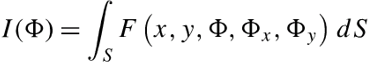AQS是AbstractQueuedSynchronizer的简称。AQS提供了一种实现阻塞锁和一系列依赖FIFO等待队列的同步器的框架,如下图所示。AQS为一系列同步器依赖于一个单独的原子变量(state)的同步器提供了一个非常有用的基础。子类们必须定义改变state变量的protected方法,这些方法定义了state是如何被获取或释放的。鉴于此,本类中的其他方法执行所有的排队和阻塞机制。子类也可以维护其他的state变量,但是为了保证同步,必须原子地操作这些变量。
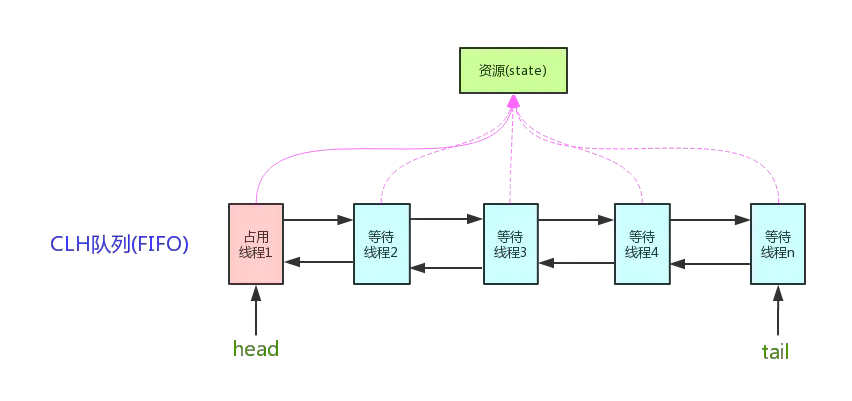
使用一个volatile的int类型的state表示同步状态,通过内置的FIFO队列CLH完成资源获取的排队工作,将资源封装为Node,通过cas改变state值
AQS同时提供了互斥模式(exclusive)和共享模式(shared)两种不同的同步逻辑。一般情况下,子类只需要根据需求实现其中一种模式,当然也有同时实现两种模式的同步类,如ReadWriteLock。
state状态
AbstractQueuedSynchronizer维护了一个volatile int类型的变量,用户表示当前同步状态。volatile虽然不能保证操作的原子性,但是保证了当前变量state的可见性。
/*** The synchronization state.*/private volatile int state;/*** Returns the current value of synchronization state.* This operation has memory semantics of a {@code volatile} read.* @return current state value*/protected final int getState() {return state;}/*** Sets the value of synchronization state.* This operation has memory semantics of a {@code volatile} write.* @param newState the new state value*/protected final void setState(int newState) {state = newState;}/*** Atomically sets synchronization state to the given updated* value if the current state value equals the expected value.* This operation has memory semantics of a {@code volatile} read* and write.** @param expect the expected value* @param update the new value* @return {@code true} if successful. False return indicates that the actual* value was not equal to the expected value.*/protected final boolean compareAndSetState(int expect, int update) {// See below for intrinsics setup to support thisreturn unsafe.compareAndSwapInt(this, stateOffset, expect, update);}
自定义资源共享方式
AQS定义两种资源共享方式:Exclusive(独占,只有一个线程能执行,如ReentrantLock)和Share(共享,多个线程可同时执行,如Semaphore/CountDownLatch)
不同的自定义同步器争用共享资源的方式也不同。自定义同步器在实现时只需要实现共享资源state的获取与释放方式即可,至于具体线程等待队列的维护(如获取资源失败入队/唤醒出队等),AQS已经在顶层实现好了。自定义同步器实现时主要实现以下几种方法:
isHeldExclusively():该线程是否正在独占资源。只有用到condition才需要去实现它。
tryAcquire(int):独占方式。尝试获取资源,成功则返回true,失败则返回false。
tryRelease(int):独占方式。尝试释放资源,成功则返回true,失败则返回false。
tryAcquireShared(int):共享方式。尝试获取资源。负数表示失败;0表示成功,但没有剩余可用资源;正数表示成功,且有剩余资源。
tryReleaseShared(int):共享方式。尝试释放资源,如果释放后允许唤醒后续等待结点返回true,否则返回false。
源码实现
1.Lock
ReentrantLock -> Sync -> NonfairSync(非公平) -> acquire -> tryAcquire/addWaiter/acquireQueued/selfInterrupt
static final class NonfairSync extends Sync {private static final long serialVersionUID = 7316153563782823691L;/*** Performs lock. Try immediate barge, backing up to normal* acquire on failure.*/final void lock() {if (compareAndSetState(0, 1))setExclusiveOwnerThread(Thread.currentThread());elseacquire(1);}protected final boolean tryAcquire(int acquires) {return nonfairTryAcquire(acquires);}}
public final void acquire(int arg) {if (!tryAcquire(arg) &&acquireQueued(addWaiter(Node.EXCLUSIVE), arg))selfInterrupt();}
通过注释我们知道,acquire方法是一种互斥模式,且忽略中断。该方法至少执行一次tryAcquire(int)方法,如果tryAcquire(int)方法返回true,则acquire直接返回,否则当前线程需要进入队列进行排队。函数流程如下:
- tryAcquire()尝试直接去获取资源,如果成功则直接返回;
- addWaiter()将该线程加入等待队列的尾部,并标记为独占模式;
- acquireQueued()使线程在等待队列中获取资源,一直获取到资源后才返回。如果在整个等待过程中被中断过,则返回true,否则返回false。
- 如果线程在等待过程中被中断过,它是不响应的。只是获取资源后才再进行自我中断selfInterrupt(),将中断补上。
tryAcquire
protected boolean tryAcquire(int arg) {throw new UnsupportedOperationException();}
子类继承,没有实现的话直接抛出异常

final boolean nonfairTryAcquire(int acquires) {final Thread current = Thread.currentThread();int c = getState();if (c == 0) {if (compareAndSetState(0, acquires)) {setExclusiveOwnerThread(current);return true;}}else if (current == getExclusiveOwnerThread()) {int nextc = c + acquires;if (nextc < 0) // overflowthrow new Error("Maximum lock count exceeded");setState(nextc);return true;}return false;}
1.判断状态位是否为0,0是可以占用,如果是0的话占用,不是0的话返回false
2.判断当前线程是否为得到位置的线程,比如如果前一个线程走了,然后又回来有点事情的话,那么返回false
addWaiter
添加到队列的过程
private Node addWaiter(Node mode) {Node node = new Node(Thread.currentThread(), mode);// Try the fast path of enq; backup to full enq on failureNode pred = tail;if (pred != null) {node.prev = pred;if (compareAndSetTail(pred, node)) {pred.next = node;return node;}}enq(node);return node;}
第一次队列无Node的时候返回直接进入enq()方法,如果有Node话会进入if
if中有一个cas操作,比较和交换了头指针和当前Node。
使得当前进入的第三个Node和第二个Node接在了一起

enq
private Node enq(final Node node) {for (;;) {Node t = tail;if (t == null) { // Must initializeif (compareAndSetHead(new Node()))tail = head;} else {node.prev = t;if (compareAndSetTail(t, node)) {t.next = node;return t;}}}}
这里的一开始的头指针设置为空Node作为占位符。是傀儡节点,哨兵节点。
第二次进入的时候第二个节点的头节点指的是空节点,然后cas使得尾结点指向第二个节点。
哨兵节点的下一个节点指向第二个节点。于是形成了一个双向链表。

acquireQueued
final boolean acquireQueued(final Node node, int arg) {boolean failed = true;try {boolean interrupted = false;for (;;) {final Node p = node.predecessor();if (p == head && tryAcquire(arg)) {setHead(node);p.next = null; // help GCfailed = false;return interrupted;}if (shouldParkAfterFailedAcquire(p, node) &&parkAndCheckInterrupt())interrupted = true;}} finally {if (failed)cancelAcquire(node);}}
acquireQueued()用于队列中的线程自旋地以独占且不可中断的方式获取同步状态(acquire),直到拿到锁之后再返回。该方法的实现分成两部分:如果当前节点已经成为头结点,尝试获取锁(tryAcquire)成功,然后返回;否则检查当前节点是否应该被park,然后将该线程park并且检查当前线程是否被可以被中断。
shouldParkAfterFailedAcquire
shouldParkAfterFailedAcquire方法通过对当前节点的前一个节点的状态进行判断,对当前节点做出不同的操作,至于每个Node的状态表示。也是为了解决哨兵节点的waitState从0改为-1。于是可以操作后面的节点。判断后面的节点是否进行park
private static boolean shouldParkAfterFailedAcquire(Node pred, Node node) {// 获取当前节点状态int ws = pred.waitStatus;// 如果是SIGNAL的话,线程被释放,返回trueif (ws == Node.SIGNAL)return true;// ws大于0表示ws = 1if (ws > 0) {do {node.prev = pred = pred.prev;} while (pred.waitStatus > 0);pred.next = node;} else {compareAndSetWaitStatus(pred, ws, Node.SIGNAL);}return false;}
parkAndCheckInterrupt()
该方法让线程去休息,真正进入等待状态。park()会让当前线程进入waiting状态。在此状态下,有两种途径可以唤醒该线程:1)被unpark();2)被interrupt()。需要注意的是,Thread.interrupted()会清除当前线程的中断标记位。
private final boolean parkAndCheckInterrupt() {LockSupport.park(this);return Thread.interrupted();}
这个方法才是真正让线程进入等待状态进入waiting状态。
1.自己unpark 2.被中断
总结
- 调用自定义同步器的tryAcquire()尝试直接去获取资源,如果成功则直接返回;
- 没成功,则addWaiter()将该线程加入等待队列的尾部,并标记为独占模式;
- acquireQueued()使线程在等待队列中休息,有机会时(轮到自己,会被unpark())会去尝试获取资源。获取到资源后才返回。如果在整个等待过程中被中断过,则返回true,否则返回false。
- 如果线程在等待过程中被中断过,它是不响应的。只是获取资源后才再进行自我中断selfInterrupt(),将中断补上。
2.unlock
unlock -> release -> tryrelease ->
public void unlock() {sync.release(1);}
release
public final boolean release(int arg) {if (tryRelease(arg)) {Node h = head;if (h != null && h.waitStatus != 0)unparkSuccessor(h);return true;}return false;}
tryRelease
protected final boolean tryRelease(int releases) {int c = getState() - releases;if (Thread.currentThread() != getExclusiveOwnerThread())throw new IllegalMonitorStateException();boolean free = false;if (c == 0) {free = true;setExclusiveOwnerThread(null);}setState(c);return free;}
与acquire()方法中的tryAcquire()类似,tryRelease()方法也是需要独占模式的自定义同步器去实现的。正常来说,tryRelease()都会成功的,因为这是独占模式,该线程来释放资源,那么它肯定已经拿到独占资源了,直接减掉相应量的资源即可(state-=arg),也不需要考虑线程安全的问题。但要注意它的返回值,上面已经提到了,release()是根据tryRelease()的返回值来判断该线程是否已经完成释放掉资源了!所以自义定同步器在实现时,如果已经彻底释放资源(state=0),要返回true,否则返回false。
unparkSuccessor(Node)方法用于唤醒等待队列中下一个线程。这里要注意的是,下一个线程并不一定是当前节点的next节点,而是下一个可以用来唤醒的线程,如果这个节点存在,调用unpark()方法唤醒。
总之,release()是独占模式下线程释放共享资源的顶层入口。它会释放指定量的资源,如果彻底释放了(即state=0),它会唤醒等待队列里的其他线程来获取资源。




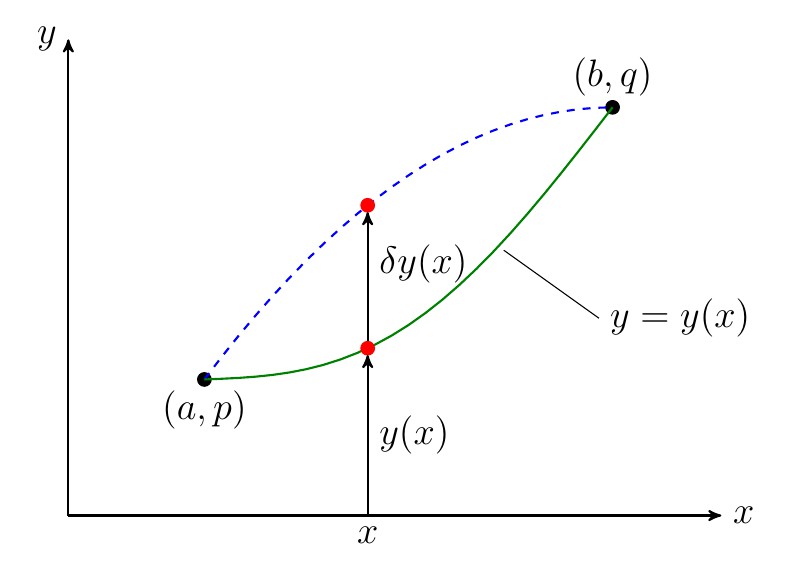
![[变分法介绍]优美的旋轮线:最速下降线问题,通过费马光学原理的初等证明](https://img-blog.csdnimg.cn/20200621210611999.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MzcwMDczMg==,size_16,color_FFFFFF,t_70#pic_center)