变分法

弦平衡方程的导出，建立起横向位移u，张力T，外力f之间的关系：

方一、根据受力平衡导出


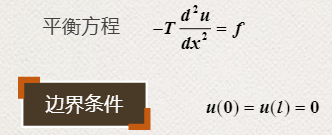
推导时用的技巧或假设：
1.泰勒展开近似      同理
2.
3.小变形假设，张力均匀，即
4.方程推导中忽略二阶小量，即只要某一项带就忽略掉他。

方二、根据总势能最小导出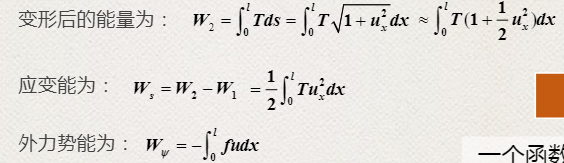


u是x的函数，J是u的函数，求J的min，即求极值，求泛函的极值即变分问题

v为试探函数，此时将问题从对泛函求极值转化为对函数求极值，即J(u(x))求极值转化为J(λ)，这种方法为变分法

推导时用到的技巧：
1、
2、泰勒展开近似
3、分部积分法
4、小变形假设，张力均匀，即

注：表示二元复数对的集合，也表示二阶导连续，这里指在0到L上函数二阶导连续

两种方法推导出的平衡方程一个是积分形式，一个是微分形式。
变分方程要求u一阶可导，积分存在，欧拉方程（受力平衡方程）要求u二阶可导。

将变分方程进行分部积分展开，可以看出其与欧拉方程的联系

即求解微分方程Lu=f，L为微分算子，通过一个积分方程来求u。

变分问题的近似解法

因为用线性算子方便表达

对变分问题进行近似——Ritz法

感觉和摄动理论差不多

J对Cj求偏导，然后用线性算子的性质化简，得到一个方程

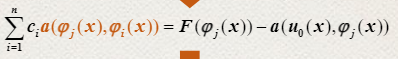
j=1~n的方程组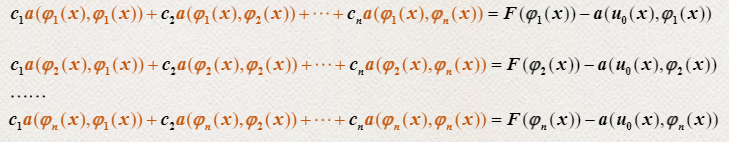

写作矩阵形式

对变分方程进行近似——Galerkin法

同样的方法

总之这种设解的方法与摄动理论差不多。

后面的一些其他内容

自治系统

数学模型用来描述某一系统，动态系统用微分方程描述，自治系统是动态系统的一种。

一元自治系统的方程

二元自治系统的方程

例子：种群竞争模型、捕食者-食饵模型

扩散方程

广义的扩散是质量、动量、能量的扩散，狭义的扩散：质量的扩散。所以广义上扩散方程包括：波动方程、NS方程、热传导方程、扩散方程（质量扩散，由于浓度差造成）。

瞬时点源扩散问题：比如装满石油的轮船泄露，求海水某时刻某位置的石油浓度。