一文让你彻底搞懂AQS(通俗易懂的AQS)
一、什么是AQS
- AQS是一个用来构建锁和同步器的框架,使用AQS能简单且高效地构造出应用广泛的大量的同步器,比如我们提到的ReentrantLock,Semaphore,其他的诸如ReentrantReadWriteLock,SynchronousQueue,FutureTask等等皆是基于AQS的。当然,我们自己也能利用AQS非常轻松容易地构造出符合我们自己需求的同步器。
二、前置知识
- 学习AQS需要大家对同步锁有一定的概念。同时大家要知道LockSupport的使用,可以参考我这篇文章。(LockSupport从入门到深入理解)
三、AQS 的核心思想
- AQS核心思想是,如果被请求的共享资源空闲,则将当前请求资源的线程设置为有效的工作线程,并且将共享资源设置为锁定状态。如果被请求的共享资源被占用,那么就需要一套线程阻塞等待以及被唤醒时锁分配的机制,这个机制AQS是用CLH队列锁实现的,即将暂时获取不到锁的线程加入到队列中。 CLH(Craig,Landin,and Hagersten)队列是一个虚拟的双向队列(虚拟的双向队列即不存在队列实例,仅存在结点之间的关联关系)。AQS是将每条请求共享资源的线程封装成一个CLH锁队列的一个结点(Node)来实现锁的分配。 AQS使用一个int成员变量来表示同步状态,通过内置的FIFO队列来完成获取资源线程的排队工作。AQS使用CAS对该同步状态进行原子操作实现对其值的修改。 (图一为节点关系图)
private volatile int state;//共享变量,使用volatile修饰保证线程可见性

四、AQS 案例分析
上面讲述的原理还是太抽象了,那我我们上示例,结合案例来分析AQS 同步器的原理。以ReentrantLock使用方式为例。
代码如下:
public class AQSDemo {private static int num;public static void main(String[] args) {ReentrantLock lock = new ReentrantLock();new Thread(new Runnable() {@Overridepublic void run() {lock.lock();try {Thread.sleep(1000);num += 1000;System.out.println("A 线程执行了1秒,num = "+ num);} catch (InterruptedException e) {e.printStackTrace();}finally {lock.unlock();}}},"A").start();new Thread(new Runnable() {@Overridepublic void run() {lock.lock();try {Thread.sleep(500);num += 500;System.out.println("B 线程执行了0.5秒,num = "+ num);} catch (InterruptedException e) {e.printStackTrace();}finally {lock.unlock();}}},"B").start();new Thread(new Runnable() {@Overridepublic void run() {lock.lock();try {Thread.sleep(100);num += 100;System.out.println("C 线程执行了0.1秒,num = "+ num);} catch (InterruptedException e) {e.printStackTrace();}finally {lock.unlock();}}},"C").start();}
}执行的某一种结果! 这个代码超级简单,但是执行结果却是可能不一样,大家可以自行实验。
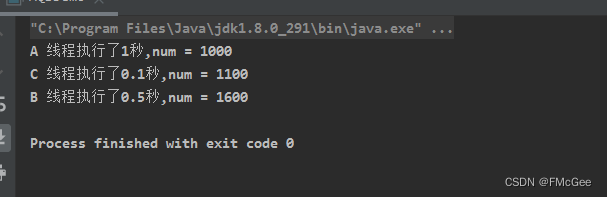
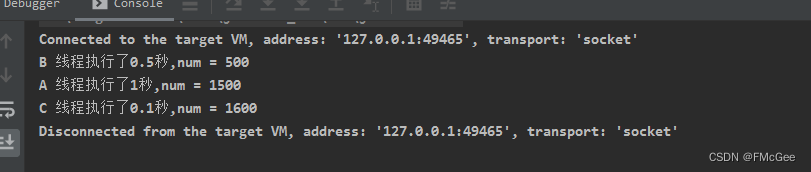
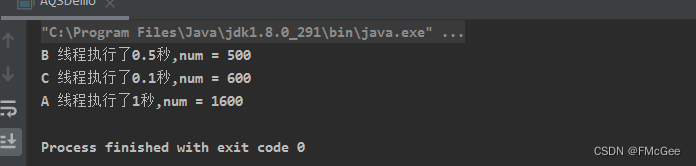
对比一下三种结果,大家会发现,无论什么样的结果,num最终的值总是1600,这说明我们加锁是成功的。
五、AQS 源码分析
- 使用方法很简单,线程操纵资源类就行。主要方法有两个lock() 和unlock().我们深入代码去理解。我在源码的基础上加注释,希望大家也跟着调试源码。其实非常简单。
5.1 AQS 的数据结构
AQS 主要有三大属性分别是 head ,tail, state,其中state 表示同步状态,head为等待队列的头结点,tail 指向队列的尾节点。
/*** Head of the wait queue, lazily initialized. Except for* initialization, it is modified only via method setHead. Note:* If head exists, its waitStatus is guaranteed not to be* CANCELLED.*/private transient volatile Node head;/*** Tail of the wait queue, lazily initialized. Modified only via* method enq to add new wait node.*/private transient volatile Node tail;/*** The synchronization state.*/private volatile int state;
还需要再去了解 Node的数据结构,
在这里插入代码片
class Node{//节点等待状态volatile int waitStatus;// 双向链表当前节点前节点volatile Node prev;// 下一个节点volatile Node next;// 当前节点存放的线程volatile Thread thread;// condition条件等待的下一个节点Node nextWaiter;
}
waitStatus 只有特定的几个常量,相应的值解释如下:

本次源码讲解,我们一ReentranLock的非公平锁为例。我们主要关注的方法是lock(),和unlock()。
5.2 lock源码分析
首先我们看一下lock()方法源代码,直接进入非公平锁的lock方法:
final void lock() {//1、判断当前state 状态, 没有锁则当前线程抢占锁if (compareAndSetState(0, 1))// 独占锁setExclusiveOwnerThread(Thread.currentThread());else// 2、锁被人占了,尝试获取锁,关键方法了acquire(1);}
进入 AQS的acquire() 方法:
public final void acquire(int arg) {if (!tryAcquire(arg) &&acquireQueued(addWaiter(Node.EXCLUSIVE), arg))selfInterrupt();}
总-分-总
- lock方法主要由tryAquire()尝试获取锁,addWaiter(Node.EXCLUSIVE) 加入等待队列,acquireQueued(node,arg)等待队列尝试获取锁。示意图如下:

5.2.1 tryAquire 方法源码
- 既然是非公平锁,那么我们一进来就想着去抢锁,不管三七二一,直接试试能不能抢到,抢不到再进队列。
final boolean nonfairTryAcquire(int acquires) {//1、获取当前线程final Thread current = Thread.currentThread();// 2、获取当前锁的状态,0 表示没有被线程占有,>0 表示锁被别的线程占有int c = getState();// 3、如果锁没有被线程占有if (c == 0) {// 3.1、 使用CAS去获取锁, 为什么用case呢,防止在获取c之后 c的状态被修改了,保证原子性if (compareAndSetState(0, acquires)) {// 3.2、设置独占锁setExclusiveOwnerThread(current);// 3.3、当前线程获取到锁后,直接发挥truereturn true;}}// 4、判断当前占有锁的线程是不是自己else if (current == getExclusiveOwnerThread()) {// 4.1 可重入锁,加+1int nextc = c + acquires;if (nextc < 0) // overflowthrow new Error("Maximum lock count exceeded");// 4.2 设置锁的状态setState(nextc);return true;}return false;}
5.2.2 addWaiter() 方法的解析
- private Node addWaiter(Node mode),当前线程没有货得锁的情况下,进入CLH队列。
private Node addWaiter(Node mode) {// 1、初始化当前线程节点,虚拟节点Node node = new Node(Thread.currentThread(), mode);// Try the fast path of enq; backup to full enq on failure// 2、获取尾节点,初始进入节点是nullNode pred = tail;// 3、如果尾节点不为null,怎将当前线程节点放到队列尾部,并返回当前节点if (pred != null) {node.prev = pred;if (compareAndSetTail(pred, node)) {pred.next = node;return node;}}// 如果尾节点为null(其实是链表没有初始化),怎进入enq方法enq(node);return node;}// 这个方法可以认为是初始化链表private Node enq(final Node node) {// 1、入队 : 为什么要用循环呢? for (;;) {// 获取尾节点Node t = tail;// 2、尾节点为nullif (t == null) { // Must initialize// 2.1 初始话头结点和尾节点if (compareAndSetHead(new Node()))tail = head;} // 3、将当前节点加入链表尾部else {node.prev = t;if (compareAndSetTail(t, node)) {t.next = node;return t;}}}}
有人想明白为什么enq要用for(;;)吗? 咋一看最多只要循环2次啊! 答疑来了,这是对于单线程来说确实是这样的,但是对于多线程来说,有可能在第2部完成之后就被别的线程先执行入链表了,这时候第3步cas之后发现不成功了,怎么办?只能再一次循环去尝试加入链表,直到成功为止。
5.2.3 acquireQueued()方法详解
- addWaiter 方法我们已经将没有获取锁的线程放在了等待链表中,但是这些线程并没有处于等待状态。acquireQueued的作用就是将线程设置为等待状态。
final boolean acquireQueued(final Node node, int arg) {// 失败标识boolean failed = true;try {// 中断标识boolean interrupted = false;for (;;) {// 获取当前节点的前一个节点final Node p = node.predecessor();// 1、如果前节点是头结点,那么去尝试获取锁if (p == head && tryAcquire(arg)) {// 重置头结点setHead(node);p.next = null; // help GC// 获得锁failed = false;// 返回false,节点获得锁,,,然后现在只有自己一个线程了这个时候就会自己唤醒自己// 使用的是acquire中的selfInterrupt(); return interrupted;}// 2、如果线程没有获得锁,且节点waitStatus=0,shouldParkAfterFailedAcquire并将节点的waitStatus赋值为-1//parkAndCheckInterrupt将线程park,进入等待模式,if (shouldParkAfterFailedAcquire(p, node) &&parkAndCheckInterrupt())interrupted = true;}} finally {if (failed)cancelAcquire(node);}}private static boolean shouldParkAfterFailedAcquire(Node pred, Node node) {int ws = pred.waitStatus;if (ws == Node.SIGNAL)/** This node has already set status asking a release* to signal it, so it can safely park.*/return true;if (ws > 0) {/** Predecessor was cancelled. Skip over predecessors and* indicate retry.*/do {node.prev = pred = pred.prev;} while (pred.waitStatus > 0);pred.next = node;} else {/** waitStatus must be 0 or PROPAGATE. Indicate that we* need a signal, but don't park yet. Caller will need to* retry to make sure it cannot acquire before parking.*/compareAndSetWaitStatus(pred, ws, Node.SIGNAL);}return false;}
- 好了,这个源码的解释就结束了,大家是不是还是云里雾里,不得不承认,这个代码太优雅了。不愧大神!
我用白话给大家串起来讲一下吧! 我们以reentrantLock的非公平锁结合我们案例4来讲解。
当线程A 到lock()方法时,通过compareAndSetState(0,1)获得锁,并且获得独占锁。当B,C线程去争抢锁时,运行到acquire(1),C线程运行tryAcquire(1),接着运行nonfairTryAcquire(1)方法,未获取锁,最后返回false,运行addWaiter(),运行enq(node),初始化head节点,同时C进入队列;再进入acquireQueued(node,1)方法,初始化waitStatus= -1,自旋并park()进入等待。
接着B线程开始去抢锁,B线程运行tryAcquire(1),运行nonfairTryAcquire(1)方法,未获得锁最后返回false,运行addWaiter(),直接添加到队尾,同时B进入队列;在进入acquireQueued(node,1)方法,初始化waitStatus= -1,自旋并park()进入等待。

5.3 unlock源码分析
unlock释放锁。主要利用的是LockSupport
public final boolean release(int arg) {// 如果成功释放独占锁,if (tryRelease(arg)) {Node h = head;// 如果头结点不为null,且后续有入队结点if (h != null && h.waitStatus != 0)//释放当前线程,并激活等待队里的第一个有效节点unparkSuccessor(h);return true;}return false;}// 如果释放锁着返回true,否者返回false// 并且将sate 设置为0protected final boolean tryRelease(int releases) {int c = getState() - releases;if (Thread.currentThread() != getExclusiveOwnerThread())throw new IllegalMonitorStateException();boolean free = false;if (c == 0) {free = true;setExclusiveOwnerThread(null);}setState(c);return free;}private void unparkSuccessor(Node node) {/** If status is negative (i.e., possibly needing signal) try* to clear in anticipation of signalling. It is OK if this* fails or if status is changed by waiting thread.*/int ws = node.waitStatus;if (ws < 0)// 重置头结点的状态waitStatuscompareAndSetWaitStatus(node, ws, 0);/** Thread to unpark is held in successor, which is normally* just the next node. But if cancelled or apparently null,* traverse backwards from tail to find the actual* non-cancelled successor.*/// 获取头结点的下一个节点Node s = node.next;// s.waitStatus > 0 为取消状态 ,结点为空且被取消if (s == null || s.waitStatus > 0) {s = null;// 获取队列里没有cancel的最前面的节点for (Node t = tail; t != null && t != node; t = t.prev)if (t.waitStatus <= 0)s = t;}// 如果节点s不为null,则获得锁if (s != null)LockSupport.unpark(s.thread);}
锁的释放这个还是很简单。
总结
这个源码的最好阅读方式是结合例子去自己一步步跟代码,把每一个步骤写在纸上,尝试一两遍你就会有非常清晰的认识。
大家多给些意见,写之前我信心满满觉得能写的让大家看懂,写完之后我觉得一坨屎。



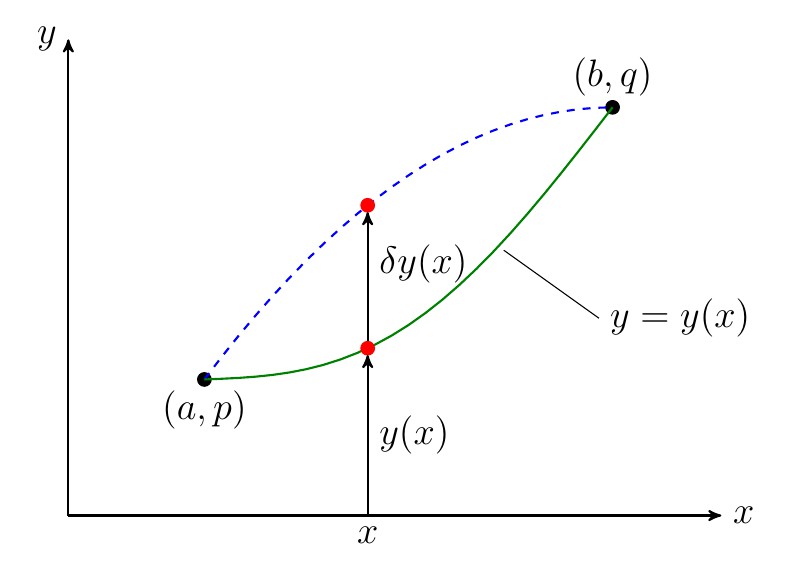
![[变分法介绍]优美的旋轮线:最速下降线问题,通过费马光学原理的初等证明](https://img-blog.csdnimg.cn/20200621210611999.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MzcwMDczMg==,size_16,color_FFFFFF,t_70#pic_center)