在介绍变分贝叶斯之前，首先以这篇博客介绍下大名鼎鼎的变分法。 参考资料主要是知乎的文章与维基百科。

变分就是函数的微分。

回顾一下传统的函数优化问题。 对于${\min }_{x}f(x)$这样的优化问题，求取最优的$x$的做法常用一阶条件，即：
$$\frac{\partial f}{\partial x^{\star }}=0$$
对应的物理意义是从该点出发的任何变化方向都无法让函数值进一步下降，也即:
$$f(x^{\star })\le f(x^{\star }+ϵdx)$$
因此，这也是最优的$x^{\star }$的必要条件， 容易通过反证法求证。如果将这个方法称为变量求最优解的微分法， 那变函数求最优解的类似方法就是变分法。 具体而言， 此时变量$x$成了给定的东西，我们要通过优化函数来最小化函数值， 也即${\min }_{f}g(f(x))$。 $g$就是以函数为变量的目标函数， 而函数的变化量就是变分。 我们通过一个经典的例子来进行阐释。

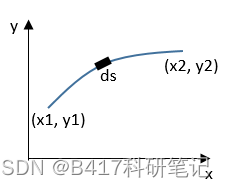
如上图所示， 存在函数$y=f(x)$。 对应上图 $y1=f(x_1)$, $y_2=f(x_2)$。我们的问题是寻找给定的$(x1,y1)$和$(x2,y2)$间的最短距离所对应的$f$函数。 通过小学知识我们知道，结论是两点之间线段最短。现在我们通过变分法论证这一点， 也即$f$函数是一个一次线性函数。

首先，我们可以将$(x1,y1)$和$(x2,y2)$间的距离显示地写出，作为我们的目标函数。 具体地， 我们取线上的一小段微元$ds$ （参考上图)， 根据勾股定理显然有 （注意是$d{y}^2$不是$d^{2}y$）：
$$d{s}^2=d{x}^2+d{y}^2=\left[1+{\left(y^{\prime }\right)}^2\right]d{x}^2$$
因此$ds=\sqrt{1+{\left(y^{\prime }\right)}^2}dx$，总路径长度可写为：

$$A[f]={\int }_{x_1}^{x_2}\sqrt{1+{\left[f^{\prime }(x)\right]}^2}dx$$

此时路径长度为函数$f$的函数。 类似于一阶条件， 假设$f_0$是能达到局部最小的函数，那么有：
$$A\left[f_0\right]\le A\left[f_0+ϵf_1\right]$$
其中$f_1$是以$x1$和$x2$为端点的任意函数，$ϵ$代表一个极小值。类似地，这就要求对于任意$f_1$，当$ϵ\to 0$时， $A\left[f_0+ϵf_1\right]$对$ϵ$的导数为$0$：（对于给定的$f_1$，$A\left[f_0+ϵf_1\right]$是$ϵ$的函数）

$${\frac{d}{dϵ}{\int }_{x_1}^{x_2}\sqrt{1+{\left[f_0^{\prime }(x)+ϵf_1^{\prime }(x)\right]}^2}dx|}_{ϵ=0}={{\int }_{x_1}^{x_2}\frac{\left(f_0^{\prime }(x)+ϵf_1^{\prime }(x)\right)f_1^{\prime }(x)}{\sqrt{1+{\left[f_0^{\prime }(x)+ϵf_1^{\prime }(x)\right]}^2}}|}_{ϵ=0}dx={\int }_{x_1}^{x_2}\frac{f_0^{\prime }(x)f_1^{\prime }(x)}{\sqrt{1+{\left[f_0^{\prime }(x)\right]}^2}}dx=0$$

此处可以使用分部积分法： $\int udv=uv-\int vdu$。令$v=f_1(x)$, $u=\frac{f_0^{\prime }(x)}{\sqrt{1+{\left[f_0^{\prime }(x)\right]}^2}}$，得到：
$${\int }_{x_1}^{x_2}{f}_1(x)\frac{d}{dx}\left[\frac{f_0^{\prime }(x)}{\sqrt{1+{\left[f_0^{\prime }(x)\right]}^2}}\right]dx=0$$
这里使用了条件$f_1(x1)=f_1(x2)=0$。 由于对于任意$f_1$都要有此结论，因此:
$$\frac{d}{dx}\left[\frac{f_0^{\prime }(x)}{\sqrt{1+{\left[f_0^{\prime }(x)\right]}^2}}\right]=0$$
化简终可得到：
$$\frac{d^2{f}_0}{d{x}^2}=0$$
也即，$f(x)$为直线。

而对于更普遍的情况， 一般函数的函数都可以写为如下形式:

$$A[f]={\int }_{x_1}^{x_2}L\left(x,f,f^{\prime }\right)dx$$
即变量为$x$，函数和函数的一阶导。此时，根据类似的推导，可以得到最优解需要满足条件：

$$-\frac{d}{dx}\frac{\partial L}{\partial f^{\prime }}+\frac{\partial L}{\partial f}=0$$
这也被称为欧拉-拉格朗日方程， 为极值的必要条件。而由此求取极值的方法也即变分法。