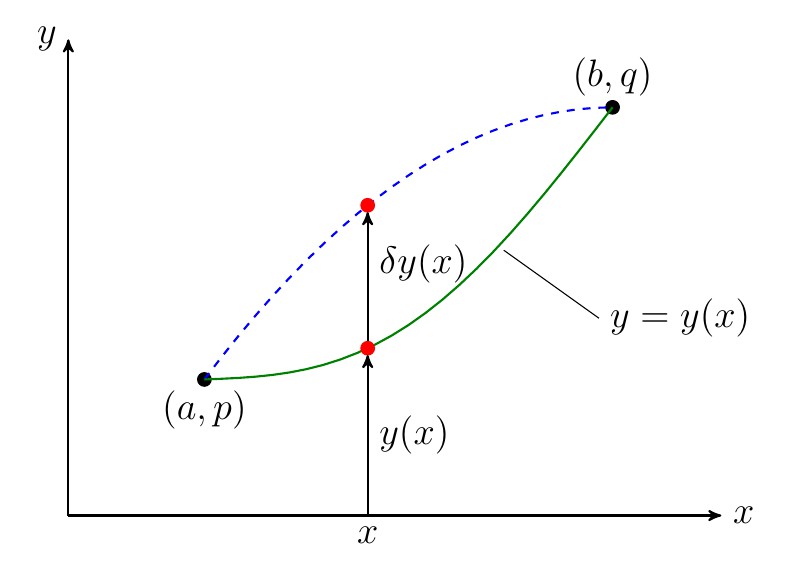
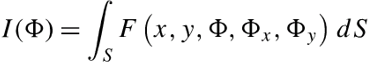mathematica求解最小面积旋转曲面
做你没做过的事叫成长,做你不愿做做的事叫改变,做你不敢做的事叫突破。—— 巴菲特
问题描述:
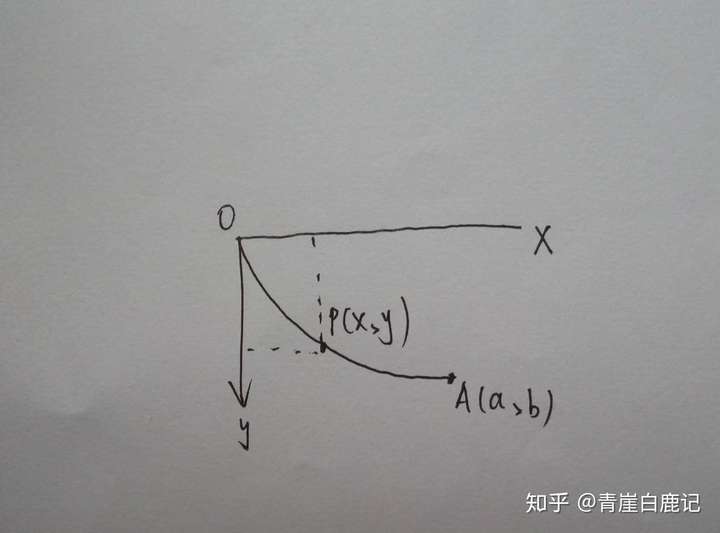
在一条直线的同一侧有两个已知点,试找出一条连接这两点的曲线,使这条曲线绕直线旋转所得的曲面面积最小。
- 插入等n个等分节点,中间n-1个节点y值用未知数表示。用类似于求最速降线的方法,在每一个小区间上进行线性插值。 利用旋转曲面表面积公式求得每一段区间上圆台侧面积,加和求极小值,以求得未知的y值。代码如下:
(*分段线性插值方法求最小旋转曲面面积*)
area[{a1_, h1_}, {a2_, h2_}] := Block[{S, R, r, L}, R = h1; r = h2;L = Sqrt[(h2 - h1)^2 + (a2 - a1)^2];S = Pi*(R + r)*L;S];(*输入两点,求过这两点和x轴围城的梯形面积*)
x0 = 0; d0 = 9;
xn = 7; dn = 2;(*输入两点坐标*)
n = 30; dx = (xn - x0)/n;
partitionPs = Table[{x0 + dx*i, y[i]}, {i, 1, n - 1}];
PrependTo[partitionPs, {x0, d0}];
AppendTo[partitionPs, {xn, dn}];(*表示出划分成n份后每点的坐标*)
partS = Table[area[partitionPs[[i - 1]], partitionPs[[i]]], {i, 2, n + 1}];(*求每一小块梯形的面积*)
S = Total[partS];(*将每一小块梯形面积求和*)
initialvalue = Table[{y[i], d0 + i*(dn - d0/n)}, {i, 1, n - 1}];(*两点间的线性划分作为初值*)
result = FindMinimum[{S, Table[y[i] > 0, {i, 1, n - 1}]}, initialvalue];(*求使总面积为极小值的未知数y*)
pic1 = ListPlot[partitionPs /. result[[2]], PlotRange -> Full, Joined -> True]
minarea = S /. result[[2]](*最小面积*)
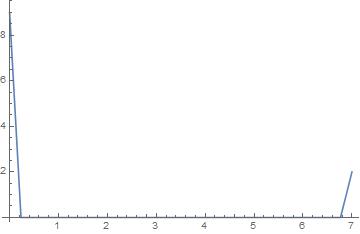
但是我们在调整两点坐标时,发现出现了如下情况:
我们对原来的函数没有任何限制,出现这种情况是自然而然的。从这里看到,函数图像在 C1 上不连续。容易想到,我们可以利用分段艾米特插值或者样条函数插值避免这种情况的发生。
2. 做分段样条插值保证 C2 连续
- 由于mathematica自带的样条插值不能进行符号运算,我们只能自己构造样条插值函数
- 三对角矩阵可以用利用稀疏矩阵函数SparArray来产生
- 及时清除变量值,以保证下一次运行不出错。如有必要,需重启软件,初始化内核
- 由于mathematica自带的积分函数计算速度太慢,分段一多,几乎无法等待,所以可以考虑使用辛普森公式来近似估计每一段旋转曲面面积,以求加和最小
(*三次样条插值方法求最小旋转曲面侧面积*)
Clear[lambda, mu, X, M, y, pics, area];(*清除变量*)
n = 3;(*设置分段数*)
x[0] = 0;
y[0] = 8;
x[n] = 5;
y[n] = 7;(*输入两点坐标*)
pics = Array[f, n]; pics2 = Array[0, n];(*定义数组,用于存图*)
h = (x[n] - x[0])/n;
d[0] = 0; d[n] = 0;(*样条插值三对角方程右端项在补充自然边界条件是置为0*)
lambda[0] = 0; mu[n] = 0;(*三对角矩阵中的lambda0和mu0为0,其余都为1/2*)
Table[x[i] = x[0] + i*h, {i, 1, n - 1}];(*等距划分x轴*)
X = SparseArray[{{i_, i_} -> 2, {i_, j_} /; Abs[i - j] == 1 && i != 1 && i != n + 1 -> 1/2}, {n + 1, n + 1}];(*使用稀疏矩阵生成三对角矩阵*)
MatrixForm[X](*三对角矩阵矩阵形式展示*)
Table[d[i] = 3/h^2*(y[i + 1] - 2*y[i] + y[i - 1]), {i, 1, n - 1}];(*循环生成含未知数的d*)
L = LinearSolve[X, Table[d[i], {i, 0, n}]];(*求解方程Xx=d*)
Table[M[i] = L[[i + 1]], {i, 0, n}];(*求得弯矩M,即各分点的二阶导数值*)
Table[A[i] = (y[i + 1] - y[i])/h - h/6*(M[i + 1] - M[i]);B[i] = y[i] - M[i]*h^2/6;S[i + 1] = 1/(6*h)*(x - x[i])^3*M[i + 1] - 1/(6*h)*(x - x[i + 1])^3*M[i] + A[i]*(x - x[i]) + B[i], {i, 0, n - 1}];(*将弯矩M代入公式,求得每一小段上的样条插值函数*)
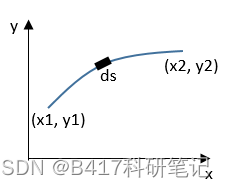
area = Sum[2 Pi*h/6*(((S[i]*Sqrt[1 + D[S[i], x]^2]) /. x -> x[i - 1]) + ((S[i]*Sqrt[1 + D[S[i], x]^2]) /. x -> x[i]) + ((4*S[i]*Sqrt[1 + D[S[i], x]^2]) /. x -> (x[i] - h/2))), {i, 1, n}];
(*由旋转体面积公式求得侧面积*)
yy0 = Table[{y[i], y[0] + i*(y[n] - y[0])/n}, {i, 1, n - 1}];(*求极值的初值*)
result = FindMinimum[{area, Table[y[i] > 0, {i, 1, n - 1}]}, yy0];(*求解极值点*)
Table[pics[[i]] = Plot[S[i] /. result[[2]], {x, x[i - 1], x[i]}], {i, 1, n}];
Show[pics, PlotRange -> All](*绘图*)
Table[pics2[[i]] = RevolutionPlot3D[S[i] /. result[[2]], {x, x[i - 1], x[i]}, RevolutionAxis -> "X"], {i, 1, n}];
Show[pics2, PlotRange -> Automatic](*绘图*)
result(*求得最小面积*)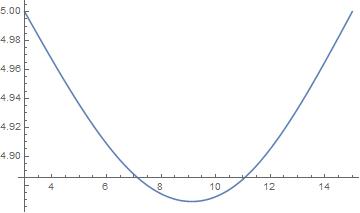
3. Mathematica变分法求解最小面积旋转曲面
理论证明,最小旋转曲面函数是双曲余弦函数:
y=Acosh(x−BA)
那么,理论上我们只要将两点带入反解出A、B的值即可。求解非线性方程组 f(x)=0 可以转化为求 fT(x)f(x) 最小值的问题。使用RevolutionPlot3D命令可画出旋转图形。
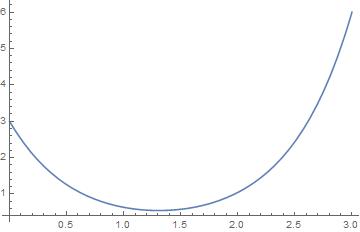
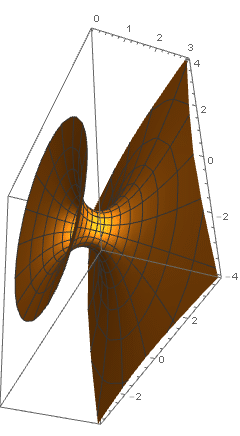
变分法代码
(*变分法求最小旋转曲面面积*)
ch[x_, y_] := Cosh[(x - B)/A]*A - y;(*定义一般的最小面积双曲余弦曲线*)
x0 = 0; y0 = 8;
xn = 5; yn = 7;(*给定两点坐标*)
ContourPlot[{ch[x0, y0] == 0, ch[xn, yn] == 0}, {A, -30, 30}, {B, -30,30}](*绘制将AB视为变远时的两点代入的图像,观察交点*)
psbsol = NSolve[{ch[x0, y0] == 0, ch[xn, yn] == 0}, {A, B}, Reals];
(*当图像有交点时,表明方程组有解,可用Nsolve求解非线性方程组,速度较慢*)
(*result=NMinimize[ch[x0,y0]^2+ch[xn,yn]^2,{A,B}]
FindRoot[{ch[x0,y0]\[Equal]0,ch[xn,yn]\[Equal]0},{A,1},{B,1}] \
适当改用这两种方式求解最优值,可提高速度*)
If[psbsol != {},(*讨论当方程组解集非空的情况*)area = {}; lines = {};For[i = 1, i <= Length[psbsol], i++, temp = (Cosh[(x - B)/A]*A) /. psbsol[[i]]; AppendTo[lines, temp];AppendTo[area, 2*Pi*NIntegrate[temp*Sqrt[1 + D[temp, x]^2], {x, x0, xn}]]];(*分别求方程组两个解对应的解曲线和旋转面积*)index = Ordering[area][[1]];(*求最小旋转面积在所有解集中的位置*)minarea = area[[index]];(*最小旋转面积*)minline = lines[[index]];(*最小旋转曲线*)pic1 = Plot[minline, {x, x0, xn}];pic2 = RevolutionPlot3D[minline, {x, x0, xn}, RevolutionAxis -> "X"];(*绘图*)]
If[psbsol == {},(*当图像无交点时表明原方程组无解,此时用另外的方法得到结果*)result = NMinimize[ch[x0, y0]^2 + ch[xn, yn]^2, {A, B}];(*求极值作为最小值*)minline = Cosh[(x - B)/A]*A /. result[[2]];pic1 = Plot[minline, {x, x0, xn}];pic2 = RevolutionPlot3D[minline, {x, x0, xn}, RevolutionAxis -> "X"];minarea = 2*Pi*NIntegrate[minline*Sqrt[1 + D[minline, x]^2], {x, x0, xn}]]
minarea
minline
Show[pic1]
Show[pic2]
连蒙带猜,学会折腾 —— 赵永成
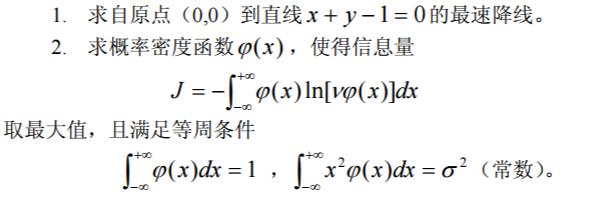

![[变分法介绍]优美的旋轮线:最速下降线问题,通过费马光学原理的初等证明](https://img-blog.csdnimg.cn/20200621210611999.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MzcwMDczMg==,size_16,color_FFFFFF,t_70#pic_center)