泛函与泛函极值问题

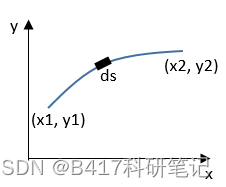
平面内两点A，B，连接两点之间的曲线有很多种方式。分别用函数$f_i(x)$来表示。对于给定的曲线$f_i(x)$, 那么两点之间连线的长度可以表示为
$$J(f_i(x))=\underset{A}{\overset{B}{\int }}\sqrt{1+f_i^{\prime }(x{)}^2}dx$$
这里$J$是函数$f$的函数，又叫泛函。通过求$J$的极值，求得对应的$f(x)$，就是泛函的极值问题。求泛函极值问题常用的方法就是变分法。

变分法和欧拉-拉格朗日方程

考虑泛函(functional)常见形式
$$J=\underset{x_1}{\overset{x_2}{\int }}F(x,y(x),y^{\prime }(x))dx$$
其中

• $x_1$,$x_2$是常数；
• $y(x)$二阶连续可微函数；
• $y^{\prime }(x)=dy/dx$;
• $F(x,y(x),y^{\prime }(x))$是关于变量$x$,$y$,$y^{\prime }$的二阶连续可微函数。

假如泛函$J[y]$在$f$处取得局部极小值，对于任意函数$\eta (x)$, 有一阶导数且在$\eta (x_1)=\eta (x_2)=0$, 对于趋近于0的任意小的数$\epsilon$，有：
$$J[f]\le J[f+\epsilon \eta ]$$
其中，$\epsilon \eta$就是函数$f$的变分，用$\delta f$来表示。
用$f+\epsilon \eta$替换泛函$J[y]$中的$y$，结果就是$\epsilon$的一个函数：
$$\Phi (\epsilon )=J[f+\epsilon \eta ]$$
因为函数$J$在$f$处取得极小值，所以函数$\Phi (\epsilon )$在$\epsilon =0$处取得极小值，因此，
$${\Phi }^{\prime }(0)\equiv \frac{d\Phi }{d\epsilon }{|}_{\epsilon =0}={\int }_{x_1}^{x_2}\frac{dF}{d\epsilon }{|}_{\epsilon =0}dx=0$$
对泛函$F(x,y,y^{\prime })$求全微分，其中$y=f+\epsilon$，$y^{\prime }=f^{\prime }+\epsilon {\eta }^{\prime }$都是$\epsilon$的函数，但是$x$不是(即，$\frac{dx}{d\epsilon }=0$)，所以有：
$$\frac{dF}{d\epsilon }=\frac{\partial F}{\partial y}\frac{dy}{d\epsilon }+\frac{\partial F}{\partial y^{\prime }}\frac{d{y}^{\prime }}{d\epsilon }$$
因为$\frac{dy}{d\epsilon }=\eta$, $\frac{d{y}^{\prime }}{d\epsilon }={\eta }^{\prime }$，所以有：
$$\frac{dF}{d\epsilon }=\frac{\partial F}{\partial y}\eta +\frac{\partial F}{\partial y^{\prime }}{\eta }^{\prime }$$
因此
$$\begin{array}{rl}{\int }_{x_1}^{x_2}\frac{dF}{d\epsilon }{|}_{\epsilon =0}dx& ={\int }_{x_1}^{x_2}(\frac{\partial F}{\partial f}\eta +\frac{\partial F}{\partial f^{\prime }}{\eta }^{\prime })dx\\ & ={\int }_{x_1}^{x_2}(\frac{\partial F}{\partial f}\eta +\frac{d}{dx}(\frac{\partial F}{\partial f^{\prime }}\eta )-\eta \frac{d}{dx}\frac{\partial F}{\partial f^{\prime }})dx(分部积分)\\ & ={\int }_{x_1}^{x_2}(\frac{\partial F}{\partial f}\eta -\eta \frac{d}{dx}\frac{\partial F}{\partial f^{\prime }})dx+\frac{\partial F}{\partial f^{\prime }}\eta {|}_{x_1}^{x_2}\end{array}$$
当$\epsilon =0$时，$F[x,y,y^{\prime }]\to F[x,f,f^{\prime }]$。因为$\eta (x_1)=\eta (x_2)=0$，且公式左边等于0，所以有：
$${\int }_{x_1}^{x_2}\eta (x)(\frac{\partial F}{\partial f}-\frac{d}{dx}\frac{\partial F}{\partial f^{\prime }})dx=0$$
根据变分法基本定理，知道：
$$\frac{\partial F}{\partial f}-\frac{d}{dx}\frac{\partial F}{\partial f^{\prime }}=0$$
这个公式即为欧拉-朗格朗日方程（ Euler-Lagrange）。欧拉-拉格朗日方程还可以推广至多元和高阶，在偏微分方程和微分几何领域有广泛的应用前景。

变分法典型应用

最短距离问题

针对一开始提出的最短距离问题，其泛函表示形式为：
$$J(f(x))=\underset{A}{\overset{B}{\int }}\sqrt{1+f^{\prime }(x{)}^2}dx$$
即
$$F(x,y,y^{\prime })=\sqrt{1+f^{\prime }(x{)}^2}$$
$$\frac{\partial F}{\partial f}=0$$
$$\frac{\partial F}{\partial f^{\prime }}=\frac{f^{\prime }(x)}{\sqrt{1+f^{\prime }(x{)}^2}}$$
$$\frac{d}{dx}\frac{\partial F}{\partial f^{\prime }}=f^{\prime \prime }(x)(1+f^{\prime }(x{)}^2{)}^{-\frac{3}{2}}$$
根据欧拉公式，得：$$f^{\prime \prime }(x)=0$$
所以：
$$f^{\prime }(x)=a$$
$$f(x)=ax+b$$
其中$a,b$为与起始点相关的常数。即两点之间直线最短。