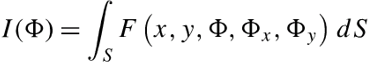变分法：在图像处理中的应用（一）

前言

最近学习稠密重建的相关知识，发现变分法通常作为一个平滑的正则项出现在残差平方和的损失函数中。而图像处理中又经常出现这类最小损失函数的优化问题，如图像分割、稠密光流、稠密重建等等，这些优化问题中都有可能涉及到变分法。因此，我想系统记录下学习过程：变分法是什么？全变分正则项有何含义？加了变分正则项的损失函数如何求解？等等。本系列应该会有三章：

第一章讲数学基础：泛函极值和变分法
第二章讲变分法在图像去噪上的应用
第三章讲变分法在稠密重建上的应用

变分法基础

变分法求解的过程大致为：首先从问题出发构建能量泛函及约束条件，然后构建对应的 Euler-Lagrange 偏微分方程，最后在初值条件下求解偏微分方程的数值解。后续小节将按照这个思路对变分法求极值的原理进行梳理。目前，网上变分法资料比较多，我仅仅是将其他资料进行一个结合和梳理，感兴趣的小伙伴可以阅读参考文献列表。

趣事

最速下降问题是伽利略在 1630 年提出的：让一个物体从静止开始在一个光滑的轨道上从高处开始下滑，问最快到达低处的轨道形状应该是什么样的？如下图所示，图片来源 wiki。
在这里插入图片描述
大家都知道两点之间直线最短，但从图中可以看出，最短的路径并不是最快抵达的。伽利略没有找到问题的正确解，只证明了圆弧的下降速度比直线快。
时间来到微积分学快速发展的那个黄金年代，Johann Bernoulli (伯努利家族) 于 1696 年在《教师学报》上就最速曲线问题向全欧洲的数学家提出点名挑战，规定 6 个月后公布如何求解答案。在提出这个有趣挑战的同一年，牛顿、莱布尼茨、洛必达、Johann Bernoulli 和 Jacob Bernoulli 都得到了同一个结论。再后来，欧拉（1744年）和拉格朗日（1760年）对这类问题进行了推广并得到了一个求解的通用方程：Euler-Lagrange Equation。
在看到这一连串大佬名字以后，相信大家心理都不由得感叹了一下。接下来，我们也将借助这个问题对变分法涉及到的数学基础进行整理和推导。

从最短路径到变分求解

在求解上述最速下降问题之前，我们先从另一个熟知的最短路径问题开始，即找到使得从 A 点到 B 点之间路径最短的曲线方程 $y (x)$ 。
假设两个端点的坐标分别为 $\left(a,p\right)$ 和 $\left(b,q\right)$ ，连接这两个点的任意曲线方程 $y = y (x)$ 都满足如下边界条件：
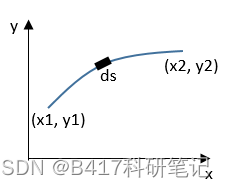
$\quad y(b)=q$ 为了计算曲线 $y (x)$ 的长度，我们可以采用积分的方法，将曲线分成很多微小线段，将所有线段进行累积来计算总长度：
$\begin{aligned} \mathrm{d}s &= \sqrt{\mathrm{d}x^2 + \mathrm{d}y^2} = \sqrt{1 + \left(\frac{\mathrm{d}y}{\mathrm{d}x}\right)^2} \mathrm{d}x = \sqrt{1+y^{\prime 2}} \mathrm{d}x \\ \ S &= \int_a^b \sqrt{1+y^{\prime 2}} \mathrm{d}x \qquad\qquad(1) \end{aligned}$ 因此，最短路径对应的曲线方程 $y (x)$ 应使得 $S$ 取极小值。通常，我们是估计一个变量 $x$ 使得某个函数 $y (x)$ 取极值，求解的方法是令一阶导等于 0，因此求方程 $y^{\prime}(x) =0$ 就可以得到 $x$ 。但这里问题不一样，这里是求一个函数 $y (x)$ 使得 $S$ 取极值，需要求解的是一个什么样的函数 $y (x)$ 而不是变量 $x$ 。如下图所示 [参考资料 1]，求解的量不是 $x$ 而是函数 $y (x)$ ，函数的微小变化 $\delta y(x)$ 称之为函数 $y (x)$ 的变分。注意，函数的微分 $\mathrm{d}y$ 是变量 $x$ 的微小变化导致的函数变化，而变分是函数自身发生的微小变化，跟自变量 $x$ 的变化没有关系。

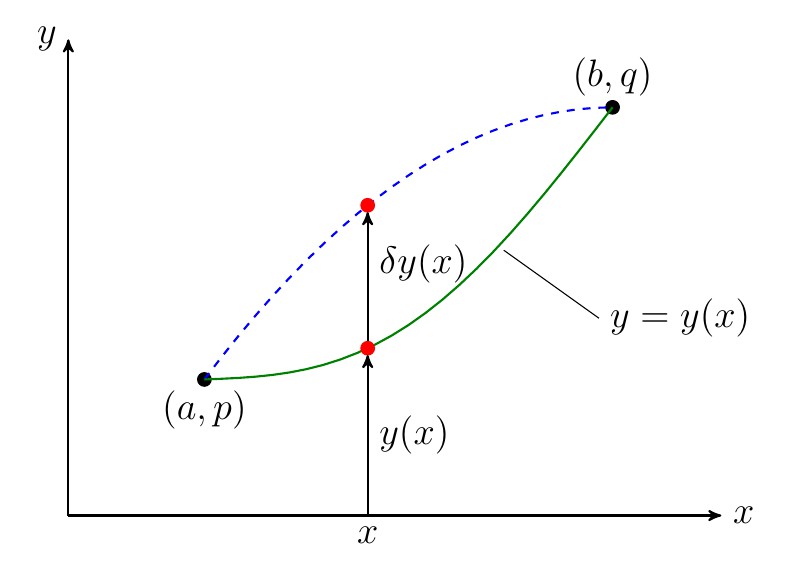
现在，我们将这个问题进行一般化处理，假设我们构建的积分函数是如下形式：
$\int_a^b F\left(x,y,y^{\prime}\right)\mathrm{d}x$ 所谓泛函是指 $C$ 的数值依赖函数 $y (x)$ 的变化而变化， $C$ 和 $y (x)$ 之间的这种依赖关系就称为泛函关系。其中 $F$ 是关于 $x$ , $y (x)$ 以及一阶导 $y^{\prime}(x)$ 的函数。

假设存在 $y (x)$ 使得 $C$ 取最小值，并且一阶导数存在。我们给曲线加一个变分扰动，当扰动接近 0 时，函数 $C$ 的变化也接近 0 ：
$\begin{aligned} \delta C &= C(y+\delta y ) - C(y) \\ &=\int_a^b\left[ F\left(x,y+\delta y,y^{\prime}+\delta y^{\prime} \right)-F\left(x,y,y^{\prime}\right) \right] \mathrm{d}x \end{aligned}$ 根据微分和变分的定义，大家可以快速的证明微分运算符和变分运算符两者可以互换顺序，具体推导见参考资料 5：
$\mathrm{d}(\delta y ) = \delta ( \mathrm{d}y)$ 对函数 $F$ 进行泰勒展开有：
$\begin{aligned} F(x, y + \delta y, y^{\prime} + \delta y^{\prime}) &= F(x,y,y^{\prime})+\frac{\partial F(x,y,y^{\prime})}{\partial y}\delta y + \frac{\partial F(x,y,y^{\prime})}{\partial y^{\prime}}\delta y^{\prime} \\ &=F(x,y,y^{\prime})+\frac{\partial F(x,y,y^{\prime})}{\partial y}\delta y + \frac{\partial F(x,y,y^{\prime})}{\partial y^{\prime}}(\delta y)^{\prime} \end{aligned}$ 所以有：
$\delta C = \int_a^b \left( \frac{\partial F(x,y,y^{\prime})}{\partial y}\delta y + \frac{\partial F(x,y,y^{\prime})}{\partial y^{\prime}}(\delta y)^{\prime} \right) \mathrm{d}x \qquad\qquad(2)$ 为了方便书写，后续我们将 $F(x,y,y^{\prime})$ 用 $F$ 替代，考虑到分部积分法有：
$\int u \mathrm{d}v = uv - \int v \mathrm{d}u$ 由此将公式 (2) 中的第二部分利用分部积分公式可得：
$\begin{aligned} \int_a^b \frac{\partial F}{\partial y^{\prime} }(\delta y)^{\prime} \mathrm{d}x &= \int_a^b \frac{\partial F}{\partial y^{\prime} } \mathrm{d}(\delta y) \\ &= \frac{\partial F}{\partial y^{\prime} } \delta y |_a^b - \int_a^b \delta y \frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{\partial F}{\partial y^{\prime} }\right) \mathrm{d}x \end{aligned}$ 考虑到所有的曲线方程都穿过端点 $a, b$ ，即在端点处函数不会变化，有 $\delta y(a) = \delta y(b) = 0$ ，所以分部积分的第一项等于 $0$ ，将剩余的部分带入公式 (2) 有：
$\delta C = \int_a^b \left( \frac{\partial F}{\partial y} - \frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{\partial F}{\partial y^{\prime}} \right) \right) \delta y \mathrm{d}x$ 跟一阶导等于 0 的原理类似， $C$ 存在极值时，对任意微小变化的 $\delta y(x)$ 都必须有 $\delta C = 0$ ，由此得到：
$\frac{\partial F}{\partial y} - \frac{\mathrm{d}}{\mathrm{d}x}\frac{\partial F}{\partial y^{\prime}} = 0 \qquad\qquad(3)$ 方程 (3) 就是大名鼎鼎的 Euler-Lagrange 方程，有了这个偏微分方程再加上一些边界条件，通常就可以确定函数 $y (x)$ 。

引理：若函数表达式 $F(x,y,y^{\prime})=F(y,y^{\prime})$ 不显式含有 $x$ ，则 Euler-Lagrange 方程可以改写为：
$\frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{\partial F}{\partial y^{\prime} } y^{\prime} - F \right)=0 \qquad\qquad(4)$ 证明：
$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d} x}\left(\frac{\partial F}{\partial y^{\prime}} y^{\prime}\right) &=\frac{\mathrm{d}}{\mathrm{d} x}\left(\frac{\partial F}{\partial y^{\prime}}\right) y^{\prime}+\frac{\partial F}{\partial y^{\prime}} y^{\prime \prime} \\ \frac{\mathrm{d}}{\mathrm{d} x} F &=\frac{\partial F}{\partial x}+\frac{\partial F}{\partial y} \cdot \frac{\partial y}{\partial x}+\frac{\partial F}{\partial y^{\prime}} \cdot \frac{\partial y^{\prime}}{\partial x} \\ &=\frac{\partial F}{\partial y} y^{\prime}+\frac{\partial F}{\partial y^{\prime}} y^{\prime \prime} \\ \therefore \frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{\partial F}{\partial y^{\prime} } y^{\prime} - F \right) &= \frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{\partial F}{\partial y^{\prime} } \right) y^{\prime} - \frac{\partial F}{\partial y} y^{\prime}\\ &=\left( \color{Red} \frac{\mathrm{d}}{\mathrm{d} x}\left(\frac{\partial F}{\partial y^{\prime}}\right)-\frac{\partial F}{\partial y}\right) y^{\prime} \\ &=0 \end{aligned}$

再看最短路径和最速下降问题

求解最短路径

方程 (1) 的最短路径问题中，我们希望 $S$ 取到最小值，且已有了 $F(y,y^{\prime}) = \sqrt{1+y^{\prime}}$ ，利用 Euler-Lagrange 方程来求解函数 $y (x)$ 。计算偏导数并写出 Euler-Lagrange 方程：
$\begin{aligned} \frac{\partial F}{\partial y}=0, \quad \frac{\partial F}{\partial y^{\prime} } = \frac{y^{\prime}}{\sqrt{1+y^{\prime 2}}} \\ \xrightarrow[]{\text{Euler-Lagrange}} \frac{\mathrm{d}}{\mathrm{d} x}\left(\frac{y^{\prime}}{\sqrt{1+y^{\prime 2}}} \right)=0 \end{aligned}$ 上面 Euler-Lagrange 得到一个关于 $x$ 的导数恒等于 0 的微分方程，意味着括号里为常数，从而知道 $y^{\prime}$ 必然也是一个常数，由此 $y (x)$ 应该是如下形式：
$y = k x + c$

求解最速下降

回到本文最开始的历史趣事，现在我们来求解最速下降的曲线方程。假设轨道起始点和终点坐标分别为 $(0, 0)$ 和 $(a, b)$ ，并且构建一个求解的坐标系，其 $y$ 轴为垂直地面向下， $x$ 轴方向为水平。根据能量守恒定律，我们可以计算出小球沿着轨道滑到 $(x, y)$ 处时的速度关系为：
$\frac{1}{2} m v^2 = mgv \longrightarrow v=\sqrt{2gy}$ 同时，根据速度的定义有：
$\frac{\mathrm{d}s}{\mathrm{d}t} = \sqrt{1+y^{\prime}}\frac{\mathrm{d} x}{\mathrm{d} t}$ 由此可得到：
$\mathrm{d}t=\sqrt{\frac{1+y^{\prime}}{2gy}}\mathrm{d}x$ 将时间进行积分，就能得到总时间的泛函关系：
$\frac{1}{\sqrt{2g}}\int_0^a\sqrt{\frac{1+y^{\prime}}{y}}\mathrm{d}x$ 又到了熟悉的套路时间，我们可以先求相应的偏导数再构建 Euler-Lagrange 方程最后求解偏微分方程得到 $y (x)$ 。
这里我们直接给出 Euler-Lagrange 方程：
$\frac{1}{2 y} \sqrt{\frac{1+y^{\prime 2}}{y}}+\frac{\mathrm{d}}{\mathrm{d} x} \frac{y^{\prime}}{\sqrt{y\left(1+y^{\prime 2}\right)}}=0$ 再借用引理得到：
$\frac{\mathrm{d}}{\mathrm{d} x}\left(\frac{y^{\prime2}}{\sqrt{y\left(1+y^{\prime2}\right)}}-\sqrt{\frac{1+y^{\prime 2}}{y}}\right)=0 \Longleftrightarrow \frac{\mathrm{d}}{\mathrm{d} x} \frac{1}{\sqrt{y\left(1+y^{\prime 2}\right)}}=0$
令 $y^{\prime}=cot\frac{\theta}{2}$ ，可以得到 $x, y$ 的参数方程：
$\left\{\begin{array}{l} x=\frac{C}{2}(\theta-\sin \theta) \\ y=\frac{C}{2}(1-\cos \theta) \end{array}\right.$
其中 C 为常数。上述方程为摆线方程，对应一个圆滚动时候圆周上一个定点的轨迹。上述微分方程的求解，我没有实际验证，水平不行 -_-!