简述变分法在泛函极值问题中的应用

article/2025/10/7 19:42:02

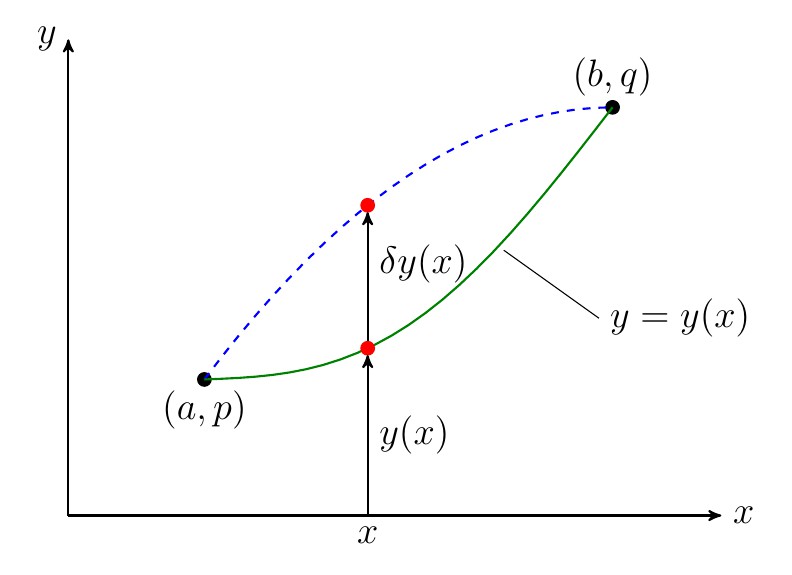
此文主要有两部分内容，一部分是泛函的一些基本概念；第二部分是变分法在研究泛函极值问题中的应用。

第一部分泛函

泛函是函数概念的一种扩充，函数描述的是从数到数的对应关系，从自变量到因变量的一种对应关系；而泛函描述的是函数到数的一种映射关系。

定义：对于某一类函数集合中的每一个函数 $y(x)$ ，都存在一个确定的数 $J$ 与之对应，那么就称 $J$ 为依赖于函数 $y(x)$ 的泛函，记为

$J=J\left[ y(x) \right]$

简记为J，相应的自变量函数 $y(x)$ 称为宗量。

注意：宗量 $y(x)$ 是某一特定函数的整体，而不是对应于某一自变量 $x$ 的函数值；宗量 $y(x)$ 属于的函数类称为容许函数类或者容许函数空间。

线性泛函满足可叠加性和齐次性。

泛函极值问题则是，在容许函数类中求使得泛函达到极值的函数。

第二部分变分法在研究泛函极值问题中的应用

在介绍变分法之前，我们先给出函数微分的定义，如下

若函数 $f(x)$ 具有连续的导数，则它的增量可以表示如下

$\Delta y=f(x+\Delta x)-f(x)=\dot{f}(x)\Delta x+r(x,\Delta x)$

其中 $\dot{f}(x)\Delta x$ 是 $\Delta x$ 的线性函数； $r(x,\Delta x)$ 是 $\Delta x$ 的高阶无穷小量。

当 $\Delta x$ 充分小时， $\dot{f}(x)\Delta x$ 起主要作用， $\dot{f}(x)\Delta x$ 为函数增量的线性主部，也称为函数的微分，记为

$dy=\dot{f}(x)dx$ 。

泛函宗量的变分是指同一函数类中两个函数之差，记为

$\delta y(x)=y(s)-y_0(x)$ 。

若连续泛函 $J\left[y(x) \right ]$ 的增量可以表示为

$\Delta J\left[y(x) \right ]=J\left[y(x)+\delta y(x) \right ]-J\left[y(x) \right ]=L(y(x),\delta y(x))+r(y(x),\delta y(x))$

其中 $L(y(x),\delta y(x))$ 为 $\delta y(x)$ 的线性连续泛函， $r(y(x),\delta y(x))$ 为 $\delta y(x)$ 的高阶无穷小。记为

$\delta J=L(y(x),\delta y(x))$ 。

上式可类比函数微分是函数增量的线性主部一样，泛函的变分是泛函增量的线性主部，所以泛函的变分也称为泛函的微分。

引理1：泛函 $J[ y(x)]$ 的变分为

$\delta J=\frac{\partial}{\partial \alpha}J[y(x)+\alpha\delta y(x)]\left|_{\alpha=0}\right.$ 。

定理1：若可微泛函在 $y_0(x)$ 上达到极小（极大）值，则在 $y=y_0(x)$ 上有

$\delta J=0$ 。

泛函的变分实际上就是关于其宗量变分 $\delta y(x)$ 的线性连续泛函，因此，可以通过求泛函对其所有宗量的一阶偏微分得到泛函的变分。

泛函 $J[y_1(x),y_2(x),\cdots,y_m(x)]$ 的变分为

$\delta J=\frac{\partial J}{\partial y_1(x)}\delta y_1(x)+\frac{\partial J}{\partial y_2(x)}\delta y_2(x)+\cdots+\frac{\partial J}{\partial y_m(x)}\delta y_m(x)$ 。

变分法解决的三种问题：

拉格朗日问题

从容许函数类中求某一函数 $x(t)$ ，使得积分型泛函

$J=\int^{t_f}_{t_0}F(t,x(t),\dot{x}(t))dt$

取极小值问题。

迈耶尔（Mayer）问题

末值型泛函

$J=\Psi(x(t_f),t_f)$

取极小值问题。

波尔扎问题

复合型泛函

$J=\int^{t_f}_{t_0}F(t,x(t),\dot{x}(t))dt+\Psi(x(t_f),t_f)$

取极小值的变分问题。

定理2：如果函数 $F(t)$ 在区间 $\left[t_0,t_f \right ]$ 上连续，而且对于只满足某些一般条件的任意选定函数 $\eta(t)$ ，有

$\int^{t_f}_{t_0}F(t)\eta(t)dt=0$

则有

$F(t)=0\quad t\in\left[t_0,t_f \right ]$ 。

拉格朗日问题

考虑如下积分型的拉格朗日泛函极值问题：

$J=\int^{t_f}_{t_0}F(t,x(t),\dot{x}(t))dt$

其中， $x(t)$ 至少是 $t$ 的二次可微函数， $F(t,x(t),\dot{x}(t))$ 是变量 $t$ ， $x(t)$ 和 $\dot{x}(t)$ 的连续函数，并且有二阶连续偏导数。

假设1：曲线 $x(t)$ 的端点时间 $t_0$ 和 $t_f$ 是固定的，且满足如下边界条件

$x(t_0)=x_0,\quad x(t_f)=x_f$ ，

其中 $t_0$ ， $t_f$ ， $x(t)$ 和 $\dot{x}(t)$ 为泛函的宗量， $t$ 为积分变量。

利用泛函对其所有宗量进行一阶变分，为

$\begin{align*} \delta J&=\frac{\partial J}{\partial t_0}\delta t_0+\frac{\partial J}{\partial t_f}\delta t_f+\frac{\partial J}{\partial x(t)}\delta x(t)+\frac{\partial J}{\partial \dot{x(t)}}\delta \dot{x(t)}\\ &=F(t,x(t),\dot{x}(t))\delta t\left|^{t_0}_{t_f}\right.+\int^{t_f}_{t_0}(F_x\delta x(t)+F_{\dot{x}}\delta \dot{x}(t))dt \end{align*}$

其中 $F_x=\frac{\partial F(t,x(t),\dot{x}(t))}{\partial x(t)},\quad F_{\dot{x}}=\frac{\partial F(t,x(t),\dot{x}(t))}{\partial \dot{x}(t)}$ 。

由于 $\delta t_0=0,\delta t_f=0,\delta x(t_0)=0,\delta x(t_f)=0$ ，因此

$\delta J=\int^{t_f}_{t_0}[F_x-\frac{d}{dt}F_{\dot{x}}]\delta x(t)dt$ 。

根据定理2，可以得到极值条件

$F_x(t,x(t),\dot{x}(t))-\frac{d}{dt}F_{\dot{x}}(t,x(t),\dot{x}(t))=0$

将左边第二项展开，可得

$\begin{align*} & F_x(t,x(t),\dot{x}(t))-\frac{d}{dt}F_{\dot{x}}(t,x(t),\dot{x}(t))\\ =& F_x(t,x(t),\dot{x}(t))-\frac{\partial F(t,x(t),\dot{x}(t))}{\partial \dot{x}(t)\partial t}-\frac{\partial F(t,x(t),\dot{x}(t))}{\partial \dot{x}(t)\partial x(t)}-\frac{\partial F(t,x(t),\dot{x}(t))}{\partial \dot{x}(t)\partial \dot{x}(t)}\\ =&0 \end{align*}$

也可以简记为 $F_x-F_{\dot{x}t}-\dot{x}F_{\dot{x}x}-\ddot{x}F_{\dot{x}\dot{x}}=0$ 。

上式可以称为欧拉方程。欧拉方程的积分曲线 $x=x(t,C_1,C_2)$ 称为极值曲线。

只有在极值曲线上泛函 $J$ 才能达到极小（极大）值。
对于两个端点固定的情况，正好可以用两个边界条件 $x_0$ 和 $x_f$ ，将积分常数 $C_1$ 和 $C_2$ 固定起来。

假设2：假定容许函数的始端 $(t_0,x(t_0))$ 给定，末端 $(t_f,x(t_f))$ 可变，并假定沿着曲线 $c(t_f)$ 变化，寻找一条连续可微的极值曲线，使性能指标泛函

$J=\int^{t_f}_{t_0}F(t,x(t),\dot{x}(t))dt$

达到极值。

在该问题中， $t_0$ ， $t_f$ ， $x(t)$ 和 $\dot{x}(t)$ 为泛函的宗量， $t$ 为积分变量，为求得该泛函极值问题，引入拉格朗日乘子，并重新定义泛函为

$\tilde{J}=\lambda(t_f)\left(x(t_f)-c(t_f) \right )+\int^{t_f}_{t_0}F(t,x(t),\dot{x}(t))dt$

对其所有宗量进行一阶变分，为

$\begin{align*} \delta \tilde{J}&=\frac{\partial \tilde{J}}{\partial t_0}\delta t_0+\frac{\partial \tilde{J}}{\partial t_f}\delta t_f+\frac{\partial \tilde{J}}{\partial x(t)}\delta x(t)+\frac{\partial \tilde{J}}{\partial \dot{x}(t)}\delta \dot{x}(t)+\frac{\partial \tilde{J}}{\partial \lambda(t_f)}\delta \lambda(t_f)\\ &=\lambda(t_f)\delta x(t_f)+\lambda(t_f)\left(\dot{x}(t_f)-\dot{c}(t_f) \right )\delta t_f+F(t,x(t),\dot{x}(t))\delta t\left|^{t_f}_{t_0}\right.\\ &+\int^{t_f}_{t_0}(F_x\delta x(t)+F_{\dot{x}}\delta \dot{x}(t))dt+(x(t_f)-c(t_f))\delta \lambda(t_f) \end{align*}$

由于 $x(t_0)$ 固定，所以有 $\delta t_0=0$ 和 $\delta x(t_0)=0$ ，因此

$\begin{align*} \delta \tilde{J}&=\left[F+\lambda(t)\left(\dot{x}(t)-\dot{c}(t) \right ) \right ]\left|_{t_f}\right. \delta t_f+\left(\lambda(t)+F_{\dot{x}} \right )\left|_{t_f}\right.\delta x(t_f)\\ &+\int^{t_f}_{t_0}\left[F_x-\frac{d}{dt}F_{\dot x} \right ]\delta x(t)dt+(x(t_f)-c(t_f))\delta \lambda (t_f) \end{align*}$

其中 $\left[F+\lambda(t)\left(\dot{x}(t)-\dot{c}(t) \right ) \right ]\left|_{t_f}\right.=0$ 和 $\left(\lambda(t)+F_{\dot{x}} \right )\left|_{t_f}\right.=0$ 称为横截条件； $x(t_f)=c(t_f)$ 称为边界条件。

求解欧拉方程需要求解上述横截条件，由此可以求得欧拉方程中的通解中的积分常数和终端状态 $t_f$ 和 $x(t_f)$ 。

扩展：多个宗量函数的泛函极值问题

问题描述：寻找一条连续可微的极值曲线 $\mathbf x^*(t)$ 使得性能泛函

$J=\int^{t_f}_{t_0}F(t,\mathbf x(t),\dot{\mathbf x}(t))dt$

达到极值，该极值曲线的边界条件 $\mathbf x(t_0)=\mathbf x_0$ ， $\mathbf x(t_f)=\mathbf c(t_f)=\left[c_1(t_f), c_2(t_f), \cdots, c_n(t_f)\right ]^T$ 和 $\mathbf x(t)=\left[x_1(t), x_2(t),\cdots, x_n(t) \right ]^T$ 为 $n$ 维宗量向量函数。