目录
- 引言
- 线性空间的算子问题
- 变分的计算问题
- 欧拉公式
- 构造泛函的方法
- 利用分部积分构造
- 利用标准变分原理构造
- 瑞利一里茨法
- 加权留数法
- 本征问题
- 变分的实际应用
引言
- 由于课程后面重点的矩量法和有限元法都是基于变分法进行的,变分法是它们的数学基础,实际上矩量法就是电场积分方程变分法的实现,而有限元法则是电场微分方程的变分法实现。
- 变分法主要包括两大类,如下图所示:

- 直接法(Direct methods)
- 瑞利一里茨法(Rayleigh ritz)
- 间接法(indirect methods)
- 加权留数法
- 点匹配法(collocation)
- 子域法(subdomain)
- 伽辽金法(Galerkin)
- 最小二乘法(least square)
- 加权留数法
线性空间的算子问题
- 内积
- 定义内积:
对于两个点或者标量,其内积定义为:u和v的共轭相乘,然后在线性空间内进行积分
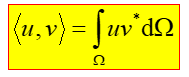
如果u和v是矢量的话,则上述内积公式写为:
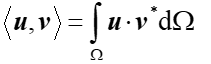
内积的运算法则:(第一个公式比较重要)
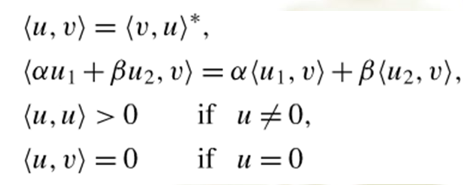
- 算子方程
定义算子方程
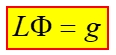
L是线性算子,Φ是未知函数,g是源函数
算子L所聚集的空间可以定义成内积的形式:
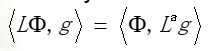
La是L的一个伴随算子,
若算子满足一定的条件的时候,具有一些特性:
(1)如果满足
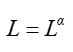
也就是说
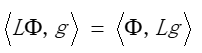
的时候,算子L是自伴的。
(2)如果对于算子L的域内任意的Φ不等于0的函数Φ有
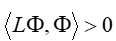
则称算子L是正定的;
(3)在(2)的基础上,反之如果
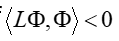
那么算子L是负定的 - example:证明以下拉普拉斯算子是自伴的:

变分的计算问题
- 泛函:泛函就是函数的函数,普通的实域空间的函数,函数自变量就是数,而泛函的自变量是函数。一个简单的例子,就是内积<u,v>,它就是一个泛函。
- 设定一个泛函如下:
欧拉公式
欧拉公式其实是泛函有极值的必要条件;
给定一个泛函如下:
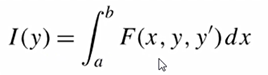
假定该泛函有极值,则该泛函的变分是等于零的,即:
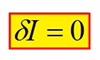
设h(x)是在y(x)上的一个很小的增量,那么y(x)+h(x)要满足边界条件:y(a) = A;y(b) = B
因为该泛函的变量是函数y,而函数y的自变量为x,而积分处的边界条件是从a到b积分,即a<x<b;
所以也可以知道,增量h(a) = h(b) = 0,因为此处函数都收束于一点,没有增量。
因此可以定义泛函的一个小的增量为:
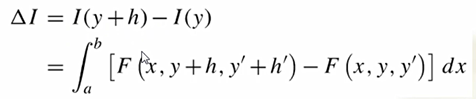
上述式子其实也可以定义为变分的离散化,变分就是泛函求微分,微分的离散化就是差分,而上述式子就是一种差分形式。
用泰勒级数对上述式子进行展开(分别在y+h和y+h` 进行展开)得到如下式子:
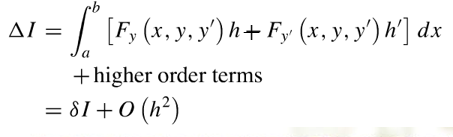
所以当两个差分点无限近,也就是h(x)无限小的时候,h和 h` 可以近似看成变分加上一个高阶无穷小量了。
因此,可以得到该泛函的近似变分为如下:
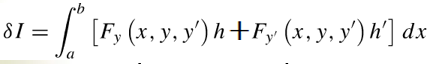
为了便于后面表示,用微分形式代替:
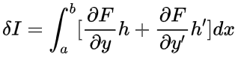
利用分部积分公式:
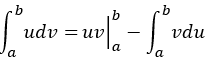
对变分公式中的第二项进行展开,即:
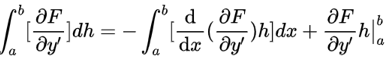
最后变分公式可以转化为如下形式:
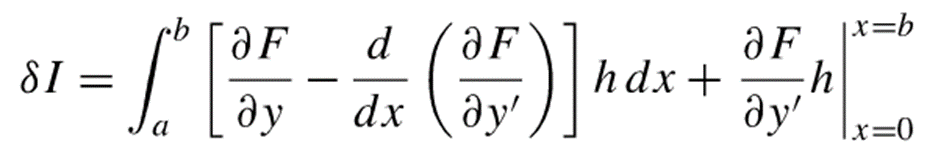
而之间我们已经讨论过h(x)在边界a、b处的值,所以后面这一项等于0,那么变分等于0可以表示成积分里这一项等于0:

其简写形式如下,这个就是叫做欧拉公式(或叫做欧拉-拉格朗日公式):
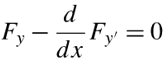
它的意义是:当泛函有极值的时候,该泛函的变分等于0,也就是存在该欧拉公式的形式。
更一般的情况,若泛函的变量的自变量为两个,即u = u(x,y),则有:
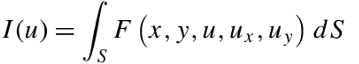
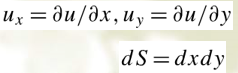
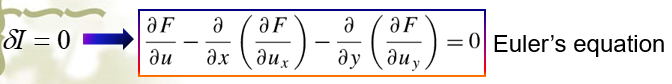
继续扩展,u = u(x,y);v = v(x,y)
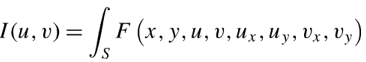
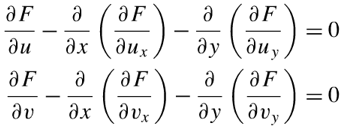
因此可以推断出通式,对于一个泛函:
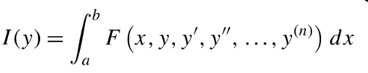
若该泛函存在极值,则欧拉公式为:
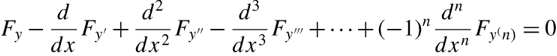
构造泛函的方法
利用分部积分构造
- 算子方程左乘一个变分δΦ,然后对整个域作积分;
- 使用散度定理或者分部积分的形式将被积式转换成变分δΦ;
- 利用边界条件;
- 将变分符号移动到积分号外就构造出一个泛函了;
举例:对于泊松方程如下:
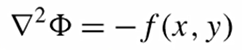
(1)将右边的f移到方程左边后,左乘一个变分,然后对整个域积分,得到新的方程:δI = 0,而δI就是下面式子的积分,所以可以知道,如果把积分里的δ(变分符号)提到积分外,则该积分就是一个泛函了,也就是实现了由算子方程构造出了要给泛函。(积分里面多了负号,实际上没有什么影响,因为方程右边是0,只是为了后面简化过程比较直观所以多乘了一个负号)
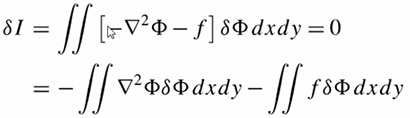
(2)然后再利用分部积分法,先把δΦ看成一个整体,Φ对x的偏微分看成一个整体,然后就有:
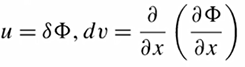
同理就有:
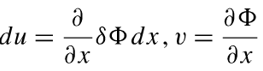
回顾一下分部积分公式:
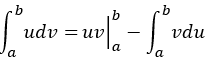
对最初的积分式子左边的项进行分部积分展开:
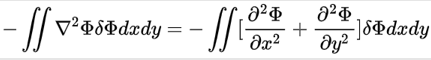
对Φ的x二阶偏微分和y的二阶偏微分都进行分部积分展开:
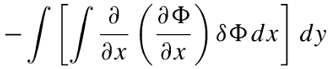
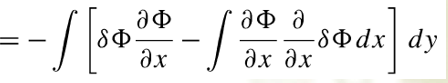
最后可以得到:
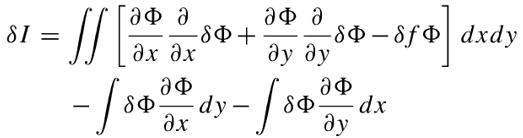
(3)为了把变分符号移到积分符号外,利用了变分的性质:
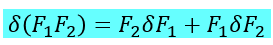
最后得到如下式子:
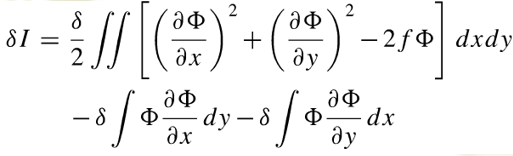
(4)后面两项,利用边界条件(对于齐次的边界条件,要么是Φ=0,要么是Φ的导数等于0,即Dirichlet边界条件或Neumann边界),所以后面这两项都等于0了;
再将1/2移到积分内,得到最终的变分公式:
(关于边界条件的知识可以参考偏微分方程的三类边界条件以及求解微分方程的边界条件)
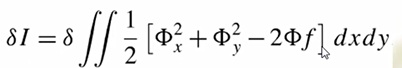
最后再将变分符号去掉,便得到了泛函函数I:
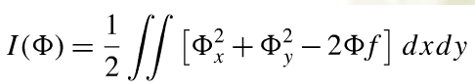
利用标准变分原理构造
瑞利一里茨法
瑞利一里茨实际上就是用了标准变分法原理来构造;
对于泛函I:
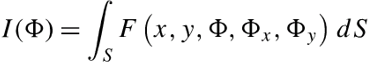
利用多项式级数来近似Φ函数,其中un定义为展开函数(或叫做基函数),