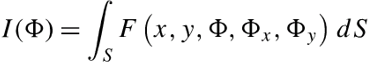是《最优控制理论与应用(邵克勇，王婷婷，宋金波)》的读书笔记，相比于其他的书，选择这本书的理由是页数少，能读完。解学书的《最优控制理论与应用》看目录感觉很全，但是太厚了，感觉看不完。

虽然用过h2和h无穷的方法，但是对原理不是了解的很透彻，就是会用。

本章的逻辑线大概是：什么是泛函？（函数的对应值）——>变量的变分——>微小变化——>连续（k阶连续）——>线性泛函——>泛函的变分——>泛函的极值——>泛函的极值定理

 

 

---

2.1 泛函与变分

• 泛函
  • 定义
    • 泛函可简单理解为“函数的函数”
    • 对应于定义域中的每一个值x,y都有一个（或一组）值与之对应，则称y是x的函数，记为y=f（x）。这里x是自变量，y是因变量。
    • 对应于某一类函数中的每一个确定的函数y（x）（注意，不是函数值），因变量J都有一个确定的值（注意，不是函数）与之对应，则称因变量J为函数y（x）的泛函数，简称泛函。记为J=J【y（x）】或简单记为J。也就是说，泛函可简单理解为“函数的函数”，
    • 它经常以定积分的形式出现。
  • 例子
    • 1

      

    • 可见，x（t）表示一类函数，一旦函数的表达式确定，则J的值是确定的.J的值随函数x（t）的确定而确定，是一个泛函。
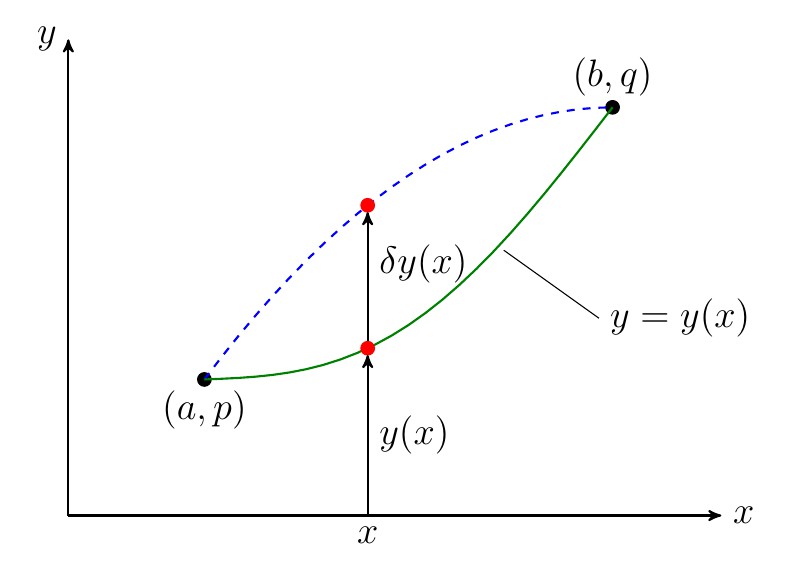
  • （2）泛函的变量y（x）的变分
    • 泛函J【y（x）】的变量y（x）的增量

      

    • 也称变量y（x）的变分，记为

      

    • 其中y（x）假定是在某一类函数中任意改变的，有时简记8y（x）为8y。
  • （3）泛函的连续性
    • 若对于变量y（x）的微小改变，存在与之对应的泛函J【y（x）】的微小改变，则称泛函J【y（x）】为连续的。
    • 其中，变量y（x）的微小改变的含义是，对于y（x）与y0（x）有定义的所有x值，|y（x）-y0（x）|很小，表示成下式

      

    • 其中ε是一个任意给定的很小的正数，则称y（x）与y0（x）有零阶接近度。如图2-2所示，但是它们具有零阶接近度
      • 1

        

    • 一阶接近度
      • 如果不仅|y（x）-y0（x）|很小，而且|y（x）-y0（x）|也很小，这也意味着y（x）与y0（x）有微小改变，称这种微小改变具有一阶接近度，如图2-3所示。

        

    • k阶接近度

      

    • k阶连续

      

  • （4）线性泛函

    

  • （5）泛函的变分（或增量）*
    • 当宗量函数y（x）有变分δy（x）时，连续泛函J【y（x）】的增量可以表示为

      

    • 式中
      • 宗量y(x)的变分

        

      • 泛函的变分

        

        • 泛函增量的线性主部，它是δy（x）的线性连续泛函
        • 由此可知，泛函的变分是泛函增量的线性主部，所以泛函的变分也可以称为泛函的微分。
        • 当泛函的变分存在，即其增量△J可用式（2-7）表达时，则称泛函是可微的
      • 高阶无穷小量
        • 1

          

      • 例子
        • 1

          

        • 常用定理
          • 1

            

            

            

          • 例子

            

    • 变分规则
      • 1

        

  • （6）泛函的极值
    • 极小值
      • 在y0(x)处

        

    • 极大值
      • 在y0(x)处

        

    • 强极值
      • 泛函极值是一个相对的比较概念，如果y（x）与y0（x）具有零阶接近度，则泛函达到的极值为强极值；
    • 弱极值
      • 如果y（x）与y0（x）具有一阶（或一阶以上）接近度，则泛函的极值为弱极值
    • *
      • 显然，在y（x）上达到强极值的泛函，必然在y0（x）上达到弱极值，但反之不一定成立。
      • 同时，强极值是范围更大的一类曲线（函数）的泛函中比较出来的，所以强极大值大于或等于弱极大值，而强极小值小于或等于弱极小值
    • 泛函极值定理
      • 1

        

      •