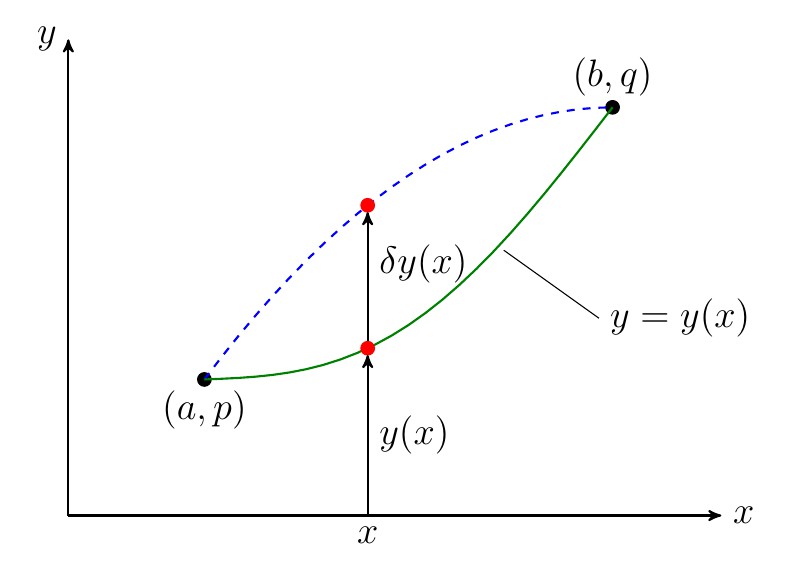
1696年约翰·伯努利在写给他哥哥雅克布·伯努利的一封公开信中提出了如下的“捷线”问题：设想一个质点沿连接点A和一个更低的点B的一条曲线无摩擦力地下滑，如果质点仅在重力的影响下，那么沿怎样一条曲线才使质点下滑所需时间最少？
容易看出，质点沿不同路径降落所需时间是不一样的，直线决不是最快的路径，答案也不是圆弧或其他初等曲线。

我们认识到，在微分法处理极小问题时，要求极小的量仅依赖于一个或若干个数值变量，而捷线问题中考虑的下降时间，却依赖整条曲线。这是一个本质上的不同，因此这个问题不能由微分法来解决。

变分法 费马光学原理

伯努利兄弟和其他人已经找到了解捷线问题的各种不同方法，最初这些方法是对特殊问题而采用的，没过多久，欧拉和拉格朗日(Lagrange,1736-1813)发展出解这种极值问题(自变元不是有限个数值变量而是整个曲线或函数的极值问题)的更一般的方法，叫做变分法。

这里不介绍这些方法的技术细节。变分法在物理中应用很广，很早以前人们就注意到，自然现象常常呈现为某种类型的极大或极小形式。例如赫伦的光线定理：光线由P经平面镜反射到Q所走的路径是P到反射点L再到Q的所有可能路径中的最短路径。这是对平面镜反射定律的另一种阐述。在17世纪，费马对此更进了一步，他观察到，光线的折射定律也可以借助极小定理来描述。

图1 光线的折射定律

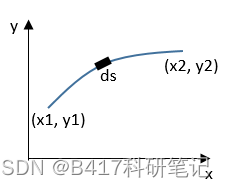
我们知道，光线由一均匀介质传播到另一均匀介质时，路径将发生偏折，如上图在I介质中光线速度为v，在II介质中速度为w，则光由P到R的传播路径PQ,QR，由条件

$$\frac{sin\alpha }{sin{\alpha }^{\prime }}=\frac{v}{w}$$

给出。利用微积分，费马证明了这路径使光线由P到R所需的时间最少。这是对光线折射定律的重新阐述，但是这样的一个极小原理的阐述不仅仅只是折射定律换个说法，它比原先的折射定律涵义更为深刻。费马将这个定律推广到其他情形，直到一种任意的光学系统：在这个系统中，光线的速度按一定的方式逐点变化。费马把连续的非均匀介质分割成许多薄层，在每一层光速近似不变，通过从一个薄层到下一个薄层逐次应用他的原理，再将薄层厚度趋于零，费马得到了普遍的几何光学的费马原理：在非均匀介质中，光线在两点间传播要沿着连接该两点的一切路径中费时最少的一条路径前进。

极小原理在物理学的其他分支中也起着支配的作用。比如力学系统的最小作用量原理，它是由哈密尔顿(W.R. Hamilton,1805-1865)从欧拉变分原理推广而来，是力学、光学、电动力学的基础之一，并且在工程中有许多应用。同样，费曼对量子力学的路径积分阐述也是由最小作用量原理向微观系统的推广得来。于是，我们可以看到变分法对现代科学的卓越贡献。

最速下降线问题

回到最速下降线问题上来，我们不讨论解的存在性问题，仅对雅克布·伯努利得到的捷线问题的解法进行一个介绍。这个解法不需很多专业知识就能理解。
首先我们认识到一个力学中的事实：一个质点由A点沿任意曲线静止下滑，到达P点时的速度与A到P的垂直距离h的1/2次方成比例。即由于$mgh=\frac{1}{2}m{v}^2$可以得出$v=c\sqrt{h}$，这里c是常数。
接下来将A到P的空间分成n个薄片，如下图，每一片厚度为d，并假定质点在每一薄片上速度是一样的，那么从A开始到第一个薄片速度为$v=c\sqrt{d}$，第二片

图2

为$v=c\sqrt{2d}$，依次递增，第n片为$v=c\sqrt{nd}=c\sqrt{h}$