我的前一篇文章介绍了对于分配问题的Kuhn-Munkre算法，该算法其实可以看作是邻接矩阵形式的匈牙利算法，如果更抽象地看这个算法，它可以看成是一个二分图匹配算法的变体算法，具体的说，是二分图最大权重匹配算法。我打算也把二分图最大权重匹配算法也介绍下，不过最大权重匹配算法又是基于最大匹配算法设计的，所以这篇文章先介绍二分图的最大匹配算法

二分图最大匹配问题

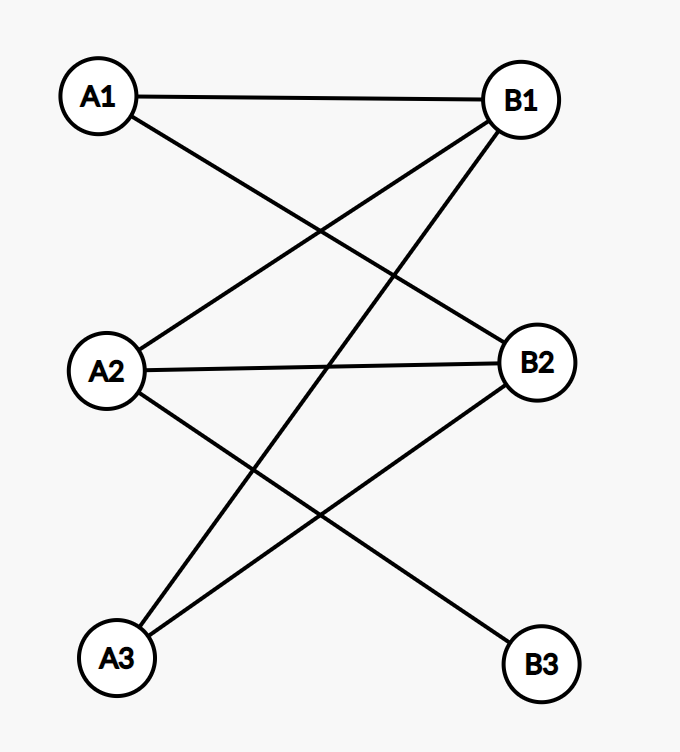
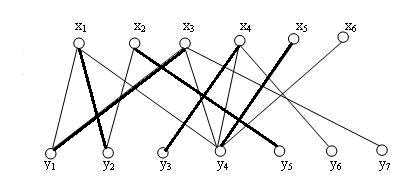
分配问题从图论的角度看其实是一个二分图(Bipartite Graph)，就是说图中有两个点集，在各自的点集内的点互相没有连接，两个点集间的点可以连接，每个点存在多个允许的连接，如下图所示：

如果我们对二分图中的每个点，都确定最多只有一条连接，那么称之为该二分图的一个匹配，例如：

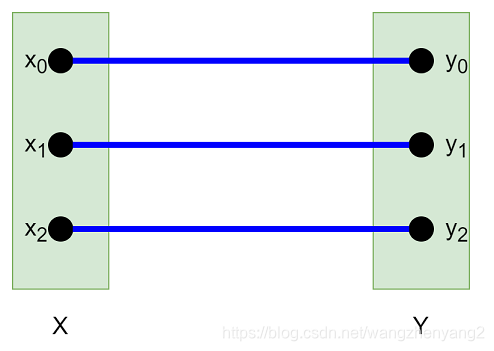
如果每个点都有一条线确定，即匹配的线数正好等于单个点集点数$n$，那么称之为完美匹配，如下图：

对应于现实问题，我们当然希望尽量达到完美匹配，但是因为点的可选连线情况可能导致无论如何也达不到完美匹配，所以自然而然产生了最大匹配问题(Max-Bipartite Matching)，最大可以找到多少条匹配线

用数学语言描述：

• 图$G=(V,E)$是一个二分图，$n=|V|$，$m=|E|$，$\delta (v),v\in V$表示一端连接到点$v$的所有边， x e ∈ { 0 , 1 } x_e\in \{0,1\} xe​∈{0,1}表示边$e$是否被选中，则有最大匹配问题：
  m a x ∑ e ∈ E x e s . t . ∑ e ∈ δ ( v ) ≤ 1 , ∀ v ∈ V x e ∈ { 0 , 1 } , ∀ e ∈ E \begin{aligned} max\quad& \sum_{e\in E} x_e\\ s.t.\quad& \sum_{e\in \delta(v)}\leq 1,\forall v \in V \\ & x_e\in \{0,1\},\forall e \in E \\ \end{aligned} maxs.t.​e∈E∑​xe​e∈δ(v)∑​≤1,∀v∈Vxe​∈{0,1},∀e∈E​

算法主流程

在介绍算法前，先定义一些专用的算法术语，这些术语是算法的必备要素

• 自由顶点(free vertex)：就是指当前匹配结果下没有任何连线的点
• 交替路径(alternating path): 由匹配边和非匹配边交替构成的一条路径，例如下面的图，加重的边表示已经在当前匹配中确定的边，细线表示还没确定的边
  
• 增广路径(augmenting path)：属于交替路径，不过它的首末顶点都是自由顶点，即开头和最后的两条边必须是非匹配边，如下图所示
  

我们观察一下增广路径，它是一条匹配边接一条非匹配的构造，并且首末两条边都是未确定的，如果我们把这个路径"翻转"一下，把匹配边变成非匹配，非匹配变为匹配，那么可以发现，这条路径上的匹配数会多出1：

这就给了我们启发，只要我们能在当前匹配的二分图中找到一条增广路径，那么就能扩充1数量的匹配；从数学理论上看也确实如此，最大匹配算法的理论前提就是：

• 对于一个二分图，一个匹配$M$是最大的，当且仅当图$G$在$M$的基础上找不到任何增广路径

自然地，我们就得到了算法的主流程：

1. 初始化匹配$M$，$M=\varnothing$
2. 在当前匹配的基础上，在图$G$中搜索增广路径$P$
3. 如果存在$P$，对增广路径进行翻转更新匹配$M$，回到步骤2
4. 输出$M$

搜索增广路径

但是怎么搜索增广路径还是需要一个专门的子算法来处理；搜索过程一定是从一个自由顶点开始，到一个自由顶点结束，并且匹配边与非匹配边交替进行；这里介绍一种把匹配图转化成有向图的深度优先路径搜索算法：新增一个首节点$s$和一个末结点$t$，对于当前二分图中未确定的边，我们将其方向置为$X$到$Y$，对于匹配边，将方向置为$Y$到$X$；对于$X$中未匹配的点，我们添加从$s$到该点的边；对于$Y$中未匹配的点，我们添加从该点到$t$的边；这样二分图变成了一个有向图，我们采用深度优先遍历搜索从$s$到$t$的最短路径，如果能搜索到一条路径，那么去掉首末结点后就是一条增广路径

举个例子，当前二分图的匹配如下图所示：

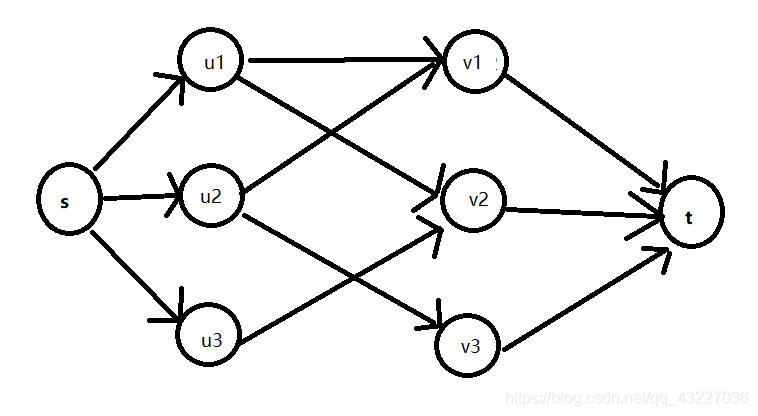
将其转化成一个有向图：

然后我们就可以搜索到一条最短路径$s\to x_0\to y_0\to x_1\to y_1\to t$，去掉$s$和$t$，就是一条增广路径

代码实现

我写了一段python代码来实现上述的算法过程。定义了MaxMatchAlgorithm类，它只需要一个边矩阵作为输入，矩阵的行列分别表示二分图的$X$和$Y$，矩阵的每个元素表示该边是否可选；maxMatch实现了算法的主流程，getAugmentingPath方法用于搜索增广路径，invert方法则用于翻转增广路径

import numpy as npclass MaxMatchAlgorithm:def __init__(self, edges):'''edges : Matrix with num_x X num_y size'''self.num_x=edges.shape[0]self.num_y=edges.shape[1]self.edges=edgesdef maxMatch(self):matches=[]iter=1while True:print("######## iteration "+str(iter)+" ##############")print("...")print("...")iter+=1augPath=self.getAugmentingPath(matches)if len(augPath)==0:breakmatches=self.invert(augPath,matches) return matchesdef invert(self, augPath, matches):for i in range(len(augPath)):if i%2==0:if augPath[i][2]:matches.append((augPath[i][0],augPath[i][1]))else:matches.append((augPath[i][1],augPath[i][0]))else:removeIndex=-1for index in range(len(matches)):if (matches[index][0]==augPath[i][0] and matches[index][1]==augPath[i][1]) or (matches[index][0]==augPath[i][1] and matches[index][1]==augPath[i][0]):removeIndex=indexbreakmatches.pop(removeIndex)return matchesdef getAugmentingPath(self,matches):#directMatrix[i,j]=1 : x_i -> y_jtotalVertexN=self.num_x+self.num_y+2directMatrix=np.zeros((totalVertexN,totalVertexN))for i in range(0,totalVertexN-1):for j in range(0,totalVertexN):if i==0 and j>=1 and j<=self.num_x:directMatrix[i,j]=1continueif j==totalVertexN-1 and i>self.num_x:directMatrix[i,j]=1continueif i==j or i==0 or j==0 or j==totalVertexN-1:continueiIsX=FalsejIsX=Falseif i>0 and i<=self.num_x:iIsX=Trueelif i>self.num_x and i<=totalVertexN-2:iIsX=Falseif j>0 and j<=self.num_x:jIsX=Trueelif j>self.num_x and j<=totalVertexN-2:jIsX=Falseif iIsX and jIsX==False:directMatrix[i,j]=self.edges[i-1,j-1-self.num_x]for (x,y) in matches:directMatrix[x+1,y+1+self.num_x]=0directMatrix[y+1+self.num_x,x+1]=1for j in range(1, self.num_x+1):isMatched=Falsefor k in range(self.num_x, totalVertexN-1):if directMatrix[k][j]==1:isMatched=Truebreakif isMatched:directMatrix[0][j]=0for i in range(self.num_x, totalVertexN-1):isMatched=Falsefor k in range(1, self.num_x+1):if directMatrix[i][k]==1:isMatched=Truebreakif isMatched:directMatrix[i][totalVertexN-1]=0shortestRoute=self.findRoute(directMatrix,[0],[])augmentingPath=[]for i in range(1,len(shortestRoute)-2):vertexIndex_A=shortestRoute[i]actualIndex_A=0vertexIsX_A=Falseif vertexIndex_A>=1 and vertexIndex_A<=self.num_x:actualIndex_A=vertexIndex_A-1vertexIsX_A=Trueelse:actualIndex_A=vertexIndex_A-1-self.num_xvertexIndex_B=shortestRoute[i+1]actualIndex_B=0vertexIsX_B=Falseif vertexIndex_B>=1 and vertexIndex_B<=self.num_x:actualIndex_B=vertexIndex_B-1vertexIsX_B=Trueelse:actualIndex_B=vertexIndex_B-1-self.num_xaugmentingPath.append((actualIndex_A,actualIndex_B,vertexIsX_A))return augmentingPathdef findRoute(self, directMatrix, currentRoute, currentShortestRoute):if currentRoute[-1]==directMatrix.shape[0]-1:if len(currentShortestRoute)==0 or len(currentShortestRoute)>len(currentRoute):currentShortestRoute=currentRoute.copy()return currentShortestRoutefor i in range(0,directMatrix.shape[0]):if directMatrix[currentRoute[-1],i]==1:nextRoute=currentRoute.copy()nextRoute.append(i)route=self.findRoute(directMatrix, nextRoute,currentShortestRoute)if len(currentShortestRoute)==0 or len(currentShortestRoute)>len(route):currentShortestRoute=route.copy()return currentShortestRoute

用下面的代码测试，输入数据就是上面的例子：

import numpy as np
from MaxMatchAlgorithm import MaxMatchAlgorithm  edges=np.array([[1,0,1],[1,1,1],[0,0,1]
])maxMatchAlgorithm=MaxMatchAlgorithm(edges)
print(maxMatchAlgorithm.maxMatch())

结果

对应图上就是