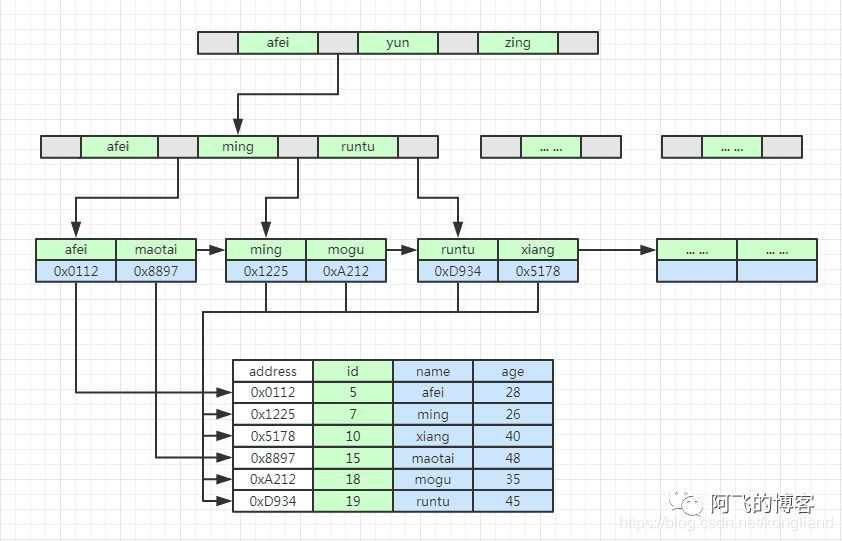
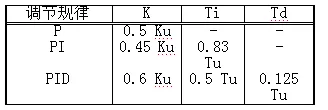
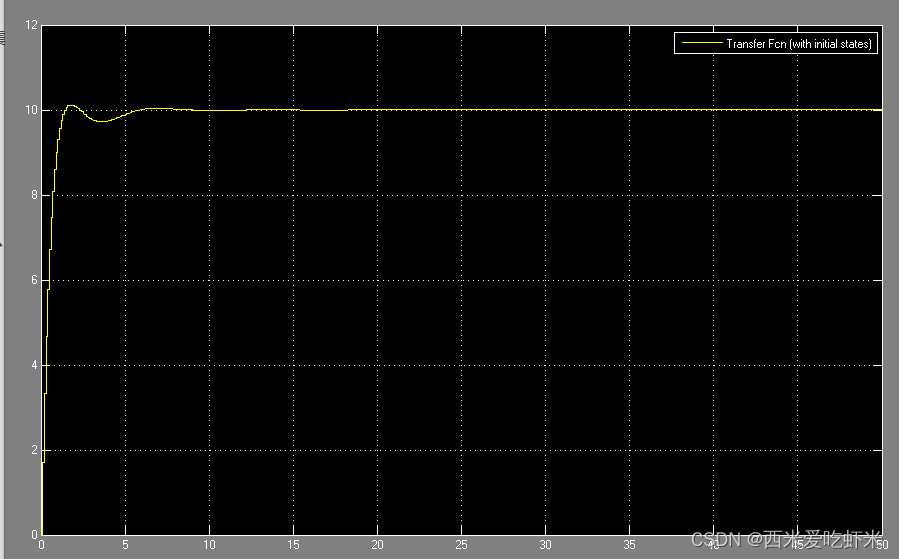
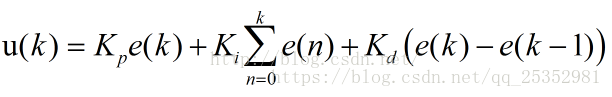递归法思路:
树的高度即节点子树的高度+1(节点子树的高度即左子树高度,右子树高度的最大值)
代码如下:
// Height_Recursive 递归法求树的高度
int Height_Recursive(TreeNode* pTree) {if (pTree == NULL) {return 0;}// 分别求出左子树,右子树的高度,取最大值+1int leftHeight = Height_Recursive(pTree->left);int rightHeight = Height_Recursive(pTree->right);return (leftHeight > rightHeight ? leftHeight: rightHeight)+1;
}非递归法思路:
借鉴程序遍历的思想,一层层的遍历,累加层数即可得到树的高度
代码如下:
// Height_No_Recursive 非递归法求树的高度
// 思路:借鉴层序遍历的思想,一层层的遍历,层数即高度
int Height_No_Recursive(TreeNode* pTree) {if (pTree == NULL) {return 0;}queue<TreeNode*> que;que.push(pTree);int height = 0;TreeNode* p = NULL;while(!que.empty()){height++;// 该层的节点个数,压入所有节点的孩子节点int num = que.size();for (int i=0;i<num;i++){p = que.front();que.pop();if (p->left != NULL){que.push(p->left);}if (p->right != NULL){que.push(p->right);}}}return height;
}实验结果如下图:
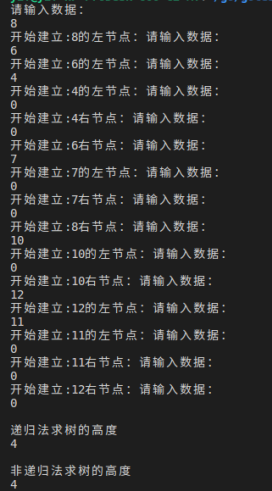
完整代码如下:
#include<iostream>
#include<queue>
using namespace std;// 树(节点)定义
struct TreeNode
{int data; // 值TreeNode* left; // 左节点TreeNode* right;// 右节点
};// 按照前序建立二叉树,这里我们建立下面的树
// 8
// 6 10
// 4 7 12
// 11
// 所以输入顺序是:8 6 4 0 0 7 0 0 10 0 12 11 0 0 0
void createTree(TreeNode*& t)
{ cout<<"请输入数据:"<<endl;int val = 0;cin>>val;// 0表结束if (0 == val){t = NULL;}else {t = new TreeNode();t->data = val;cout<<"开始建立:"<<val<<"的左节点:";createTree(t->left);cout<<"开始建立:"<<val<<"右节点:";createTree(t->right);}
}// Height_Recursive 递归法求树的高度
int Height_Recursive(TreeNode* pTree) {if (pTree == NULL) {return 0;}// 分别求出左子树,右子树的高度,取最大值+1int leftHeight = Height_Recursive(pTree->left);int rightHeight = Height_Recursive(pTree->right);return (leftHeight > rightHeight ? leftHeight: rightHeight)+1;
}// Height_No_Recursive 非递归法求树的高度
// 思路:借鉴层序遍历的思想,一层层的遍历,层数即高度
int Height_No_Recursive(TreeNode* pTree) {if (pTree == NULL) {return 0;}queue<TreeNode*> que;que.push(pTree);int height = 0;TreeNode* p = NULL;while(!que.empty()){height++;// 该层的节点个数,压入所有节点的孩子节点int num = que.size();for (int i=0;i<num;i++){p = que.front();que.pop();if (p->left != NULL){que.push(p->left);}if (p->right != NULL){que.push(p->right);}}}return height;
}int main()
{TreeNode* pTree = NULL;createTree(pTree);cout<<"\n递归法求树的高度"<<endl;cout<<Height_Recursive(pTree)<<endl;cout<<"\n非递归法求树的高度"<<endl;cout<<Height_No_Recursive(pTree)<<endl;return 0;
}