二分图最大匹配
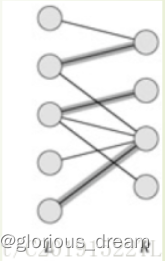
二分图最大匹配问题: 有两个集合A,B,两个集合间有多条边连接集合中的点,且单个集合中的点各不相连,求两集合的点能两两配对的最大匹配数.
(参考:)二分图最大匹配——匈牙利算法
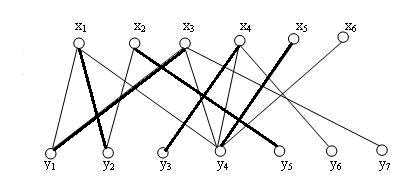
匈牙利算法: A集合记录各点与B集合相连的点,B集合记录某点与A集合中匹配的点.遍历A集合中的每一点,寻找最大匹配.
每一点顺序选取B集合中没被匹配过的点,若有,则将B集合中的点与该点匹配,跳转至下一个点.
若没有未匹配的点,顺序遍历所有有连接的点,看该点已匹配的点能否选择其他点去匹配,这是一个递归过程.
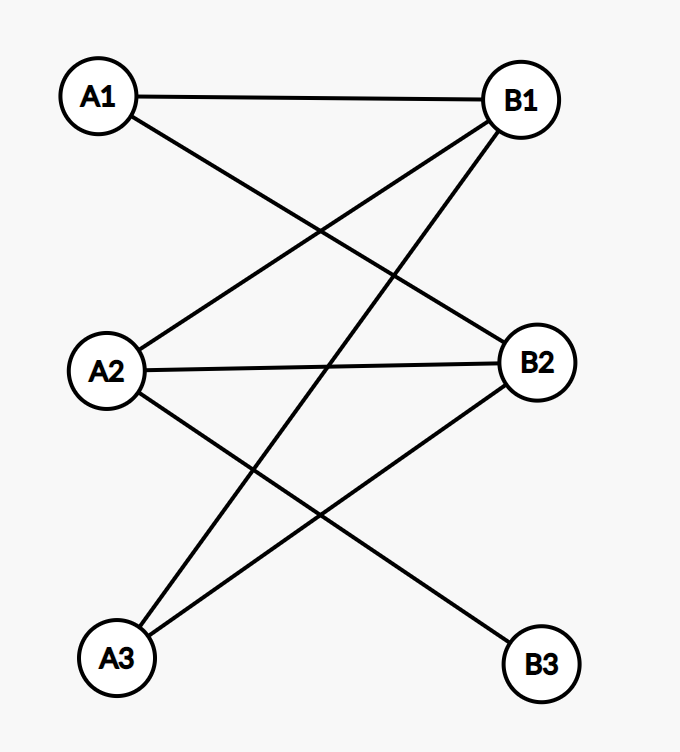
如:A1与B1,B2连;A2与B1,B2,B3连;A3与B1,B2连.在处理A3前,A1-B1,A2-B2相匹配,处理A3时,发现所有与A3相连的点都有匹配对象了.这时递归到B1匹配点A1,发现A1其他的点也均被匹配;再递归除B1外的第一个B2,发现B2的匹配点A2可以匹配B3,所以可以增加最大匹配数.
此时,令A2-B3,递归返回,A1-B2,递归返回,A3-B1.
时间复杂度:O(nm)(也称O(VE))
例题:P3386 【模板】二分图最大匹配
#include<bits/stdc++.h>
#define MAXN 505
using namespace std;struct Hungary
{struct NODE{int f,vis;set<int>to;};NODE node[MAXN];void add(int u,int v){node[u].to.insert(v);}int dfs(int x){if(node[x].vis)return 0;node[x].vis=1;for(auto& j:node[x].to){if(!node[j].f||dfs(node[j].f)){node[j].f=x;return 1;}}return 0;}int hungary(int n){int tot=0;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){node[j].vis=0;}tot+=dfs(i);}return tot;}
};int n,m,e,u,v;
Hungary a;
int main()
{cin>>n>>m>>e;for(int i=1;i<=e;i++){cin>>u>>v;a.add(u,v);}int tot=a.hungary(n);cout<<tot;return 0;
}
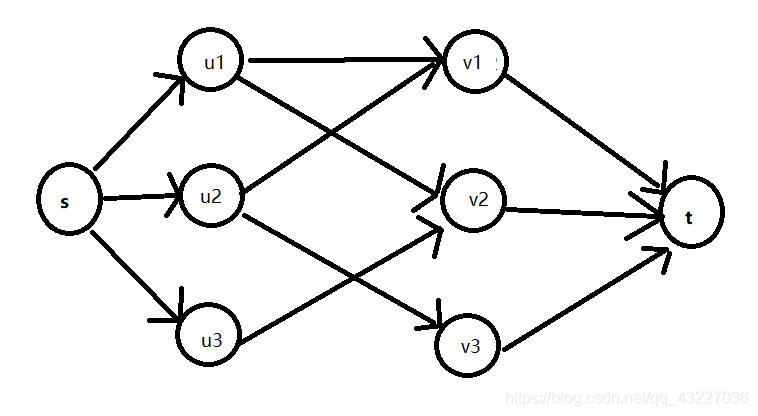
Dinic网络流算法:
需要了解网络流
设立超级源点s和超级汇点t,作s到A集合所有点的有向边,B集合所有点到t的有向边,A,B集合的边按题目连接,所有边的最大容量设置为1。最终流向t的最大流即为二分图最大匹配。
这个算法比匈牙利稍快,时间复杂度O(sqrt(n) * m),但空间消耗较大
//ErFenTuZuiDaPiPei_dinic
#include<bits/stdc++.h>
#define ll long long
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define DEBUG cout<<",here\n";
#define MAXN 1205
using namespace std;struct EDGE
{ll c;//capacityll flow;EDGE():c(0),flow(0){}
};EDGE a[MAXN][MAXN];
vector<ll>link[MAXN];
ll ceng[MAXN];ll n,m,s,t,u,v,c,e,maxn,ans=0;ll bfs()//构建层级网络,一次bfs就行了,很简单
{memset(ceng,0,sizeof(ceng));queue<ll>q;q.push(s);ceng[s]=1;while(!q.empty()){ll now=q.front();q.pop();for(auto& i:link[now]){if(ceng[i]==0 && a[now][i].c-a[now][i].flow>0){ceng[i]=ceng[now]+1;q.push(i);}}}if(ceng[t])return 1;//能构建,继续之后的dfsreturn 0;//不能构建更多了,没有更多的增广路了
}//有当前弧优化
ll dfs(ll now,ll minflow)
{if(now==t){ans+=minflow;return minflow;}ll ret=0,minflow2;for(auto& i:link[now]){if(ceng[i]==ceng[now]+1 && a[now][i].c-a[now][i].flow>0){minflow2=dfs(i,min(minflow,a[now][i].c-a[now][i].flow));if(minflow2==0)ceng[i]=0;//debuga[now][i].flow+=minflow2;a[i][now].flow-=minflow2;minflow-=minflow2;//剩余容量减少,以便从该节点直接再往后找增广路,//提高效率,当前弧优化ret+=minflow2;//dfs找到的最小剩余容量之和if(minflow==0)break;}}return ret;//返回从这个节点开始之后找到的所有增广路的流量之和
}int main()
{maxn=pow(2,31);scanf("%lld%lld%lld",&n,&m,&e);for(ll i=1;i<=e;i++){scanf("%lld%lld",&u,&v);v+=n;a[u][v].c+=1;link[u].push_back(v);link[v].push_back(u);}s=0,t=n+m+1;for(ll i=1;i<=n;i++){a[s][i].c+=1;link[s].push_back(i);link[i].push_back(s);}for(ll i=n+1;i<=n+m;i++){a[i][t].c+=1;link[i].push_back(t);link[t].push_back(i);}while(bfs()){dfs(s,maxn);}printf("%lld",ans);return 0;
}