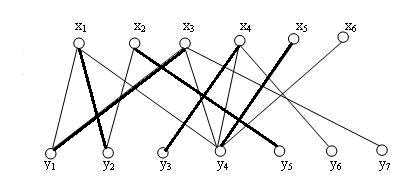
二分图最大匹配

（一）、二分图

1、定义

二分图又称作二部图，是图论中的一种特殊模型。
设G=(V, E)是一个无向图。如果顶点集 V可分割为两个互不相交的子集X和Y，并且图中每条边连接的两个顶点一个在 X中，另一个在 Y中，则称图G为二分图。

2、性质

定理：当且仅当无向图G的每一个环
的结点数均是偶数时，图G才是一个二分图。如果无环，相当于每的结点数为 0，故也视为二分图。

3、判定

如果一个图是连通的，可以用如下的染色法判定是否二分图：
我们把X部的结点颜色设为0，Y部的颜色设为1。
从某个未染色的结点u开始，做BFS或者DFS 。把u染为0，枚举u的儿子v。如果v未染色，就染为与u相反的颜色，如果已染色，则判断u与v的颜色是否相同，相同则不是二分图。
如果一个图不连通，则在每个连通块中作判定。

代码如下：

#include<cstdio>
#include<queue>
using namespace std;
#define MAX_N 100
bool flag=true;//记录答案
bool G[MAX_N