算法：

这一类题目很简单，不过却是树的最基本操作之一，引申为判断树是不是平衡二叉树。

一般做法是，计算二叉树的左右子树的高度+1，然后取它们的最大值或者最小值。

题目1:

https://leetcode-cn.com/problems/balanced-binary-tree/

代码实现：

/*** Definition for a binary tree node.* type TreeNode struct {*     Val int*     Left *TreeNode*     Right *TreeNode* }*/// 一棵平衡二叉树，左右两棵子树的高度差的绝对值不超过1// 备注：其中任意一个节点如果不满足平衡二叉树时，那么这棵树就不是平衡二叉树了，此时我们可以直接返回flase
func isBalanced(root *TreeNode) bool {if root == nil { // nil表示的是平衡二叉树return true}// 1.用来计算当前节点的左右子树高度差是1lH := maxDepth(root.Left)rH := maxDepth(root.Right)if abs(lH-rH) > 1{return false}// 2. 进一步判断左子树是不是平衡二叉树if !isBalanced(root.Left) {return false}// 3. 进一步判断右子树是不是平衡二叉树return isBalanced(root.Right)
}
// 典型的计算二叉树的高度，当前左右子树的最大高度+1
func maxDepth(root *TreeNode) int {if root == nil { return 0}return max(maxDepth(root.Left),maxDepth(root.Right)) + 1
}func max(a,b int) int {if a > b {return a}return b
}
func abs(a int) int {if a < 0 {return -a}return a
}

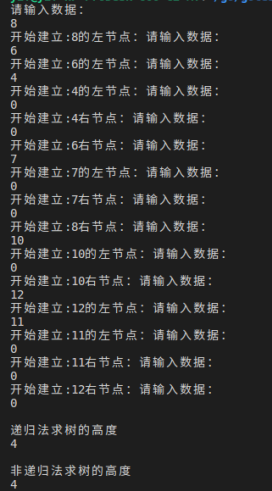
执行结果：

题目2:
https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/

代码实现：

/*** Definition for a binary tree node.* type TreeNode struct {*     Val int*     Left *TreeNode*     Right *TreeNode* }*/
func maxDepth(root *TreeNode) int {if root == nil {return 0}left := maxDepth(root.Left)right := maxDepth(root.Right)if left > right {return left + 1}return right + 1
}
/*
递归算法：
左右子树的高度最大数值+1
*/

执行结果：

题目3:

https://leetcode-cn.com/problems/minimum-depth-of-binary-tree/

代码实现：

/*** Definition for a binary tree node.* type TreeNode struct {*     Val int*     Left *TreeNode*     Right *TreeNode* }*/
func minDepth(root *TreeNode) int {if root == nil {return 0}if root.Left ==nil && root.Right == nil {return 1}min := int(^uint(0) >> 1)if root.Left != nil { // 对于一个孩子的节点，要计算有孩子节点的高度h := minDepth(root.Left)if min > h {min = h}}if root.Right != nil {h := minDepth(root.Right)if min > h {min = h}}return min+1
}

执行结果：

题目4:

https://leetcode-cn.com/problems/maximum-depth-of-n-ary-tree/

代码实现：

/*** Definition for a Node.* type Node struct {*     Val int*     Children []*Node* }*/func maxDepth(root *Node) int {if root == nil {return 0}var hs []intfor _, n := range root.Children {h := maxDepth(n)hs = append(hs,h)}max := 0for _,h:=range hs {if h > max {max = h}}return max + 1
}

执行结果：