二分图最大匹配与最大独立集

article/2025/9/17 10:05:40

一.概念部分

1.什么是二分图？

通俗的说法：就是可以把图分成两部分，每一部分任意两点之间没有关系（同一部落），两部分之间点可能存在多种关系。

2.怎么判断二分图？

（1）理论判定：如果某个图为二分图，那么它至少有两个顶点，且其所有回路的长度均为偶数，任何无回路的的图均是二分图。

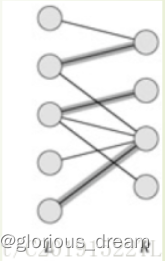
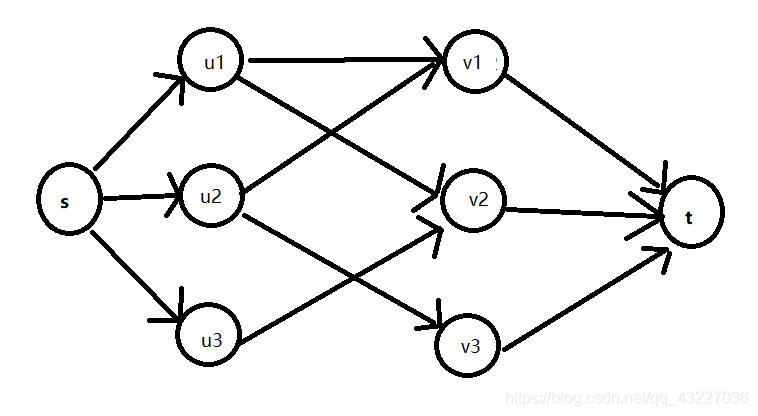
如图：

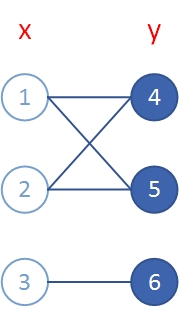
二分图非二分图

（2）代码判断：利用染色法，用两种颜色对图染色，若能全部染色没有冲突则为二分图

代码：

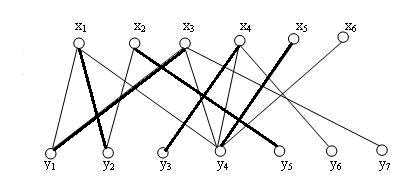
3.二分图最大匹配问题：

现在有了二分图，我们来想，假如两部分ab之间的边表示A部分的a可以和B部分的b进行配对，并且每个人只能匹配一个人，那么怎么能在不产生冲突的条件下，匹配最多的对数呢？

二.算法部分

1.匈牙利算法解决二分图最大匹配问题

（1）：https://blog.csdn.net/dark_scope/article/details/8880547

（2）实质：先到先得，能让就让；寻找增广路；

（3）增广路径的性质：

有奇数条边。

起点在二分图的左半边，终点在右半边。

路径上的点一定是一个在左半边，一个在右半边，交替出现。（其实二分图的性质就决定了这一点，因为二分图同一边的点之间没有边相连，不要忘记哦。）

整条路径上没有重复的点。

起点和终点都是目前还没有配对的点，而其它所有点都是已经配好对的。

路径上的所有第奇数条边都不在原匹配中，所有第偶数条边都出现在原匹配中。

最后，也是最重要的一条，把增广路径上的所有第奇数条边加入到原匹配中去，并把增广路径中的所有第偶数条边从原匹配中删除（这个操作称为增广路径的取反），则新的匹配数就比原匹配数增加了1个。

（4）复杂度：O（m*n）

（5）代码：HDU 2063

#include <iostream>
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1000 + 7;
bool used[maxn];
int Maching[maxn],k,n,m,tot,head[maxn];
struct Edge{int to,next;
}edge[maxn*2];
void addEdge(int a,int b){edge[tot].to = b;edge[tot].next = head[a];head[a] = tot++;
}
void init(){tot = 0;memset(head,-1,sizeof(head));memset(Maching,-1,sizeof(Maching));
}
bool DFS(int p){for(int i = head[p];~i;i = edge[i].next){int to = edge[i].to;if(!used[to]){//每试图让过used[to] = 1;//让一次if(Maching[to]==-1||DFS(Maching[to])){//没配对过/配对了但是可以让出来Maching[p] = to;Maching[to] = p;//配对成功return true;}}}return false;
}
int Hungary(int len){int sum = 0;for(int i = 1;i<=len;i++){//试图配对每一个左部分点memset(used,0,sizeof(used));if(DFS(i))sum++;//配对成功}return sum;
}
int main()
{while(scanf("%d",&k)!=EOF&&k){init();scanf("%d%d",&m,&n);for(int i = 0;i<k;i++){//k对int a,b;scanf("%d%d",&a,&b);//左部分 ---  右部分addEdge(a,m+b);//加边}int ans = Hungary(m);printf("%d\n",ans);}return 0;
}

2.匈牙利的优化算法----Hopcroft-Karp（HK）算法

参考：https://blog.csdn.net/qq_39792342/article/details/82017123

（1）思想：在匈牙利中，我们每次匹配一个点，寻找一条增广路，很浪费。我们可以在一次匹配中利用BFS尝试寻找多条增广路,然后在寻找配对时，当dist[p] ==dist[x] + 1时，p才是x的下一个增广节点。

（2）做法：BFS找增广路 + DFS进行匹配

（3）代码：HDU - 2389

#include <iostream>
#include<bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
const int maxn = 4000 + 7;
struct Node{int x,y,speed;
}node[maxn*2];
int n,m,dist[maxn*2],Maching[maxn*2];
vector<int>G[maxn];
int Length(int p,int q){return  (node[p].x - node[q].x)*(node[p].x - node[q].x) + (node[p].y - node[q].y)*(node[p].y - node[q].y);
}
bool BFS(){//寻找增广路memset(dist,-1,sizeof(dist));queue<int> que;for(int i = 1;i<=m;i++){if(Maching[i]==-1){que.push(i);dist[i] = 0;}}bool flag = false;while(!que.empty()){int p = que.front();que.pop();int len = G[p].size();for(int i = 0;i<len;i++){int to = G[p][i];if(dist[to]==-1){dist[to] = dist[p] + 1;if(Maching[to]==-1)flag = true;else {dist[Maching[to]] = dist[to] + 1;que.push(Maching[to]);}}}}return flag;
}
bool DFS(int p){//搜索匹配int len = G[p].size();for(int i = 0;i<len;i++){int to = G[p][i];if(dist[to]==dist[p] + 1){dist[to] = -1;if(Maching[to]==-1||DFS(Maching[to])){Maching[to] = p;Maching[p] = to;return true;}}}return false;
}
inline int HK(){int cnt = 0;while(BFS()){for(int i = 1;i<=m;i++){if(Maching[i]==-1&&DFS(i))cnt++;}}return cnt;
}
int main()
{int T;scanf("%d",&T);int kase = 0;while(T--){int t;memset(Maching,-1,sizeof(Maching));scanf("%d",&t);scanf("%d",&m);for(int i = 1;i<=m;i++){G[i].clear();scanf("%d%d%d",&node[i].x,&node[i].y,&node[i].speed);}scanf("%d",&n);for(int j = m+1;j<=m+n;j++){scanf("%d%d",&node[j].x,&node[j].y);for(int k = 1;k<=m;k++){int time = Length(k,j);if(time<=node[k].speed*node[k].speed*t*t)G[k].push_back(j);}}int ans = HK();printf("Scenario #%d:\n%d\n\n",++kase,ans);}return 0;
}

三.拓展部分：

1.二分图完美匹配：如果左侧部分的所有点都能够匹配，完美匹配一定是最大匹配（完美匹配的任何一个点都已经匹配，添加一条新的匹配边一定会与已有的匹配边冲突）。但并非每个图都存在完美匹配。且最大匹配不一定是完美匹配。

解决：求最大匹配，若最大匹配数==所有点数则为完美匹配

2.二分图的最小点覆盖：最小顶点覆盖：实质是个点集，点集里面的点能覆盖所有的边，最小顶点覆盖就是满足这个要求的点集中点数最小的那个。

解决：二分图的最小点覆盖 = 二分图最大匹配数

3.二分图最大独立集：实质是个点集，这个集合里的点无论怎样都两两相连不到一起，满足这个要求的点数最多的一个。也就是集合里任意两点之间无关系。

解决：二分图最大独立集 = 节点数（n）- 最大匹配数；