二分图最大匹配问题

最近在做的打车项目中，涉及到了用户叫单后，将所有出单司机和所有订单匹配的问题，借此来学习一下二分图的匹配算法。

一、无权二分图最大匹配

首先要区分一下各个概念：

匹配：图G的一个匹配是由一组没有公共端点的不是环的边构成的集合。
匹配有两个重点：1. 匹配是边的集合；2. 在该集合中，任意两条边不能有共同的顶点。
注意：二分图无奇圈。
完美匹配：考虑部集为X={x1 ,x2, …}和Y={y1, y2, …}的二分图，一个完美匹配就是定义从X-Y的一个双射，依次为x1, x2, … xn找到配对的顶点，最后能够得到 n！个完美匹配。
最大匹配：使得所有匹配中总边数最大的匹配。
注意：完美匹配一定是最大匹配，而最大匹配不一定是完美匹配。
交错路径：给定图G的一个匹配M，如果一条路径的边交替出现在M中和不出现在M中，我们称之为一条M-交错路径。
增广路径：如果一条M-交错路径，它的两个端点都不与M中的边关联，我们称这条路径叫做M-增广路径。

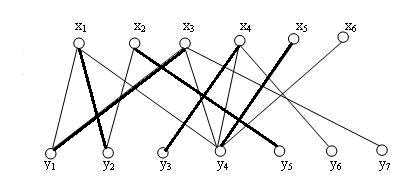
如图，这里两条加粗的边2、4是一个匹配M，而1-2-3-4-5构成一条增广路，在这条路径上，存在一个比M更大的匹配（1、3、5）

因此，我们寻找最大匹配的任务就相当于我们不断地在已经确定的匹配下，不断找到新的增广路径，因为出现一条增广路径，就意味着目前的匹配中增加一条边！
当匹配中不再存在增广路径，即说明得到了最大匹配

下面我们讨论下匈牙利算法的内容：

给定一个图：

为了得到最大匹配，我们的目标是尽可能给x中最多的点找到配对。

刚开始，一个匹配都没有，我们随意选取一条边，（x1, y1）这条边，构建最初的匹配出来，结果如下，已经配对的边用粗线标出：
在这里插入图片描述
2. 我们给x2添加一个匹配，如下图的（x2, y2）边。

我们现在想给x3匹配一条边，发现它的另一端y1已经被x1占用了，那x3就不高兴了，它就去找y1游说，让y1离开x1。

即将被迫分手的x1很委屈，好在它还有其他的选择，于是 x1 妥协了，准备去找自己看中的y2。

但很快，x1发现 y2 被x2 看中了，它就想啊，y1 抛弃了我，那我就让 y2 主动离开 x2 （很明显，这是个递归的过程）。

x2 该怎么办呢？好在天无绝人之路，它去找了y5。谢天谢地，y5 还没有名花有主，终于皆大欢喜。

匹配如下：

（x3, y1, x1, y2, x2, y5），很明显，这是一条路径P。
而在第二步中，我们已经形成了匹配M，而P原来是M的一条增广路径！

上文已经说过，发现一条增广路径，就意味着一个更大匹配的出现，于是，我们将M中的配对点拆分开，重新组合，得到了一个更大匹配，M1, 其拥有（x3, y1）,(x1, y2), (x2, y5)三条边。

而这，就是匈牙利算法的精髓：
匈牙利算法寻找最大匹配，就是通过不断寻找原有匹配M的增广路径，因为找到一条M匹配的增广路径，就意味着一个更大的匹配M’ , 其恰好比M 多一条边。

4.将x4 , x5 按顺序加入进来，最终会得到本图的最大匹配。

#include <iostream>
#include <stdio.h>
#include <cstring>
#include <vector>
#include<algorithm>using namespace std;const int maxn=10;
int map[maxn][maxn]; //邻接矩阵存图
int nx,ny;
bool vis[maxn];
int link[maxn]; // link[j]=i 表示x方i号点匹配了y方j号点int Hungarian()
{int cnt = 0;for (int i = 0; i < nx; i++){memset(vis, 0, sizeof(vis)); //每一轮都要重置vis数组if (match(i))cnt++;}return cnt;
}bool match(int i)
{for (int j = 0; j < ny; j++)if (map[i][j] && !vis[j]) //有边且未访问{vis[j] = true;                 //记录状态为访问过if (link[j] == 0 || match(link[j])) //如果暂无匹配，或者原来匹配的左侧元素可以找到新的匹配{link[j] = i;    //当前左侧元素成为当前右侧元素的新匹配return true; //返回匹配成功}}return false; //循环结束，仍未找到匹配，返回匹配失败
}int main(){int k;cin>>nx>>ny>>k;for(int i=0;i<k;i++){int x,y;cin>>x>>y;map[x][y]=1;}cout<<Hungarian();system("pause");return 0;
}

二、有权二分图最大匹配

首先要明确一下各个概念：

点标号：每一个点都有一个标号，记lx[i]为X方点i的标号，ly[j]为Y方点j的标号。
可行点标与可行边：如果对于图中的任意边(i, j, W)都有lx[i]+ly[j]>=W，则这一组点标是可行的。特别地，对于lx[i]+ly[j]=W的边(i, j, W)，称为可行边
定理：若由二分图中所有满足A[i]+B[j]=w[i,j]的边(i,j)构成的子图（称做相等子图）有完备匹配，那么这个完备匹配就是二分图的最大权匹配。

下面介绍下KM算法的内容：
KM算法的核心思想就是通过修改某些点的标号（但要满足点标始终是可行的），不断增加图中的可行边总数（可行边就是两点标号之和恰为二者边权的边），直到图中存在仅由可行边组成的完全匹配为止，此时这个匹配一定是最佳的。

求出每个点的初始标号：lx[i]=max{e.W|e.x=i}（即每个X方点的初始标号为与这个X方点相关联的权值最大的边的权值），ly[j]=0（即每个Y方点的初始标号为0）。

这个初始点标显然是可行的，并且与任意一个X方点关联的边中至少有一条可行边。
从每个X方点开始DFS增广。DFS增广的过程与最大匹配的Hungary算法基本相同，只是要注意两点：一是只找可行边，二是要把搜索过程中遍历到的X方点全部记下来（可以用vst搞一下），以进行后面的修改
增广的结果有两种：若成功（找到了增广路），则该点增广完成，进入下一个点的增广。

若失败（没有找到增广路），则需要改变一些点的标号，使得图中可行边的数量增加。方法为：在增广过程中遍历到的X方点的标号全部减去一个常数d，所有遍历到的Y方点的标号全部加上一个常数d，经过这一步后，图中至少会增加一条可行边。

d = min（lx[i]+ly[j]-W），其中i是参与此次增广过程的X点，j是未参与此次增广过程的Y点
修改后，继续对这个X方点DFS增广，若还失败则继续修改，直到成功为止

以上就是KM算法的基本思路。但是朴素的实现方法，时间复杂度为O(n4)——需要找O(n)次增广路，每次增广最多需要修改O(n)次顶标，每次修改顶标时由于要枚举边来求d值，复杂度为O(n2)。

实际上KM算法的复杂度是可以做到**O(n3)**的。我们给每个Y顶点一个“松弛量”函数slack，每次开始找增广路时初始化为无穷大。

在寻找增广路的过程中，检查边(i,j)时，如果它不在相等子图中，则让slack[j]变成原值与lx[i]+ly[j]-w[i,j]的较小值。

这样，在修改顶标时，取所有不在交错树中的Y顶点的slack值中的最小值作为d值即可。

但还要注意一点：修改顶标后，要把所有的slack值都减去d。

注意以下几点：
1，匹配两边节点不需要相等；但是需要nx<=ny
2，求最小权的时候只需要将权值取负，在求最大权即可；//十分有效
3，不存在的边权初始化为负无穷大；

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inf 100000000
using namespace std;const int maxn=100;
int map[maxn][maxn];
int nx,ny;
int link[maxn];
int visx[maxn],visy[maxn];
int lx[maxn],ly[maxn];
int slack[maxn];int KM();int main(){cin>>nx>>ny;for(int i=0;i<nx;i++)for(int j=0;j<ny;j++){cin>>map[i][j];}printf("%d\n", KM());system("pause");return 0;
}int KM() {memset(link, -1, sizeof(link));// lx 和 ly的初始化memset(ly, 0, sizeof(ly));for (int i=0; i<nx; i++) {lx[i] = -inf;for (int j=0; j<ny; j++) {lx[i] = max(lx[i], map[i][j]);}}// 从x集合的每个点寻找增广路for (int x=0; x<nx; x++) {for (int i=0; i<ny; i++) //slack 的初始化对当前点寻找增广路的左右过程中有效{ slack[i] = inf;}while(1) {memset(visx, 0, sizeof(visx));  //每次寻找增广路之前初始化memset(visy, 0, sizeof(visy));if (dfs(x)) break; //该点增广完成// 否则修改可行顶标int d = inf;for (int i=0; i<ny; i++) {if (!visy[i])d = min(d, slack[i]);}for (int i=0; i<nx; i++) {if (visx[i]) lx[i] -= d;}for (int i=0; i<ny; i++) {if (visy[i]) ly[i] += d;else slack[i] -= d;}}}int res = 0;for (int i=0; i<ny; i++) { //必定已经找到一个所有相等子图的点导出的完美匹配if (link[i] != -1)res += map[link[i]][i]; // 右集合i的匹配点link[i] 这里不像无向图那样，需要注意顺序---------}return res;
}bool dfs(int x) {visx[x] = 1;  // 左集合访问到的点一定都在交错树中for (int i=0; i<ny; i++) {if (visy[i]) continue;int w = lx[x] + ly[i] - map[x][i];if (w == 0) //可行边{visy[i] = 1;  // 右集合的点在相等子图中 就一定在交错树中if (link[i] == -1 || dfs(link[i])) {link[i] = x;return 1;}}else slack[i] = min(slack[i], w); // 修改不在相等子图中的点的slack值}return 0;
}