二分图最大匹配问题（匈牙利算法）

article/2025/9/17 10:09:14

什么是二分图

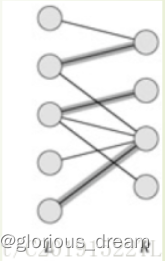
如果一个无向图的的顶点可以分为两个互不相交的子集A和B，那么它就是二分图。也就是说，A、B内部不存在连边，所有连边都一头连着A中的顶点，另一头连着B中的顶点。

什么是二分图最大匹配？

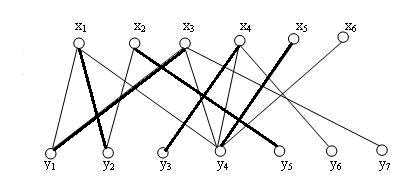
二分图最大匹配问题，就是在A、B这两个集合中，不断选择两个存在连线的点，把他们连起来，求最多可以有多少条连线的问题。

怎么解？

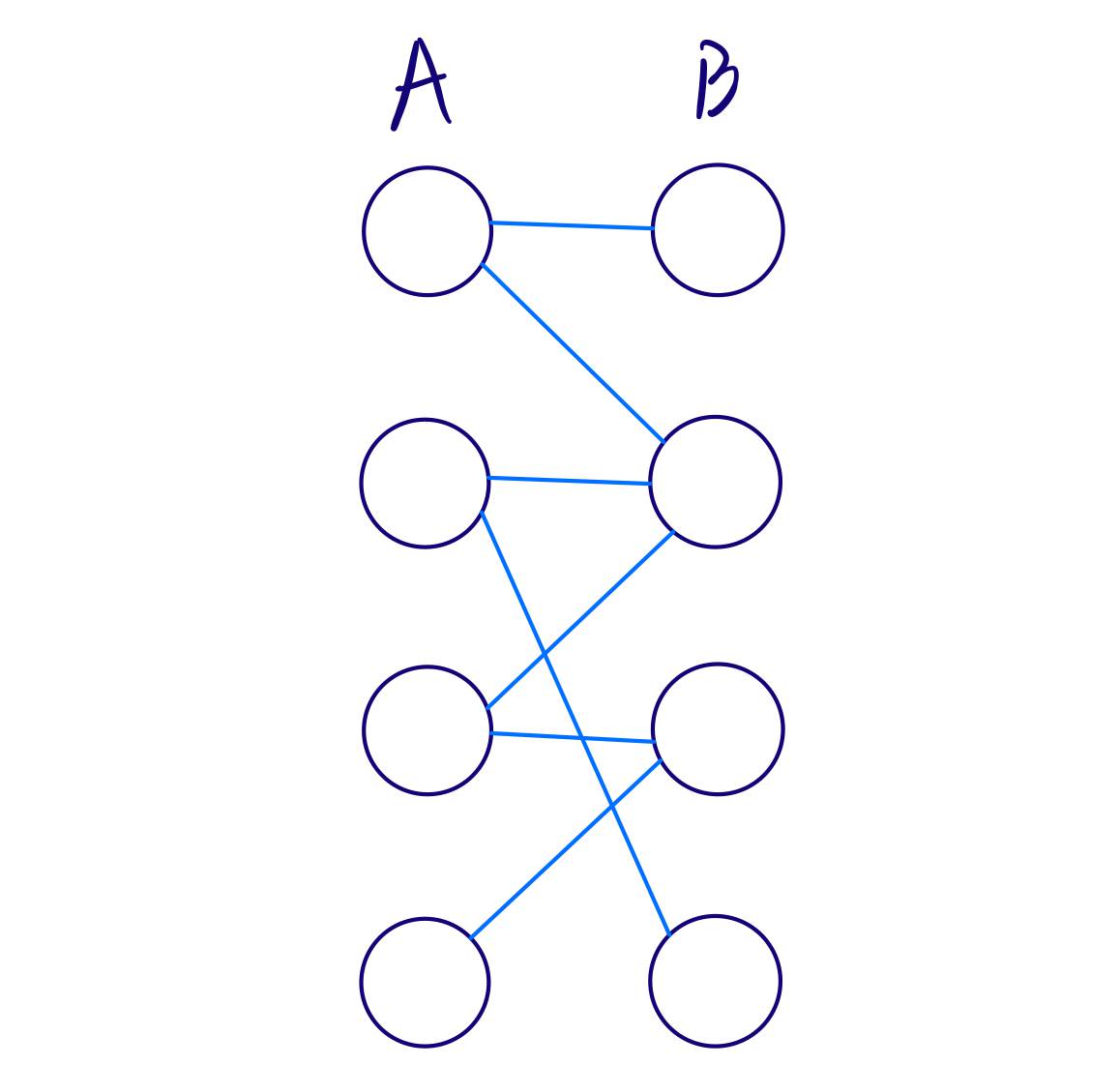
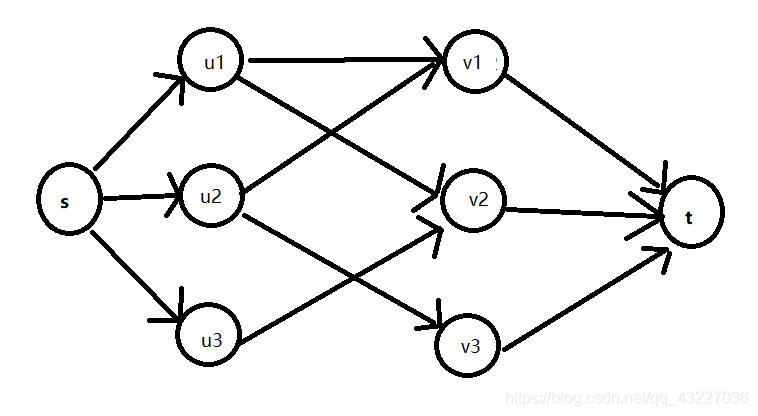
匈牙利算法的核心在于：从A集合中选择一个点，然后将与其相连的B中的点依次对照，如果B中的点尚未匹配，那就将这两个点进行匹配，然后遍历A中的下一个点。接着继续访问与其相连的B中的点，如果B中的点已经被匹配了，那就尝试递归地将与B中的这个点相匹配的A中的点换一个匹配对象（递归地执行上述过程）。这其实就是在寻找增广路。当找到一条增广路，就能使得匹配数+1。如此一来，当我们把A中的所有点遍历之后，就能得到最大的匹配了。

上面这个过程说起来有点绕口，我也想了很久才想明白。

在敲代码的时候还要注意一点，我们一直都是对于A中的点进行DFS，而被访问到的B中的点，需要在被访问到的时候，设置vis为true，否则会造成死循环。

上面说的“对A中的点进行DFS”怎么理解呢？由于增广路是：未匹配边-匹配边-未匹配边-匹配边-未匹配边，即开头结尾都要是未匹配边，因此我们设定A集合出发的边都是未匹配边，B集合出发的都是匹配边。然后，由于匹配边是确定的，因此在寻找增广路时，不需要对B中的点进行DFS，只需将与B点匹配的A中的点进行DFS即可，这样才能满足增广路的要求。

题目

这是一道模板题：https://uoj.ac/problem/78

从前一个和谐的班级，有 nl 个是男生，有 nr 个是女生。编号分别为 1,…,nl 和 1,…,nr。有若干个这样的条件：第 v 个男生和第 u 个女生愿意结为配偶。请问这个班级里最多产生多少对配偶？输入格式
第一行三个正整数，nl,nr,m。接下来 m 行，每行两个整数 v,u 表示第 v 个男生和第 u 个女生愿意结为配偶。保证 1≤v≤nl，1≤u≤nr，保证同一个条件不会出现两次。输出格式
第一行一个整数，表示最多产生多少对配偶。接下来一行 nl 个整数，描述一组最优方案。第 v 个整数表示 v 号男生的配偶的编号。如果 v 号男生没配偶请输出 0。样例一
input
2 2 3
1 1
1 2
2 1output
2
2 1explanation
1 号男生跟 2 号女生幸福地生活在了一起～2 号男生跟 1 号女生幸福地生活在了一起～样例二
input
2 2 2
1 1
2 1output
1
1 0explanation
班上一个女神一个女汉子，两个男生都去追女神。一种最优方案是：1 号男生跟 1 号女生幸福地生活在了一起～2 号男生孤独终生。= =||限制与约定
1≤nl,nr≤500，1≤m≤250000。时间限制：1s
空间限制：256MB

这很明显是一个二分图最大匹配问题，由于男生女生的编号都是从1开始，因此为了能便于区分，我们将女生的编号x暂时设置为x+nl，这样就能保证每个人编号的唯一性。

代码如下：

//二分图最大匹配
#include <bits/stdc++.h>
using namespace std;#define MAXN 505
#define INF (1 << 31)bool vis[MAXN * MAXN];
int nl, nr, m;
int girl[MAXN];
int match[MAXN * 3];struct edge
{int from, to, next = 0;
} e[MAXN * MAXN];int head[3 * MAXN];
int js_edges = 0;void add(int u, int v)
{e[++js_edges].from = u;e[js_edges].to = v;e[js_edges].next = head[u];head[u] = js_edges;
}bool dfs(int x)
{vis[x] = true;//cout << "x " << x << endl;int nd = head[x];while (nd != 0){if (!vis[e[nd].to]){vis[e[nd].to]=true;//防止来回横跳，无法退出//cout << "     " << e[nd].to << endl;if (!match[e[nd].to] || dfs(match[e[nd].to])){match[x] = e[nd].to;match[e[nd].to] = x;return true; //找到增广路或者能够创建连线}}nd = e[nd].next;}return false;
}int main()
{scanf("%d%d%d", &nl, &nr, &m);int v, u;for (int i = 0; i < m; ++i){scanf("%d%d", &v, &u);//人的id划分：男生都加nr， 女生不变add(v, u + nl);}int ans = 0;for (int i = 1; i <= nl; ++i){memset(vis, 0, sizeof(vis));if (dfs(i))++ans;}printf("%d\n", ans);for (int i = 1; i <= nl; ++i){if (match[i] == 0)printf("0 ");elseprintf("%d ", match[i] - nl);}printf("\n");
}

转载请注明原文：https://www.longjin666.top/?p=1122