文章目录
- AOV网
- 拓扑排序算法
- 实现步骤
- 代码实现
AOV网
- 在一个工程的有向图中,用顶点表示活动,用弧表示活动之间的优先关系,这样的有向图为顶点表示活动的网,我们称为AOV网(Activity on Vertex Network)。AOV网中的弧表示活动之间存在的某种制约关系。并且AOV网中不能存在环路,即某个活动的开始不可能以自己的完成作为先决条件。
- 设G=(V, E)是一个具有n个顶点的有向图,V中的顶点序列V1,V2,V3…Vn,满足若从顶点Vi到Vj有一条路径,则在顶点序列中顶点Vi必在顶点Vj之前。我们称这样的顶点序列为一个拓扑序列。
- 拓扑排序其实就是对一个有向图构造拓扑序列的过程。

拓扑排序算法
实现步骤
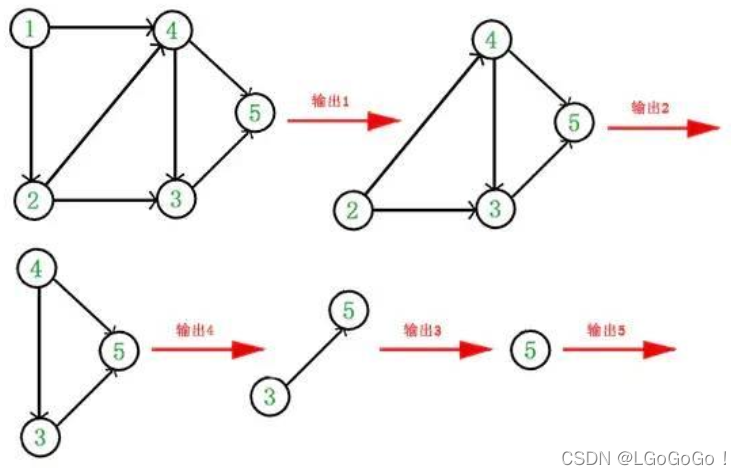
对AOV网进行拓扑排序的基本思路是:从从AOV网中选择一个入度为0的顶点输出,然后删去此顶点,并删除以此顶点为尾的弧,继续重复此步骤,直到全部顶点或者AOV网中不存在入度为0的顶点为止。
代码实现
/** @Author: Xyh4ng* @Date: 2022-11-24 10:46:58* @LastEditors: Xyh4ng* @LastEditTime: 2022-11-24 13:57:10* @Description:* Copyright (c) 2022 by Xyh4ng 503177404@qq.com, All Rights Reserved.*/
#include <stdio.h>
#include <stdlib.h>#define MAXSIZE 500typedef struct
{int vexs[MAXSIZE];int arc[MAXSIZE][MAXSIZE];int numVertexes, numEdges;
} MGraph;// 边表结点
typedef struct EdgeNode
{int adjVex;int weight;struct EdgeNode *next;
} EdgeNode;// 顶点表结点
typedef struct VertexNode
{int in;int data;EdgeNode *firstEdge;
} VertexNode, AdjList[MAXSIZE];typedef struct GraphAdjList
{AdjList adjList;int vertexNums, edgeNums;
} GraphAdjList;// 构建图
void CreateMGraph(MGraph *G)
{G->numVertexes = 14;G->numEdges = 20;for (int i = 0; i < G->numVertexes; i++){G->vexs[i] = i;}for (int i = 0; i < G->numVertexes; i++){for (int j = 0; j < G->numVertexes; j++){G->arc[i][j] = 0;}}G->arc[0][4] = 1;G->arc[0][5] = 1;G->arc[0][11] = 1;G->arc[1][2] = 1;G->arc[1][4] = 1;G->arc[1][8] = 1;G->arc[2][5] = 1;G->arc[2][6] = 1;G->arc[2][9] = 1;G->arc[3][2] = 1;G->arc[3][13] = 1;G->arc[4][7] = 1;G->arc[5][8] = 1;G->arc[5][12] = 1;G->arc[6][5] = 1;G->arc[8][7] = 1;G->arc[9][10] = 1;G->arc[9][11] = 1;G->arc[10][13] = 1;G->arc[12][9] = 1;
}// 利用邻接矩阵构建邻接表
void InitGraphADjList(MGraph *G, GraphAdjList *GL)
{GL->vertexNums = G->numVertexes;GL->edgeNums = G->numEdges;for (int i = 0; i < G->numVertexes; i++) /* 读入顶点信息,建立顶点表 */{GL->adjList[i].in = 0;GL->adjList[i].data = G->vexs[i];GL->adjList[i].firstEdge = NULL; /* 将边表置为空表 */}for (int i = 0; i < G->numVertexes; i++) /* 建立边表 */{for (int j = 0; j < G->numVertexes; j++){if (G->arc[i][j] == 1){EdgeNode *e = (EdgeNode *)malloc(sizeof(EdgeNode));e->adjVex = j; /* 邻接序号为j */e->next = GL->adjList[i].firstEdge; /* 将当前顶点上的指向的结点指针赋值给e */GL->adjList[i].firstEdge = e; /* 将当前顶点的指针指向e */GL->adjList[j].in++;}}}
}int TopologicalSort(GraphAdjList *GL)
{int count = 0; // 用于统计输出顶点的个数// 用于存放入度为0的顶点int *stack = (int *)malloc(sizeof(int) * GL->vertexNums);int top = 0;// 入度为0的顶点入栈for (int i = 0; i < GL->vertexNums; i++){if (GL->adjList[i].in == 0){stack[++top] = i;}}while (top != 0){// 栈顶出栈并将其邻接结点入度-1int k = stack[top--];printf("%d, ", GL->adjList[k].data);count++;EdgeNode *p = GL->adjList[k].firstEdge;while (p != NULL){GL->adjList[p->adjVex].in--;// 顶点入度只会在这里变化,因此在此处判断入度是否为0if (GL->adjList[p->adjVex].in == 0){stack[++top] = p->adjVex;}p = p->next;}}if (count < GL->vertexNums) // 若输出的顶点个数少了,则说明这个网存在环路,不是AOV网return 0;elsereturn 1;
}int main()
{MGraph *G = (MGraph *)malloc(sizeof(MGraph));CreateMGraph(G);GraphAdjList *GL = (GraphAdjList *)malloc(sizeof(GraphAdjList));InitGraphADjList(G, GL);int flag = TopologicalSort(GL);return 0;
}