本文主要对正态性检验方法做了汇总，重点阐述了常用的正态性检验方法的使用场景及其在 R 或 Python 中的实现。

0.概述

正态分布在统计学中有着极为重要的地位，它是${\chi }^2$分布、$t$分布、$F$分布的基础，也是许多统计方法的理论基础，故检验样本是否来自正态分布具有十分重要的意义。
正态性检验的方法有很多，以下列举了一些常见的方法：

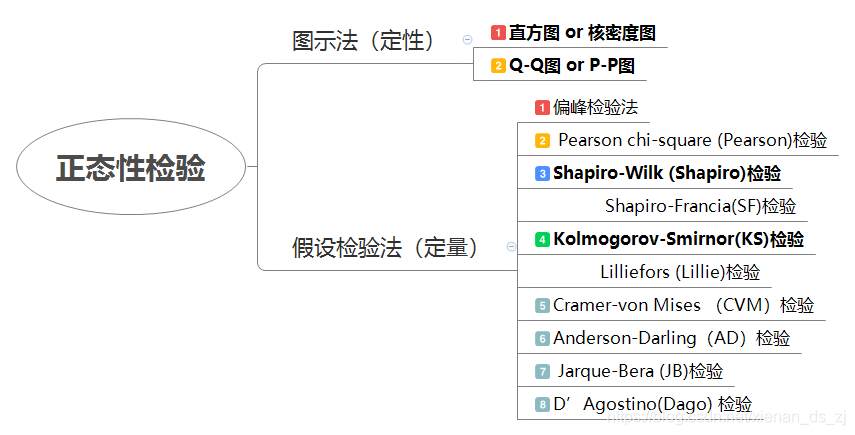
对于正态性检验，建议首先利用直方图或核密度估计得到样本数据的分布图，若分布严重偏态或尖峰，可认为其不是来自于正态分布；若根据直方图或核密估计分布不容易做出判断，再利用各检验方法对其检验。
注意：对于正态性检验，应该避免仅根据一种检验方法便轻易的做出决策，应该使用多种方法，综合评价。 source:参考文献[1]

另还有一些选择正态性检验的规定，仅供参考：

• SPSS 规定：当样本含量 3≤n≤5000 时，结果以 Shapiro—Wilk(W 检验) 为准，当样本含量 n>5000 结果以 Kolmogorm —Smimov(D 检验，修正后的KS检验，即Lillie检验，见2.2.3) 为准。
• SAS 规定：当样本含量 n≤2000 时，结果以 Shapim—Wilk(W 检验) 为准，当样本含量 n>2000 时，结果以 Kolmogorov—Smimov(D 检验，修正后的KS检验) 为准。

下文对直方图、Q-Q图以及Shapiro检验、KS检验的原理做一个较为详细的叙述，并给出对应方法在R语言和Python中的实现。另外，对其余方法做简要叙述。

本文内容中理论部分是作者阅读文献后整理得到

1.图示法

1.1 直方图

1.1.1 介绍

直方图(histogram)是用于展示分组数据分布的一种图形，它是用矩形的宽度和高度（即面积）来表示频数分布的。绘制该图时，在平面直角坐标系中，用横轴表示数据分组，纵轴表示频数或频率，这样就形成了一个矩形（即直方图）。
直方图与柱状图的区别：①直方图的高度与宽度都有意义。柱状图是用柱子的长度表示各类别频数的多少，其宽度（表示类别）固定；而直方图是用面积表示各组频数的多少，矩形的高度表示每一组的频数或频率，宽度则表示各组的组距；②由于分组数据具有连续性，直方图的各矩形通常是连续排列，而柱状图则是分开排列；③柱状图用于展示分类型数据，直方图用于展示数值型数据。source:参考文献[2]
直方图的具体绘制方法见参考文献[3] $p_{15}$

1.1.2 直方图初判

1.2 Q-Q图检验法（直线检验法）

1.2.1 Q-Q图性质

假设样本$X_1,X_2,...,X_n$来自正态总体$N(\mu ,{\sigma }^2)$. 将样本观测值按照由小到大的顺序排列, 得到次序统计量$x_{(1)}\le x_{(2)}\le \cdot \cdot \cdot \le x_{(n)}$和经验分布函数

$$F_n(x)=\{\begin{array}{rcl}0& & x<x_{(1)}\\ k/n& & x_{(k)}\le x\le x_{(k+1)},k=1,2,...,n\\ 1& & x\ge x(n)\end{array}$$
由于当$n$充分大时，$\forall \epsilon >0$有$P(|F_n(x)-F(x)|>\epsilon )=0$.
又$F(x)=P(X\le x)=\varphi (\frac{x-\mu }{\sigma })$
故当$n$充分大时，$F_n(x)=\varphi (\frac{x-\mu }{\sigma })$, $a.s$
即$\frac{x-\mu }{\sigma }={\varphi }^{(-1)}(F_n(x)),a.s$
$\forall x\in R$, 令${\varphi }^{-1}(F_n(x))\equiv \omega$, 则有
$$x\equiv \sigma \omega +\mu ,a.s$$
上式意味着，当总体是$N(\mu ,{\sigma }^2)$且样本量$n$充分大时，样本观测值$x$和逆标准正态分布值$\omega$组成的点$(\omega ,x)$几乎处于一条直线上. source: 参考文献[3] $p_{22}$

1.2.2 作Q-Q图的步骤

1. 将原始数据按升序排序，得到次序统计量$x_{(1)}\le x_{(2)}\le \cdot \cdot \cdot \le x_{(n)};$
2. 计算与$x_{(n)}$相应的事件$X\le x_{(n)}$的概率(每个数据对应的百分位数)
   $$p_i=F_n(x_{(n)})=\frac{i-0.5}{n};$$
3. 对概率$p_i$计算相应的标准正态分位数$u_i(i=1,2,...,n);$
4. 把点$(u_i,x_{(i)})$画在平面直角坐标系上，并考察它们是否在一条直线上；
5. #计算相关系数
   $$r=\frac{\sum (x_{(i)}-\overline{x})(u_i-\overline{u})}{\sqrt{\sum (x_{(i)}-\overline{x}{)}^2}\sqrt{\sum (u_i-\overline{u}{)}^2}}$$
   并检验其正态性（若点$(u_i,x_{(i)})$近似在一条直线上（相关系数r=…），故可认为样本来自正态总体）

1.2.3 Q-Q图实现

• R

library(car)
qqnorm(x)

• Python

# QQ图
import statsmodels.api as sm
sm.qqplot(y,line='s')# PP图
from scipy import stats
stats.probplot(x, dist="norm", plot=plt)

1.3 其他图示法

• 核密度图判断该样本是否来自正态总体与直方图类似。
• P-P图见参考文献[3] $p_{24}$

2.假设检验法

建立假设
$H_0:$总体$X$的分布为正态分布$N(\mu ,{\sigma }^2)$；(样本来自总体与正态分布无显著差异，即符合正态分布)
$H_1:$总体$X$的分布不是正态分布$N(\mu ,{\sigma }^2)$

2.1 Shapiro-Wilk检验（Shapiro）

W 检验全称 Shapiro-Wilk 检验，是一种基于相关性的算法。计算可得到一个相关系数，它越接近 1 就越表明数据和正态分布拟合得越好。

2.1.1 检验步骤

1. 将原始数据按升序排序，得到次序统计量$x_{(1)}\le x_{(2)}\le \cdot \cdot \cdot \le x_{(n)};$
2. 构造统计量
   $$W=\frac{({\sum }_{i=1}^n{a}_i{x}_i{)}^2}{{\sum }_{i=1}^n(x_i-\overline{x}{)}^2};$$

注：这里， $x_i$是第 i 个顺序统计量，即第 i 个最小的样本观测值。
$a_i , i=1,2…,n $是常数，它们的定义为
$$(a_1,...,a_n)=\frac{m^T{V}^{-1}}{(m^T{V}^{-1}{V}^{-1}m{)}^{1/2}}$$
$m=(m_1,...,m_n{)}^T$ 是样本顺序统计量的样本均值， V是样本
顺序统计量的协方差矩阵。
(a可直接查表得到)

3. 计算检验统计量$W$，并与判断临界值$W_{\alpha }$做比较。
4. 得出结论:若 $W<W_{\alpha }$，按表上行写明的显著性水平α舍弃正态性假设($H_0$),若 $W>W_{\alpha }$, 接受正态性假设.

2.1.2 实现

• R

shapiro.test(x)

• Python

from scipy import statsstats.shapiro(x)

2.2 Kolmogorov-Smirnor检验（KS）

KS检验基于经验分布函数，该检验用大样本近似。其检验的是标化后的数据是否服从理论的分布。
需要注意的是样本数据如果有结点（及是重复的数据），则无法计算准确的P值。

2.2.1 KS检验步骤

设样本的经验概率分布函数定义为$F_n(x)=\frac{1}{n}{\sum }_{i=1}^n{I}_{X_i\le x}$，若$X_i\le 1$ 则$I_{X_i\le x}=1$，否则0.

1. 构造统计量（样本的累计分布函数与理论分布的分布函数的最大值）
   $$D_n=\underset{x}{\sup }|F_n(x)-F(x)|$$
2. 计算检验统计量$D_n$的值，拒绝域或者 p- 值由 K-S 分布计算给出。

$D_n$的计算:
1)计算原数据的均值$\overline{x}$与标准差$s$，以及各水平对应的频数；
2)对水平的大小排序，得到频数序列，计算累计频数；
3)再计算累计频率，以及对应水平用Z-score法标准化后的取值；
4)使用标准化后的取值$x$，查表得到理论分布的值；
5)$D_n=max(累计频率-理论分布)$
D值越小越接近正态分布

2.2.2 KS检验实现

• R

ks.test(x, "pnorm",mean(x),sd(x))
#x为要检验的样本数据，其函数默认修改的精确公式、双边检验。
#需要大样本近似命令中加exact = F；
#单边我们可以用alternative = "less"或alternative= "greater"选择。

• Python

from scipy import statsstats.kstest(x, 'norm', (x.mean(), x.std()))  # 注意，Python的ks检验其P-value有时会与其他统计软件略微不同

2.2.3 Lilliefors检验(K-S检验的修正)

Lilliefors (Lillie)检验最早由Lilliefors 于1967年提出，它是对KS正态性检验的的修正，适合大样本。
适用于一般的正态性检验。
Lillie检验实现：

library(nortest)lillie.test(x)

# Python中未找到lillie检验的封装函数.

2.3 其他检验法

• 偏峰检验法
  详见参考文献[3] $p_{21}$
• Pearson chi-square (Pearson)检验
  R nortest包中pearson.test()可以实现
  详见参考文献[3] $p_{20}$ [4][1]
• Cramer-von Mises （CVM）检验
  R中nortest 包中的cvm.test()可以实现)，需要注意的是如果（1+0.5/n）W的值不能大于2.64
  详见参考文献[4][1]
• Anderson-Darling（AD）检验
  R中nortest包中的ad.test()可以实现
  详见参考文献[4][1]
• Jarque-Bera (JB)检验（时间序列中常用）
  Python实现：

import scipy.stats as ss
ss.jarque_bera(y)

https://www.php.cn/python-tutorials-391980.html
R中可用tseries包中的jarque.bera.test()实现
详见参考文献[4][1]

• D’Agostino(Dago) 检验
  R的fBasics包中 dagoTest()可以实现
  详见参考文献[1]
• Shapiro-Francia(SF)检验
  R中nortest包，sf.test()实现。是Shapiro检验的修正。
  详见参考文献[1]

还可以参考：
https://blog.csdn.net/u013524655/article/details/41053045 （SPSS）
http://www.mamicode.com/info-detail-937349.html （R）https://blog.csdn.net/cyan_soul/article/details/81236124 （Python）

参考文献：
[1] 何凤霞,马学俊. 基于R软件的正态性检验的功效比较[J].统计与决策,2012(18):17-19.
[2] 贾俊平. 统计学[M]. 第6版. 北京：中国人民大学出版社, 2014.12
[3] 高慧璇. 统计计算[M]. 北京：北京大学出版社, 1995.
[4] 李洪成. 数据的正态性检验方法及其统计软件实现 [J]. 统计与决策, 2009(12):155-156.