第五章函数和代码的复用

5.1 函数的定义与使用

5.1.1 函数的理解和定义

函数是一段代码的表示：
函数是IPO的实现
函数是一段代码的封装
①特定功能、可重用的语句组
②功能的抽象
#作用：降低编程难度、代码复用
def <函数名> ( <变量> ) :
<语句块>
return <返回值>

5.1.2 函数的使用及调用过程

定义时不被执行，调用时给定参数取代占位符

5.1.3 函数的参数传递

参数个数：0~n
（1）可选参数传递
def <函数名> ( <不可选参数> ，<可选参数>) :
<语句块>
return <返回值>
#如过在调用函数时给了可选参数的实际值，则继续
#如过在调用函数时没给可选参数的实际值，则使用定义时给出的默认值
（2）可变参数传递
def <函数名> ( <参数> ，*b) :
<语句块>
return <返回值>
注：*b的意思是表达不确定参数
（3）参数传递的两种方式
①位置传递
②名称传递

5.1.4 函数的返回值

函数可以有0~n个返回值，不确定使用return

5.1.5 局部变量和全局变量

（1）局部变量和全局变量是不同的变量
global <变量>：说明在本函数中使用的该变量为全局变量
（2）局部变量为组合数据类型且未创建，等同于全局变量
局部变量为组合数据类型，在函数中创建，运行结束后被释放

5.1.6 lambda函数

lambda函数返回函数名作为结果（函数的紧凑表达）
<函数名>：lambda <参数>：<表达式>

5.2 七段数码管绘制

（1）模块化思维：确定模块接口，封装功能
（2）规则化思维：过程抽象为规则，计算机自主判断
（3）化繁为简：多种功能的组合
代码优化过程：
单个数字的每一笔
完整的单个数字
根据输入时间输出8个数字
数字笔画间隔以美化
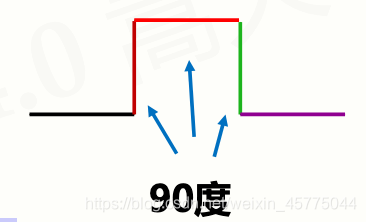
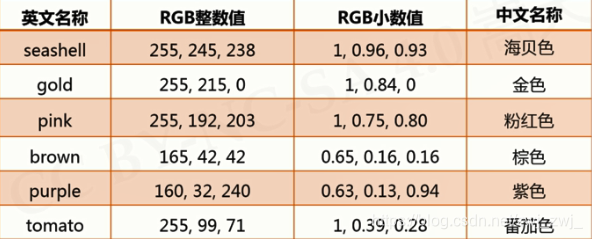
输出年月日的标识，并颜色区分
取得系统时间，格式化输出

#七段数码管
import turtle,time
def drawGap():    #绘制数码管间隔以美化turtle.penup()turtle.fd(5)def drawLine(draw):    #绘制单段数码管的每一笔drawGap()turtle.pendown() if draw else turtle.penup()turtle.fd(40)drawGap()turtle.right(90)def drawDigit(digit):    #根据数字绘制单个数码管drawLine(True) if digit in [2,3,4,5,6,8,9] else drawLine(False)drawLine(True) if digit in [0,1,3,4,5,6,7,8,9] else drawLine(False)drawLine(True) if digit in [0,2,3,5,6,8,9] else drawLine(False)drawLine(True) if digit in [0,2,5,6,8] else drawLine(False)turtle.left(90)drawLine(True) if digit in [0,4,5,6,8,9] else drawLine(False)drawLine(True) if digit in [0,2,3,5,6,7,8,9] else drawLine(False)drawLine(True) if digit in [0,1,2,3,4,7,8,9] else drawLine(False)turtle.left(180)turtle.penup()turtle.fd(20)def drawDate(date):     #根据数字绘制数码管for i in date:if i=='-':turtle.write('年',font=("Arial",18,"normal"))turtle.pencolor("green")turtle.fd(40)elif i=='=':turtle.write('月',font=("Arial",18,"normal"))turtle.pencolor("blue")turtle.fd(40)elif i=='+':turtle.write('日',font=("Arial",18,"normal"))else:drawDigit(eval(i))def main():    #main函数turtle.setup(800,350,200,200)turtle.penup()turtle.fd(-300)turtle.pensize(5)drawDate(time.strftime('%Y-%m=%d+',time.gmtime()))turtle.hideturtle()    #隐藏海龟（那个点点）turtle.done()main()

5.3代码复用与函数递归

5.3.1 代码复用与模块化设计

代码复用：函数和对象、资源化和抽象化
模块化设计：通过函数或对象封装将程序划分为模块或模块间的表达（分而治之、分层抽象、体系化）
模块内部紧耦合，模块之间松耦合

5.3.2 代码复用与函数递归

函数递归：在函数定义中调用函数自身
递归：链条与基例
数学归纳法

5.3.3 函数递归的调用过程

递归的实现
递归本身是一个函数，需要用函数定义方式描述
函数内部，采用分支语句对输入参数进行判断
基例和链条，分别编写对应代码

5.3.4 函数递归实例

（1）字符串反转输出函数

def rvs(s):if s == "":return selse :return rvs(s[1:])+s[0]

（2）斐波那契数列函数

def f(n):if n==1 or n==2:return 1else:return f(n-1)-f(n-2)

（3）汉诺塔问题函数

count=0
def hanoi(n,src,dst,mid):global countif n==1:print("{}:{}->{}".format(1,src,dst))count+=1else:hanoi(n-1,src,mid,dst)print("{}:{}->{}".format(1,src,dst))count+=1hanoi(n-1,src,mid,dst)
hanoi(3,"a","b","c")
print(count)

5.4 PyInstaller库的使用

常用参数
在这里插入图片描述

5.5 科赫雪花小包裹

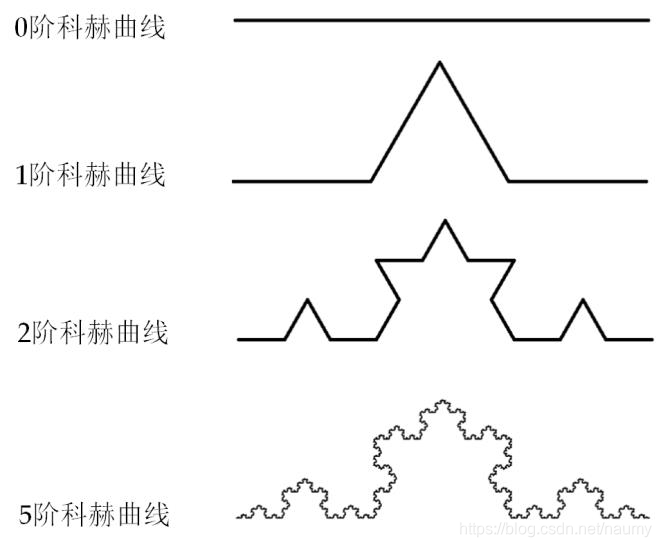
分形几何、科赫曲线、雪花曲线、迭代关系
（1）三阶科赫曲线

#KochDraw.py
import turtle
def koch(size,n):if n == 0:turtle.fd(size)else :for angle in [0,60,-120,60]:turtle.left(angle)koch(size/3,n-1)
def main():turtle.setup(800,400)turtle.penup()turtle.goto(-300,-50)turtle.pendown()turtle.pensize(2)koch(600,3)turtle.hideturtle()
main()

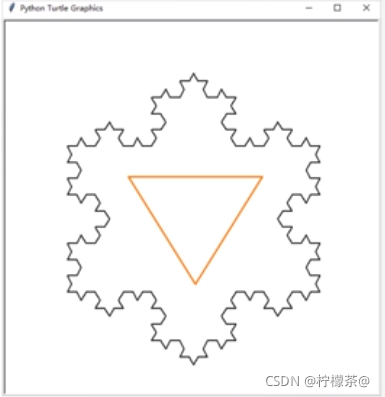
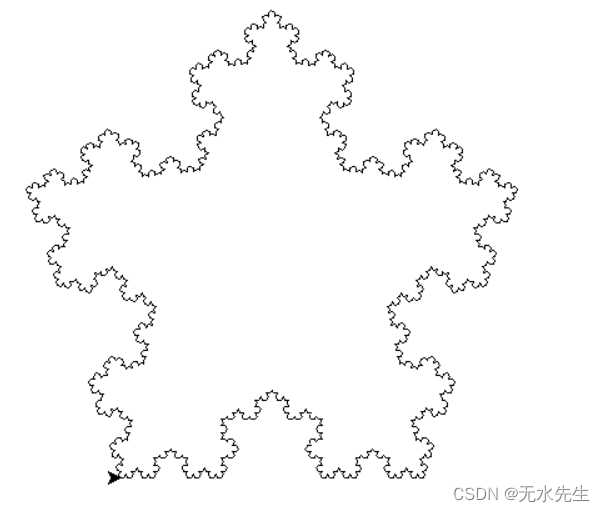
（2）科赫雪花
打包操作：pyinstaller -i curve.ico -F KochDrawV2.py
绘制阶数、科赫曲线的基本定义及角度、基础框架图形
康托尔集、谢尔宾斯基三角形、门格海绵
龙形曲线、空间填充曲线

#KochDraw.py
import turtle
def koch(size,n):if n == 0:turtle.fd(size)else :for angle in [0,60,-120,60]:turtle.left(angle)koch(size/3,n-1)
def main():turtle.setup(600,600)turtle.penup()turtle.goto(-200,100)turtle.pendown()turtle.pensize(2)level = 3koch(400,level)turtle.right(120)koch(400,level)turtle.right(120)koch(400,level)turtle.hideturtle()
main()