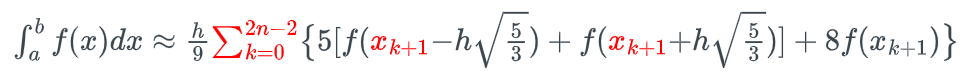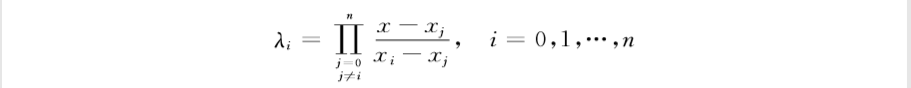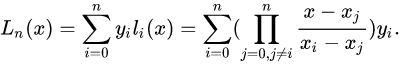局域网下Mac和Windows共享文件夹share

工作原因，一台windows10电脑，一台MacOS12.0，经常需要在两台设备之间互相传输文件，每次都用U盘拷贝很麻烦，有的时候文件太大根本无法拷贝就很尴尬。于是就参考网络上的各路大神，实现在局域网下Mac和Windows之间建立共享文件夹share，参考链接：局域网下Mac和Windows共享文件夹
作者：4ea0af17fd67，再次感谢大佬。

首先需要确定一点，就是需要互传文件的Mac和PC都是在一个路由器组成的局域网下(意思就是两台设备都连接同一个Wi-Fi)。

具体步骤：
1、首先在WINS设备上选择一个比较大的分区建立一个名字叫做“share”的共享文件夹(选择一个大分区是为了以后共享传输大文件比较方便)；比如我的放在F盘下：

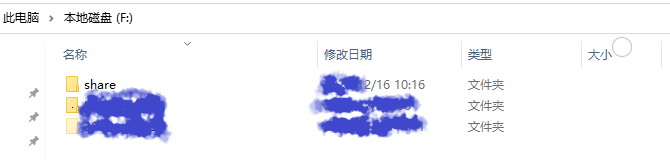
2、将共享文件夹的用户(你自己的用户、Administer、Everyone、Guest等)权限全部设定为完全控制，设置的时候时候是否需要密码就看各自需要了；
tips：share->右键属性->共享->高级共享(D)…->勾选共享此文件夹->权限，完全控制，更改，读取三个选项根据自己的需求勾选。

3、假定你的WINS设备在局域网中的名字是“MyStupid-PC”，（注：在上图左侧图中“网络路径”处可以看到自己wins设备在局域网中的名字）那么现在打开Mac中的Safari浏览器，在地址栏中输入“smb://MyStupid-PC/share”，这时如果在Wins设备上的共享文件夹权限设置没有问题，会提示请输入服务器名称和密码，之后分别输入Wins设备的账户名和登录密码，那么你可以看到已经在Mac上打开了共享文件夹share，同时在Mac桌面上也会显示一个名字为“share”的磁盘图标(我的Mac在桌面就没显示，尴尬，可能是系统版本不一样，但可以在访达->位置处显示一个与上述网络路径同名的一个设备，点开该设备能够看到share文件夹，所以下面的第4、5步直接跳过，来到了第6步，说明成功啦)。
Mac端访问tips:访达->前往->连接服务器->sub://网络路径下的名称->连接->输入Wins设备的账户和密码

4、鼠标右键点击(或按住花键点击)Mac桌面上的名字为“共享”的磁盘图标，在弹出的菜单中选择“制作替身”。

5、或者把这个share文件夹放在finder左边的快捷访问中，这样就能随时访问了。

6、 到此全部操作就完成了，以后只要在局域网络状态正常且PC开机的状态下，就可以打开共享文件夹，Mac和PC之间互传文件就没有任何问题了，直接把需要传输的文件拷贝到share文件夹下就可以在另一台设备的share文件夹下看到拷贝的文件了，又快又简单，而且不受文件大小的控制(只要共享文件夹所在的分区容量够大)。

原理是使用smb协议，共享了文件夹，需要在同一局域网下，所以记得连接同一个局域网，如果网络断了请及时连接，否则share将无法使用。