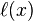一．线性插值(一次插值）
    已知函数f(x)在区间[xk ,xk+1 ]的端点上的函数值yk =f(xk ), yk+1 = f(xk+1 ),求一个一次函数y=P1 (x)使得yk =f(xk ),yk+1 =f(xk+1 ), 其几何意义是已知平面上两点(xk ,yk ),(xk+1 ,yk+1 ),求一条直线过该已知两点。

    1. 插值函数和插值基函数
由直线的点斜式公式可知： 

          

把此式按照 yk 和yk+1 写成两项:
          
记
          
并称它们为一次插值基函数。该基函数的特点如下表： 
          
从而
         P1 (x) = yk lk (x) + yk+1 lk+1 (x)

此形式称之为拉格朗日型插值多项式。其中, 插值基函数与yk 、yk+1 无关，而由插值结点xk 、xk+1所决定。一次插值多项式是插值基函数的线性组合, 相应的组合系数是该点的函数值yk 、yk+1 .

例1: 已知lg10=1,lg20=1.3010, 利用插值一次多项式求lg12的近似值。

解: f(x)=lgx,f(10)=1,f(20)=1.3010,设
          x0 =10 ,x1 =20 ,y0 =1 ,y1 =1.3010
则插值基函数为：
          
于是, 拉格朗日型一次插值多项式为:
          
故 :
          
即lg12 由lg10和lg20 两个值的线性插值得到,且具有两位有效数字(精确值lg12=1.0792).

    二．二次插值多项式
    已知函数y=f(x)在点xk-1 ,xk ,xk+1上的函数值yk-1 =f(xk-1 ),yk =f(xk ), yk+1 =f(xk+1 ), 求一个次数不超过二次的多项式P2(x), 使其满足,

             P2 (xk-1 )=yk-1 , P2 (xk )=yk , P2 (xk+1 )=yk+1 .

其几何意义为:已知平面上的三个点
             (xk-1 ,yk-1 ),(xk ,yk ),(xk+1 ,yk+1 ),

求一个二次抛物线, 使得该抛物线经过这三点。
    1.插值基本多项式
有三个插值结点xk-1 ,xk ,xk+1 构造三个插值基本多项式，要求满足：

(1) 基本多项式为二次多项式； (2) 它们的函数值满足下表： 
               
因为lk-1 (xk )= 0,lk-1 (xk+1 )=0, 故有因子(x-xk )(x-xk+1 ), 而其已经是一个二次多项式, 仅相差一个常数倍, 可设
              lk-1 (x)=a(x-xk )(x-xk+1 ),
又因为
               lk-1 (xk-1 )=1 ==> a(xk-1 -xk )(xk-1 -xk+1 )=1
得 
　             　　 

从而

同理得

基本二次多项式见右上图(点击按钮“显示Li”)。

    2. 拉格朗日型二次插值多项式
由前述, 拉格朗日型二次插值多项式:
                P2 (x)=yk-1 lk-1 (x)+yk lk (x)+yk+1 lk+1 (x),P2 (x)
是三个二次插值多项式的线性组合,因而其是次数不超过二次的多项式,且满足:
                P2 (xi )=yi , (i=k-1,k,k+1) 。
例2 已知：
                xi         10      15             20

                yi=lgxi    1    1.1761         1.3010

利用此三值的二次插值多项式求lg12的近似值。
解：设x0 =10,x1 =15,x2 =20,则: 
      
故:
      
      

所以

      
7利用三个点进行抛物插值得到lg12的值,与精确值lg12=1.0792相比,具有3位有效数字,精度提高了。

    三、拉格朗日型n次插值多项式
已知函数y=f(x)在n+1个不同的点x0 ,x1 ,…,x2 上的函数值分别为

y0 ,y1 ,…,yn ,求一个次数不超过n的多项式Pn (x),使其满足:

         Pn (xi )=yi , (i=0,1,…,n),

即n+1个不同的点可以唯一决定一个n次多项式。
    1. 插值基函数
过n+1个不同的点分别决定n+1个n次插值基函数
          l0 (x),l1 (x),…,ln (X)
每个插值基本多项式li (x)满足：

   (1) li (x)是n次多项式;

   (2) li (xi )=1,而在其它n个li (xk )=0 ,(k≠i)。

由于li (xk )=0 ,(k≠i), 故有因子: 

         (x-x0 )…(x-xi-1 )(x-xi+1 )…(x-xn )

因其已经是n次多项式，故而仅相差一个常数因子。令:
          li (x)=a(x-x0 )…(x-xi-1 )(x-xi+1 )…(x-xn )

由li (xi )=1,可以定出a, 进而得到： 

          

2.n次拉格朗日型插值多项式Pn (x)

Pn (x)是n+1个n次插值基本多项式l0 (x),l1 (x),…,ln (X)的线性组合,相应的组合系数是y0 ,y1 ,…,yn。即:

          Pn (x)=y0 l0 (x)+y1 l1 (x)+…+yn ln (x),

从而Pn (x)是一个次数不超过n的多项式,且满足

          Pn (xi )=yi , (i=0,1,2,…,n).

    例3 求过点(2,0),(4,3),(6,5),(8,4),(10,1)的拉格朗日型插值多项式。
解 用4次插值多项式对5个点插值。
                 

   
所以
           

    四、拉格朗日插值多项式的截断误差
我们在[a,b]上用多项式Pn (x) 来近似代替函数f(x), 其截断误差记作 
      Rn (x)=f(x)-Pn (x)
当x在插值结点xi 上时Rn (xi )=f(xi )-P n(xi )=0,下面来估计截断误差：

定理1：设函数y=f(x)的n阶导数y(n) =f(n) (x)在[a,b]上连续，
     y(n+1) = f(n+1) (x)
在(a,b)上存在；插值结点为:
    a≤x0 <x1 <…<xn ≤b,
Pn (x)是n次拉格朗日插值多项式；则对任意x∈[a,b]有： 
       
其中ξ∈(a,b), ξ依赖于x：ωn+1 (x)=(x-x0 )(x-x1 )…(x-xn )

证明：由插值多项式的要求：
      Rn(xi )=f(xi )-Pn (xi )=0，(i=0,1,2,…,n);
设
      Rn (x)=K(x)(x-x0 )(x-x1 )…(x-xn )=K(x)ωn+1 (x)

其中K(x)是待定系数；固定x∈[a,b]且x≠xk ，k=0,1,2,…,n;作函数

       H(t)=f(t)-Pn (t)-K(x)(t-x0 )(t-x1 )…(t-xn )

则 H(xk )=0，(k=0,1,2,…,n), 且H(x)=f(x)-Pn (x)-Rn(x)=0, 所以，

H(t)在[a,b]上有n+2个零点，反复使用罗尔中值定理:存在ξ∈(a,b),


使; 因Pn (x)是n次多项式，故P(n+1) (ξ)=0, 而 

       ωn+1 (t)=(t-x0 )(t-x1 )…(t-xn )

是首项系数为1的n+1次多项式，故有

        
于是
        H(n+1) (ξ)=f(n+1)(ξ)-(n+1)!K(x)
得：
        
所以
        

设 , 则：

        
易知，线性插值的截断误差为:
        
二次插值的截断误差为:
        
下面来分析前面两个例子(例1，例2)中计算lg12的截断误差：
在例1中，用lg10和lg20计算lg12,
       P1(12)=1.0602,lg12=1.0792

       e=|1.0792-1.0602|=0.0190;
估计误差：f(x)=lgx, 
       ,当x∈[10,20]时, 
       

在例2中，用lg10,lg15和lg20计算lg12.
        P2(12)=1.0766,

      e = |1.0792-1.0766|=0.0026
估计误差：