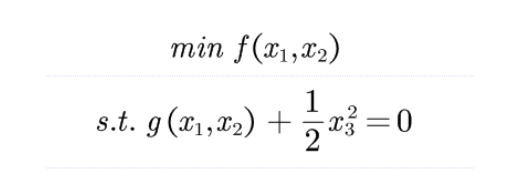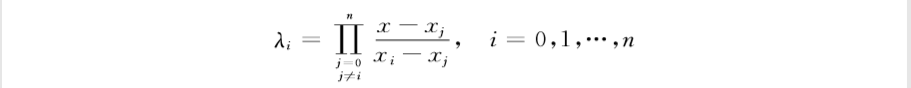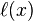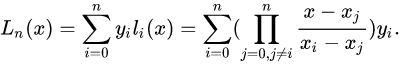0 简单情况
先从简单的情况开始推导,考虑三个向量 a ⃗ , b ⃗ , c ⃗ \vec{a},\vec{b},\vec{c} a,b,c在同一个平面,其中 c ⃗ ⊥ a ⃗ \vec{c} \perp \vec{a} c⊥a,如下图所示,求取 ( a ⃗ × b ⃗ ) × c ⃗ (\vec{a} \times \vec{b}) \times \vec{c} (a×b)×c:
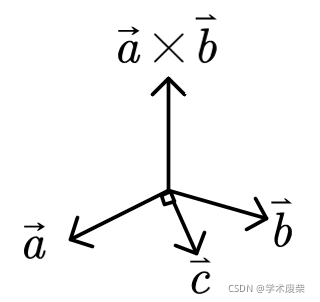
易得 ( a ⃗ × b ⃗ ) × c ⃗ (\vec{a} \times \vec{b}) \times \vec{c} (a×b)×c与 a ⃗ \vec{a} a反向,我们设:
( a ⃗ × b ⃗ ) × c ⃗ = k ⋅ a ⃗ (1) (\vec{a} \times \vec{b}) \times \vec{c}=k \cdot \vec{a} \tag{1} (a×b)×c=k⋅a(1)
其中 k k k为常数,利用长度的性质:
∣ a ⃗ ∣ ∣ b ⃗ ∣ ∣ c ⃗ ∣ s i n ( < a , b > ) = ∣ k ∣ ∣ a ⃗ ∣ (2) |\vec{a}||\vec{b}||\vec{c}|sin(<a,b>)=|k||\vec{a}| \tag{2} ∣a∣∣b∣∣c∣sin(<a,b>)=∣k∣∣a∣(2)
其中 < a , b > <a,b> <a,b>表示向量 a ⃗ , b ⃗ \vec{a},\vec{b} a,b的夹角,根据几何关系可以得到:
∣ b ⃗ ∣ ∣ c ⃗ ∣ s i n ( π 2 ± < b , c > ) = ∣ k ∣ (3) |\vec{b}||\vec{c}|sin(\frac{\pi}{2} \pm <b,c>)=|k|\tag{3} ∣b∣∣c∣sin(2π±<b,c>)=∣k∣(3)
进而:
∣ k ∣ = ∣ b ⃗ ∣ ∣ c ⃗ ∣ c o s ( < b , c > ) = b ⃗ ⋅ c ⃗ (4) |k|=|\vec{b}||\vec{c}|cos(<b,c>)=\vec{b} \cdot \vec{c}\tag{4} ∣k∣=∣b∣∣c∣cos(<b,c>)=b⋅c(4)
得出结论此时,根据几何关系可得正负号:
( a ⃗ × b ⃗ ) × c ⃗ = − ( b ⃗ ⋅ c ⃗ ) ⋅ a ⃗ (5) (\vec{a} \times \vec{b}) \times \vec{c}=-(\vec{b} \cdot \vec{c}) \cdot \vec{a}\tag{5} (a×b)×c=−(b⋅c)⋅a(5)
同理假设 c ⃗ ⊥ b ⃗ \vec{c} \perp \vec{b} c⊥b,此时结果向量与 b ⃗ \vec{b} b同向,可以得出结论:
( a ⃗ × b ⃗ ) × c ⃗ = ( a ⃗ ⋅ c ⃗ ) ⋅ b ⃗ (6) (\vec{a} \times \vec{b}) \times \vec{c}=(\vec{a} \cdot \vec{c}) \cdot \vec{b}\tag{6} (a×b)×c=(a⋅c)⋅b(6)
1 由简单情况到一般情况.
对于任意三维空间向量 c ⃗ \vec{c} c可以分解为垂直 a ⃗ , b ⃗ \vec{a},\vec{b} a,b所在平面的分量 c ⃗ a b \vec{c}_{ab} cab,与 a ⃗ \vec{a} a垂直的分量 c ⃗ a \vec{c}_{a} ca,与 b ⃗ \vec{b} b垂直的分量 c ⃗ b \vec{c}_{b} cb:
( a ⃗ × b ⃗ ) × c ⃗ = ( a ⃗ × b ⃗ ) × ( c ⃗ a + c ⃗ b + c ⃗ a b ) (7) (\vec{a} \times \vec{b}) \times \vec{c}=(\vec{a} \times \vec{b}) \times (\vec{c}_{a}+\vec{c}_{b}+\vec{c}_{ab})\tag{7} (a×b)×c=(a×b)×(ca+cb+cab)(7)
于是根据式(5)(6)以及垂直关系:
( a ⃗ × b ⃗ ) × c ⃗ = ( a ⃗ ⋅ c b ⃗ ) ⋅ b ⃗ − ( b ⃗ ⋅ c a ⃗ ) ⋅ a ⃗ = ( a ⃗ ⋅ c ⃗ ) ⋅ b ⃗ − ( b ⃗ ⋅ c ⃗ ) ⋅ a ⃗ (8) (\vec{a} \times \vec{b}) \times \vec{c}=(\vec{a} \cdot \vec{c_b}) \cdot \vec{b}-(\vec{b} \cdot \vec{c_a}) \cdot \vec{a}=(\vec{a} \cdot \vec{c}) \cdot \vec{b}-(\vec{b} \cdot \vec{c}) \cdot \vec{a}\tag{8} (a×b)×c=(a⋅cb)⋅b−(b⋅ca)⋅a=(a⋅c)⋅b−(b⋅c)⋅a(8)
2 三个三维矢量连续叉乘的矩阵公式
2.1 叉乘的矩阵表示
后文将不再涉及未知数,字母将直接表示矢量。对于一个矢量 w w w其叉乘任意矢量 v v v,等价于一个矩阵乘 v v v,该矩阵记为 w × w_{\times} w×,其值如下:
w × v = w × v = [ 0 − w z w y w z 0 − w x − w y w x 0 ] v (9) w \times v=w_{\times}v=\begin{bmatrix} 0 & -w_z & w_y \\ w_z & 0 & -w_x \\ -w_y & w_x & 0 \end{bmatrix}v\tag{9} w×v=w×v=⎣⎡0wz−wy−wz0wxwy−wx0⎦⎤v(9)
该矩阵的性质如下图,本文只针对连续叉乘的性质(下图性质(7)(8))进行证明,其余的性质比较简单:

先看倒数第二条性质(8),根据式8:
( a × b ) × c = b a T c − a b T c = ( b a T − a b T ) c (10) (a \times b) \times c=ba^Tc-ab^Tc=(ba^T-ab^T)c\tag{10} (a×b)×c=baTc−abTc=(baT−abT)c(10)
从而得:
( a × b ) × = b a T − a b T (11) (a\times b)_{\times}=ba^T-ab^T\tag{11} (a×b)×=baT−abT(11)
性质(9)很容易验证,那么结合性质(8)可以轻易推出性质(7)