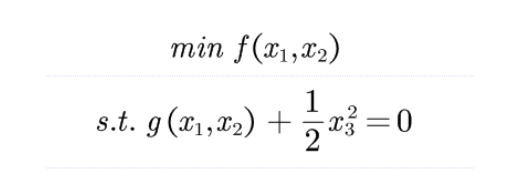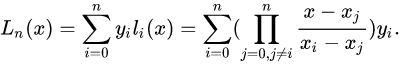一、问题

二、拉格朗日乘数法的基本思想

作为一种优化算法，拉格朗日乘子法主要用于解决约束优化问题，它的基本思想就是通过引入拉格朗日乘子来将含有n个变量和k个约束条件的约束优化问题转化为含有（n+k）个变量的无约束优化问题。拉格朗日乘子背后的数学意义是其为约束方程梯度线性组合中每个向量的系数。

如何将一个含有n个变量和k个约束条件的约束优化问题转化为含有（n+k）个变量的无约束优化问题？拉格朗日乘数法从数学意义入手，通过引入拉格朗日乘子建立极值条件，对n个变量分别求偏导对应了n个方程，然后加上k个约束条件（对应k个拉格朗日乘子）一起构成包含了（n+k）变量的（n+k）个方程的方程组问题，这样就能根据求方程组的方法对其进行求解。

三、拉格朗日手工求解

三、拉格朗日 python 求解

代码如下

# 导入包
from sympy import *
# 设置变量
x,y,z,k = symbols('x,y,z,k')
a,b,c=symbols('a,b,c')
f = 8*x*y*z
g = x**2/a**2+y**2/b**2+z**2/c**2-1
#构造拉格朗日函数
L=f+k*g
#求导
dx = diff(L, x)   # 对x求偏导
print("dx=",dx)
dy = diff(L,y)   #对y求偏导
print("dy=",dy)
dz = diff(L,z)   #对z求偏导
print("dz=",dz)
dk = diff(L,k)   #对k求偏导
print("dk=",dk)
dx= 8*y*z + 2*k*x/a**2
dy= 8*x*z + 2*k*y/b**2
dz= 8*x*y + 2*k*z/c**2
dk= -1 + z**2/c**2 + y**2/b**2 + x**2/a**2
#求出个变量解
m= solve([dx,dy,dz,dk],[x,y,z,k])   
print(m)
#变量赋值
x=sqrt(3)*a/3
y=sqrt(3)*b/3
z=sqrt(3)*c/3
k=-4*sqrt(3)*a*b*c/3
#计算方程的值
f = 8*x*y*z
print("方程的最大值为：",f)

四、小结

感觉使用python求解某些数学问题非常的方便

五、参考资料

1.使用拉格朗日方法分别手工求解、python编程求解条件极值问题