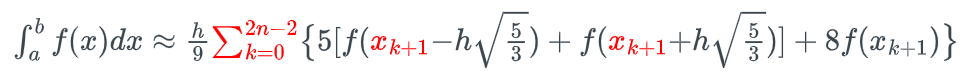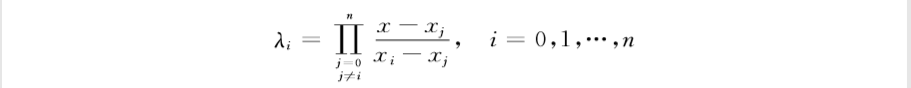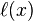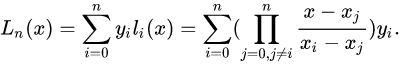众所周知，Logx精通Excel。
他觉得表格只有单调的白色非常无聊，他决定将一些单元格涂黑。

在一个n行m列的表格里，刚开始所有单元格都是白的。
Logx打算在这个表格选出三个不同的单元格A(x1,y1),B(x2,y2),C(x3,y3)，并将选中的三个单元格涂黑。
为了使表格看起来美观，Logx会使每一行和每一列均至多有一个格子被涂黑。
他称一种选择方案是好的，当且仅当L≤|x1-x2|+|y1-y2|+|x2-x3|+|y2-y3|+|x1-x3|+|y1-y3|≤R，即这三个黑格子之间两两的曼哈顿距离之和在区间[L,R]内。其中L,R是他给定的两个常数。
两种方案不同，当且仅当存在一个格子，在一种方案中被涂黑了，在另一种方案中没有被涂黑。
Logx想要知道，有多少种选择方案是好的。
 

输入

输入仅一行，包含四个正整数 n,m,L,R，含义见题目描述。

输出

输出一行一个整数表示方案数。
由于答案可能很大，你只要输出方案数对10^9+7取模的结果。

 

样例输入 Copy

【样例1】
3 3 1 20000
【样例2】
3 3 4 7
【样例3】
4 6 9 12
【样例4】
7 5 13 18
【样例5】
4000 4000 4000 14000

样例输出 Copy

【样例1】
6
【样例2】
0
【样例3】
264
【样例4】
1212
【样例5】
859690013

提示

对于所有数据，3≤n,m≤10^16,1≤L≤R≤10^18。

 

结论：

1. 设三个不在同行同列的黑格子所围成的长方形为x * y，那么三个黑格子两两之间距离和为2 * (x + y - 2);

2. 设三个不在同行同列的黑格子所围成的长方形为x * y，有6 * (x - 2) * (y - 2)种方法放置三个黑格子;

3. 一个大小为x * y的长方形在n * m的格子中有(n - x + 1) * (m - y + 1);

 

首先将(L, R)区间拆成(1,R) - (1, L - 1)

所以

 

 

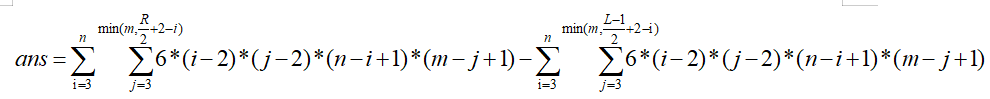
H1（x）用拉格朗日插值法算出来

H2(x)可以直接用公式或者同第一步用拉格朗日插值

最暴力的代码O(n*m)

/**/
#pragma GCC optimize(3,"Ofast","inline")
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cctype>
#include <iostream>
#include <algorithm>
#include <map>
#include <set>
#include <vector>
#include <string>
#include <stack>
#include <queue>typedef long long LL;
using namespace std;const long long mod = 1e9 + 7;LL n, m, l, r;
LL pw6, pw2;LL poww(LL x, LL num){LL res = 1;while(num){if(num & 1) res = res * x % mod;x = x * x % mod;num >>= 1;}return res;
}LL cal(LL x, LL y){return (x - 2) * (y - 2) % mod * 6 % mod;
}LL cal1(LL x){return x * (x + 1) % mod * (2 * x + 1) % mod * pw6 % mod;
}int main()
{//freopen("in.txt", "r", stdin);//freopen("out.txt", "w", stdout);pw6 = poww(6, mod - 2);pw2 = poww(2, mod - 2);scanf("%lld %lld %lld %lld", &n, &m, &l, &r);LL ans = 0;for (LL i = 3; i <= min(r / 2 - 1, n); i++){LL L = max(3LL, (l + 1) / 2 + 2 - i), R = min(2 - i + r / 2, m);for (LL j = L; j <= R; j++){ans += cal(i % mod, j % mod) * ((n - i + 1) % mod) % mod * ((m - j + 1) % mod) % mod;ans %= mod;}}printf("%lld\n", ans);return 0;
}
/**/

暴力代码(n)

/**/
#pragma GCC optimize(3,"Ofast","inline")
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cctype>
#include <iostream>
#include <algorithm>
#include <map>
#include <set>
#include <vector>
#include <string>
#include <stack>
#include <queue>typedef long long LL;
using namespace std;const long long mod = 1e9 + 7;LL n, m, l, r;
LL pw6, pw2;LL poww(LL x, LL num){LL res = 1;while(num){if(num & 1) res = res * x % mod;x = x * x % mod;num >>= 1;}return res;
}LL cal(LL x, LL y){return (x - 2) * (y - 2) % mod * 6 % mod;
}LL cal1(LL x){return x * (x + 1) % mod * (2 * x + 1) % mod * pw6 % mod;
}int main()
{//freopen("in.txt", "r", stdin);//freopen("out.txt", "w", stdout);pw6 = poww(6, mod - 2);pw2 = poww(2, mod - 2);scanf("%lld %lld %lld %lld", &n, &m, &l, &r);LL ans = 0;for (LL i = 3; i <= min(r / 2 - 1, n); i++){LL L = max(3LL, (l + 1) / 2 + 2 - i), R = min(2 - i + r / 2, m);LL t1 = (cal1((L - 1) % mod) - cal1(R % mod)) % mod;LL t2 = (m + 3) % mod * ((R - L + 1) % mod) % mod * ((R + L) % mod) % mod * pw2 % mod;LL t3 = 2 * (m + 1) % mod * ((R - L + 1) % mod) % mod;LL t = ((t1 + t2 - t3) % mod + mod) % mod;ans = (ans + t * 6 % mod * ((i - 2) % mod) % mod * ((n - i + 1) % mod) % mod) % mod;}printf("%lld\n", ans);return 0;
}
/**/

AC代码:

/**/
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cctype>
#include <iostream>
#include <algorithm>
#include <map>
#include <set>
#include <vector>
#include <string>
#include <stack>
#include <queue>typedef long long LL;
using namespace std;const int D = 1e3 + 10;const long long mod = 1e9 + 7;LL n, m, l, r, R, pw2, pw6;
LL a[D], f[D], g[D], p[D], p1[D], p2[D], b[D], h[D][2], C[D];LL poww(LL x, LL num){LL res = 1;while(num){if(num & 1) res = res * x % mod;x = x * x % mod;num >>= 1;}return res;
}void init(int M){f[0] = f[1] = g[0] = g[1] = 1;for (int i = 2; i <= M + 4; i++) f[i] = f[i - 1] * i % mod;g[M + 4] = poww(f[M + 4], mod - 2);for (int i = M + 3; i >= 1; i--) g[i] = g[i + 1] * (i + 1) % mod;
}LL sum(LL x, LL y){return ((x - 2) % mod) * ((y - x + 1) % mod) % mod;
}LL calcn(int d, LL *a, LL n){// a[0].. a[d]  a[n]if(n <= d) return a[n];p1[0] = p2[0] = 1;for (int i = 0; i <= d; i++){LL t = (n - i + mod) % mod;p1[i + 1] = p1[i] * t % mod;}for (int i = 0; i <= d; i++){LL t = (n - d + i + mod) % mod;p2[i + 1] = p2[i] * t % mod;}LL ans = 0;for (int i = 0; i <= d; i++){LL t = g[i] * g[d - i] % mod * p1[i] % mod * p2[d - i] % mod * a[i] % mod;if((d - i) & 1) ans = (ans - t + mod) % mod;else ans = (ans + t) % mod;}return ans;
}LL polysum(LL m, LL *a, LL n){// a[0].. a[m] \sum_{i=0}^{n} a[i]if(n <= m){LL sum = 0;for (int i = 0; i <= n; i++) sum = (sum + a[i]) % mod;return sum;}LL b[D];for (int i = 0; i <= m; i++) b[i] = a[i];b[m + 1] = calcn(m, b, m + 1);for (int i = 1; i <= m + 1; i++) b[i] = (b[i - 1] + b[i]) % mod;return calcn(m + 1, b, n);// m次多项式的和是m+1 次多项式
}LL cal3(LL x){return x * (x + 1) % mod * (2 * x + 1) % mod * pw6 % mod;
}LL solve(LL L, LL R){if(L > R) return 0LL;LL t1 = (cal3((L - 1) % mod) - cal3(R % mod)) % mod;LL t2 = (m + 3) % mod * ((R - L + 1) % mod) % mod * ((R + L) % mod) % mod * pw2 % mod;LL t3 = 2 * (m + 1) % mod * ((R - L + 1) % mod) % mod;LL t = ((t1 + t2 - t3) % mod + mod) % mod;return t;
}LL cal1(LL l, LL r){if(l > r) return 0LL;LL a[15];for (int i = 0; i <= 5; i++) a[i] = sum(l + i, n) * solve(3, R / 2 - l - i + 2) % mod;return polysum(5, a, r - l);
}LL cal2(LL l, LL r){if(l > r) return 0LL;LL a[15];a[0] = 0;for (int i = 0; i <= 2; i++) a[i] = sum(l + i, n) * solve(3, m) % mod;return polysum(2, a, r - l);
}LL cal(LL x){if(!x) return 0LL;LL L1 = x / 2 - m + 2, R1 = min(n, x / 2 - 1);LL L2 = 3, R2 = x / 2 - m + 1;if(R2 < L2) return cal1(max(3LL, L1), R1);else if(R2 >= n) return cal2(L2, min(R2, n));else return cal1(L1, R1) + cal2(L2, R2);
}int main()
{//freopen("in.txt", "r", stdin);//freopen("out.txt", "w", stdout);pw2 = poww(2, mod - 2), pw6 = poww(6, mod - 2);init(1000);scanf("%lld %lld %lld %lld", &n, &m, &l, &r);R = r;LL ans = cal(r);R = l - 1;ans -= cal(l - 1);printf("%lld\n", (ans + mod) % mod * 6 % mod);return 0;
}
/**/