问题
给定 n n n 个点,可确定一个多项式 y = f ( x ) y=f(x) y=f(x) ,要求确定这个多项式并求出 f ( k ) f(k) f(k)
拉格朗日(Lagrange)插值公式
搬运
令 L n ( x ) = f ( x ) L_n(x)=f(x) Ln(x)=f(x)
n=1
有

由点斜式可以得到

其中

这里 l k ( x ) l_k(x) lk(x) 和 l k + 1 l_{k+1} lk+1 称作线性插值基函数。
n=2
有
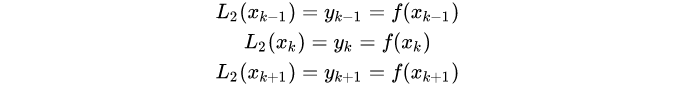
构造
![[公式]](https://img-blog.csdnimg.cn/b0f5a3b9f44b4b45a165df00513b9a42.png)
易得
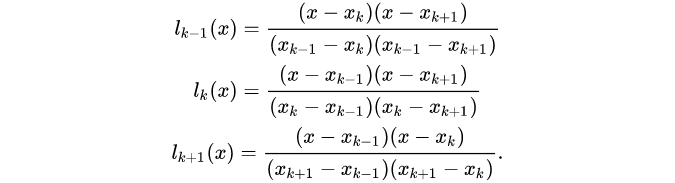
一般情况
L n ( x ) = l 0 ( x ) ∗ y 0 + l 1 ( x ) ∗ y 1 + l 2 ( x ) ∗ y 2 + . . . + l n ( x ) ∗ y n L_n(x)=l_0(x)*y_0+l_1(x)*y_1+l_2(x)*y_2+...+l_n(x)*y_n Ln(x)=l0(x)∗y0+l1(x)∗y1+l2(x)∗y2+...+ln(x)∗yn
其中

于是
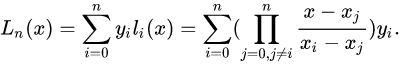
因此,求 f ( k ) f(k) f(k) 直接将 k k k 带入即可
时间复杂度 O ( n 2 ) O(n^2) O(n2)
高斯消元 O ( n 3 ) O(n^3) O(n3) 求系数
代码
#include<bits/stdc++.h>
#define LL long long
#define mod 998244353
using namespace std;
const int N=2e3+9;
int n;
LL k,ans;
LL x[N],y[N];
LL Inv(LL a,LL b)
{LL tot=1LL;while(b){if(b&1) (tot*=a)%=mod;(a*=a)%=mod; b>>=1;}return tot;
}
LL Lagrange()
{for(int i=1;i<=n;i++){LL fz=1LL,fm=1LL;for(int j=1;j<=n;j++)if(i!=j){(fz*=(k-x[j]))%=mod;(fm*=(x[i]-x[j]))%=mod;}(ans+=y[i]*fz%mod*Inv(fm,mod-2)%mod+mod)%=mod;}return ans;
}
int main()
{scanf("%d%lld",&n,&k);for(int i=1;i<=n;i++)scanf("%lld%lld",&x[i],&y[i]);printf("%lld\n",Lagrange());return 0;
}