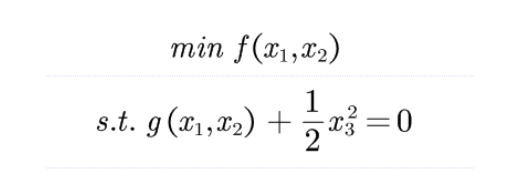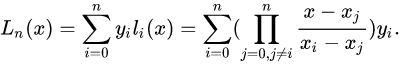1.我们已知SVM损失函数是带有约束条件的损失函数,对于无约束条件的损失函数求最小我们知道可以对x求导等于0求得x等于多少时y最小,但是如果我们给定一个约束条件,那么下相应的结果也会改变。
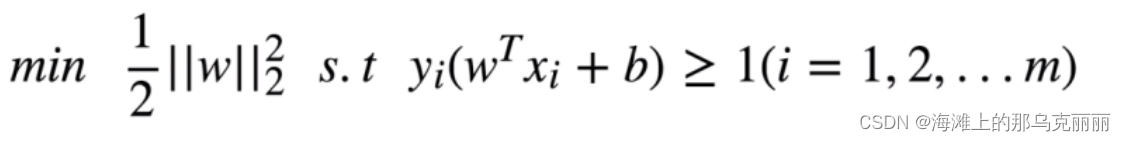
2.对于SVM带有约束条件的损失函数,我们如何求W?
用拉格朗日函数解决带有约束条件的最优化问题。
我们要求一个函数的最优解,求这个函数最小的时候所对应的x是何值,这个函数有带有两个约束条件,,
,只要问题可以写成这种形式(使用拉格朗日函数须满足的形式),那么就可以用拉格朗日函数去解决这样的问题。
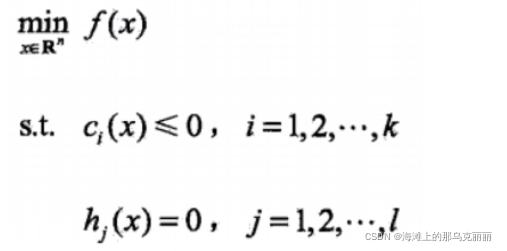
3.因为SVM损失函数是带有约束条件的最优化问题,我们就将SVM写成拉格朗日需要满足的形式
SVM约束条件可以写成,i = 1, 2, 3...m 这个式子符合拉格朗日原始问题里面的
。
前面SVM损失函数没有等式约束条件,所以不用考虑。
4. 拉格朗日函数
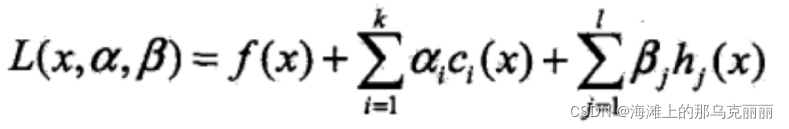
原始问题,
不等式约束条件,
乘子,前面加和:k个不等式约束条件加和
后面是等式约束条件,因为没有等式约束条件,所以不考虑,等于0
拉格朗日函数相当于把有约束条件的最优化问题变成无约束条件的最优化问题。把f(x)和约束条件整合在一起,变成一个式子再进行优化。也就相当于对带有约束条件的原始问题进行优化。
5.拉格朗日函数特性
拉格朗日函数乘子必须大于等于0
如果我们对拉格朗日函数求最大,我们就会得到原始问题f(x)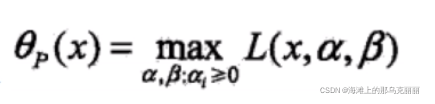
我们对拉格朗日函数求最大,因为>=0,
<=0,所以
,又因为
,所以
乘子部分相乘等于零。
所以对拉格朗日取最大的时候就是时,那么拉格朗日公式就是变成了原始问题f(x)+0=f(x)。
我们在对求最大后的f(x)求最小,就是我们最终要求的二次优化问题。
6.对偶问题
对于,我们可以先求最小再求最大
当f(x)和ci函数是凸函数,hj函数是仿射函数,就可以将min max变成max min
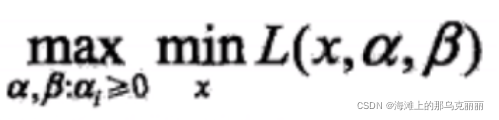
这里的x就是w。
7.KKT条件
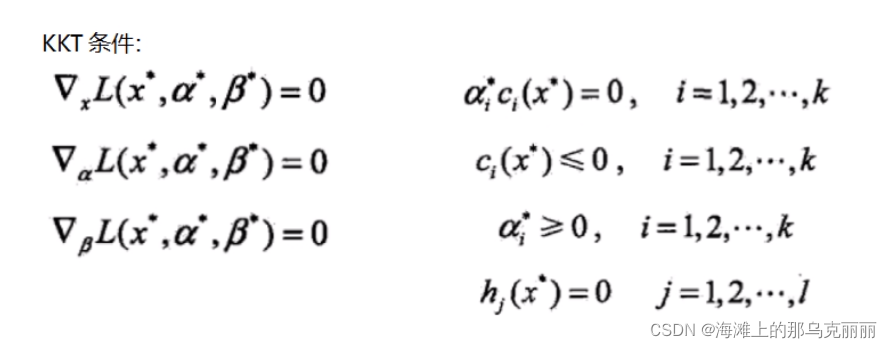
8.把SVM损失函数原始问题转换成拉格朗日函数的形式。再用对偶问题把求解最小最大变成求最大最小。
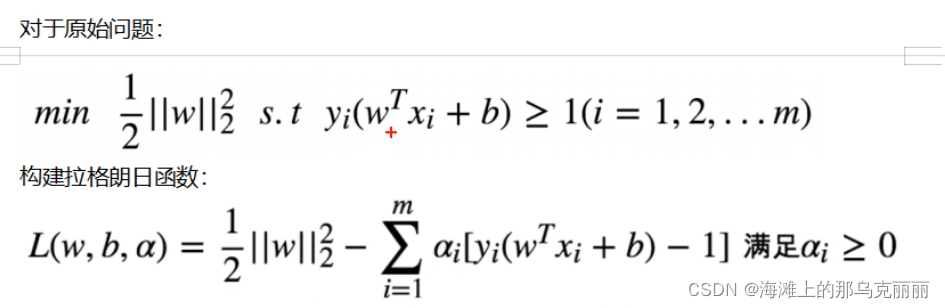
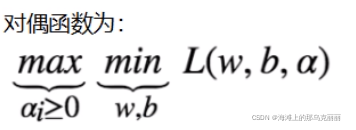

得到两个中间结果,

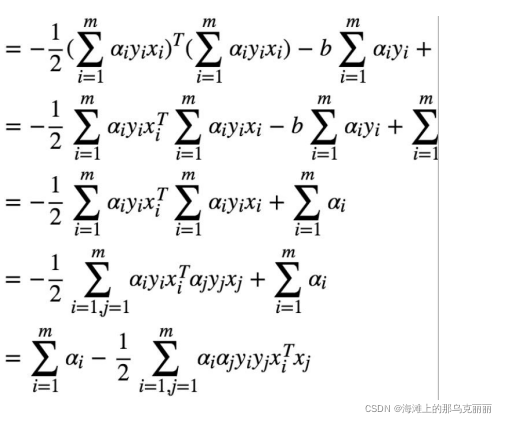
得到结果

通常使用 SMO 算法进行求解,可以求得一组α* 使得函数最优化。
9.得到最终超平面
假设已经通过 SMO 算法,求得α*,此时求 w*很容易:
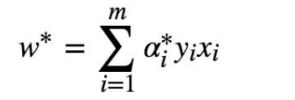
根据KKT条件
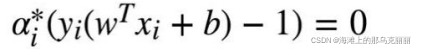
因为a>0,所以要满足以上KKT条件,
所以,由此可以看出a>0时所对应的x,y正是支持向量的x,y
那么通过SMO算法求得的m个a,我们就可以找一下这m个a中有几个>0,对应的x,y
就是支持向量的x,y
又因为支持向量有
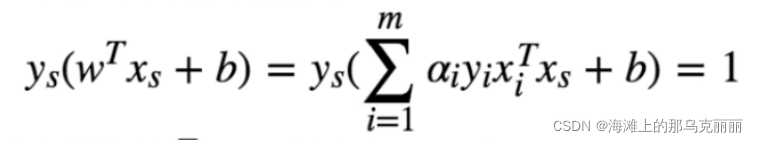
带入求得的支持向量x,y就能求出b的值。
知道W和b之后,我们就能确定好分割超平面

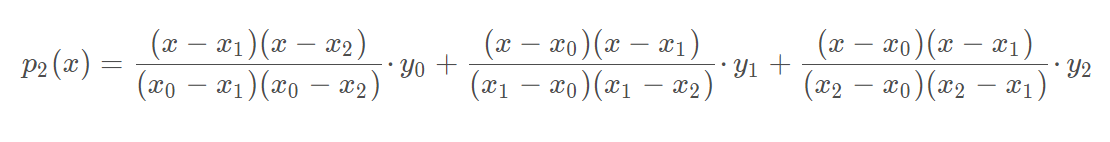



![[计算机数值分析]拉格朗日插值公式](https://img-blog.csdnimg.cn/20210420211706296.png#pic_center)