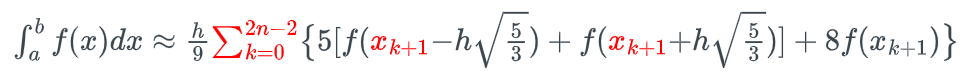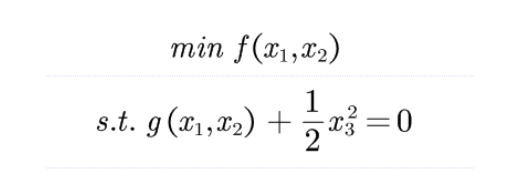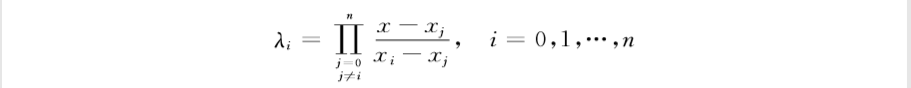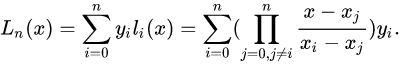泰勒公式
泰勒公式,是一个用函数在某点的信息描述其附近取值的公式。如果函数满足一定的条件,泰勒公式可以用函数在某一点的各阶导数值做系数构建一个多项式来近似表达这个函数。
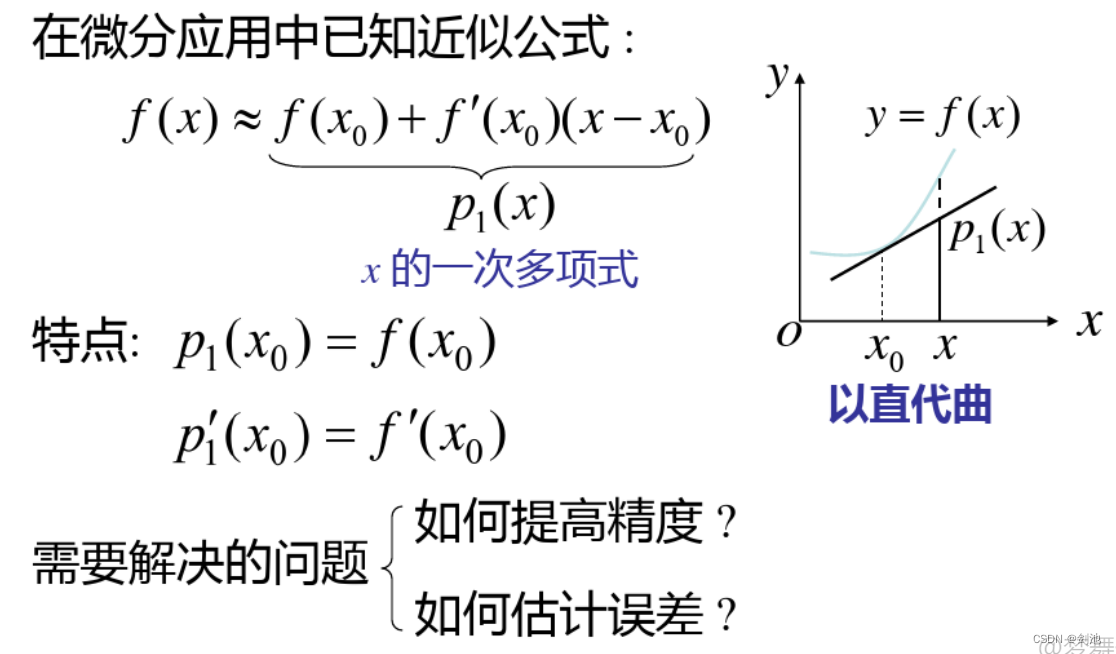
以直代曲
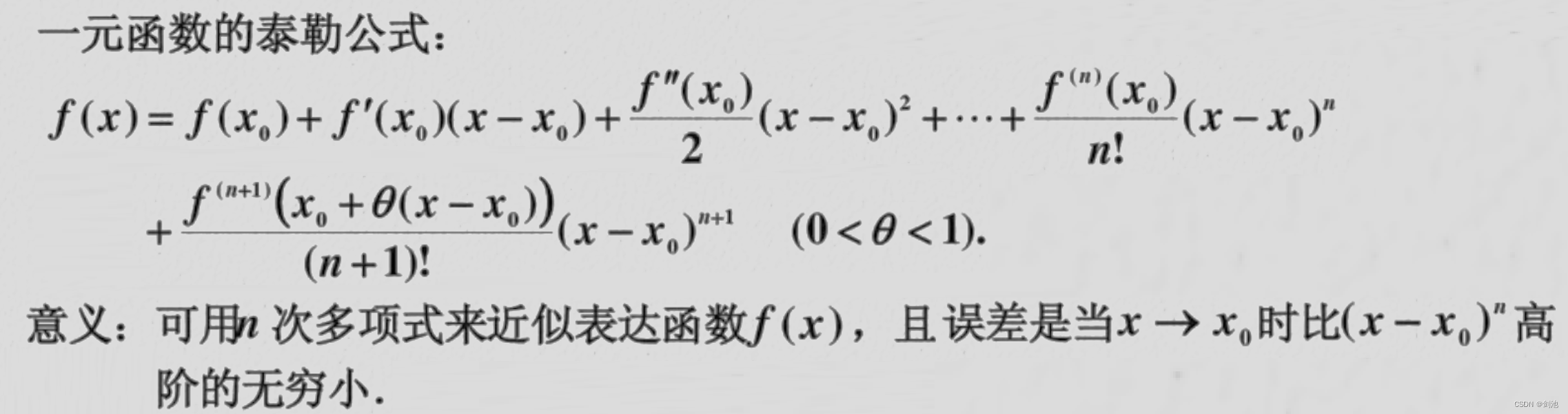
泰勒公式中,如果 ,则是麦克劳林公式:
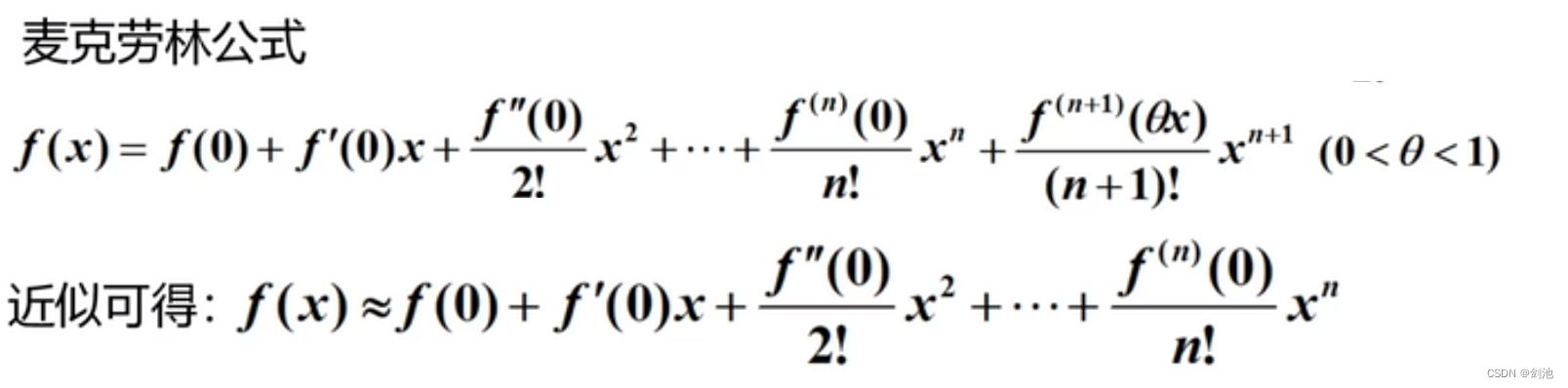
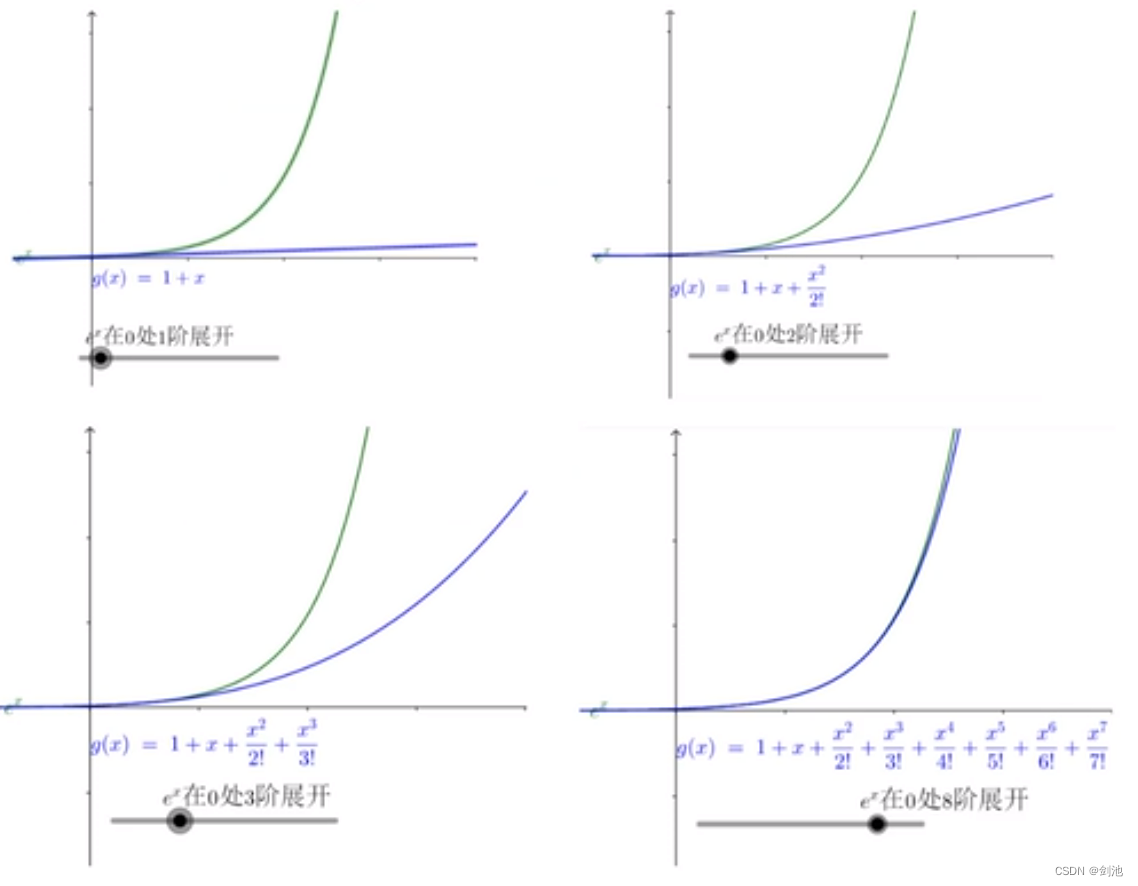
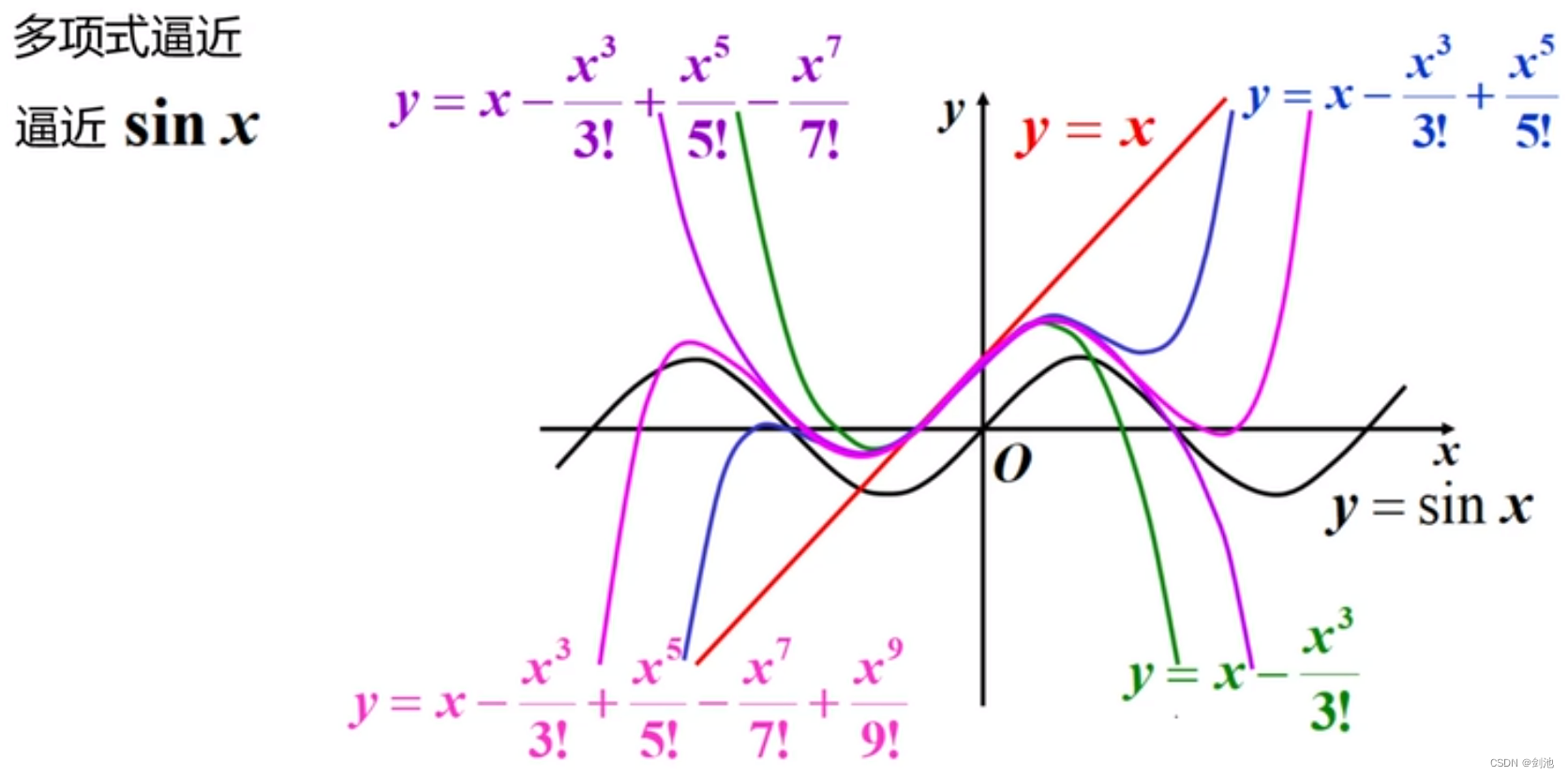
多项式逼近。对于函数 ,在 x = 0 处进行一阶展开,二阶展开,多阶展开

一些常用函数的泰勒公式 :
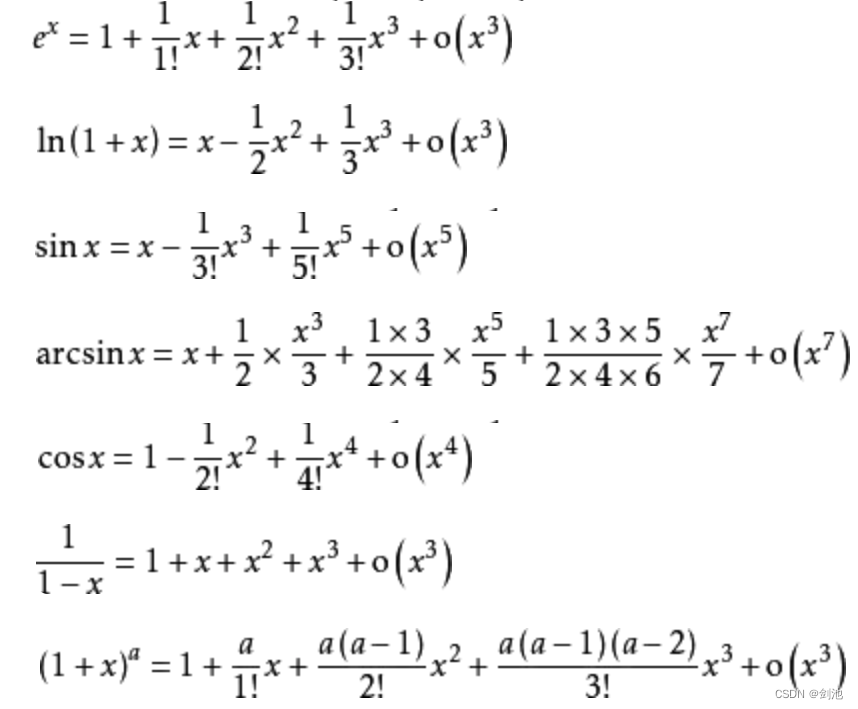
泰勒公式的应用
在近似计算中的应用:



拉格朗日乘子法
是求函数 f(x1,x2,...) 在 g(x1,x2,...)=0 的约束条件下的极值的方法。其主要思想是引入一个新的参数 λ (即拉格朗日乘子),将约束条件函数与原函数联系到一起,使能配成与变量数量相等的等式方程,从而求出得到原函数极值的各个变量的解。



例题:



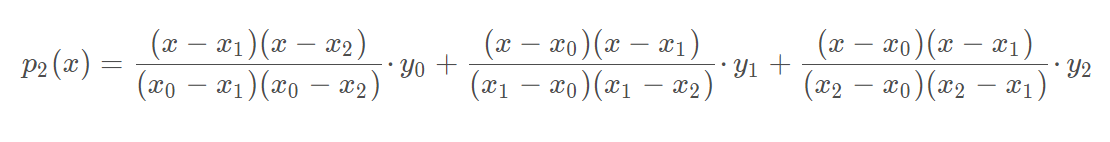



![[计算机数值分析]拉格朗日插值公式](https://img-blog.csdnimg.cn/20210420211706296.png#pic_center)