数据模型的基本概念

模型就是对现实世界特征的模拟和抽象，数据模型是对现实世界数据特征的抽象。对于具体的模型人们并不陌生，如航模飞机、地图和建筑设计沙盘等都是具体的模型。最常用的数据模型分为概念数据模型和基本数据模型。
1）概念数据模型
概念数据模型也称为信息模型，是按用户的观点对数据和信息建模，是现实世界到信息世界的第一层抽象，强调其语义表达功能，易于用户理解，是用户和数据库设计人员交流的语言，
主要用于数据库设计。这类模型中最著名的是实体联系模型，简称 E-R 模型。
2）基本数据模型
基本数据模型是按计算机系统的观点对数据建模，是现实世界数据特征的抽象，用于DBMS 的实现。不同的数据模型具有不同的数据结构形式，目前最常用的数据结构模型有层次模型（hierarchical model）、网状模型（network model）、关系模型（relational Model）和面向对象数据模型（object oriented model）。
关系数据库系统是采用关系模型作为数据的组织方式，在关系模型中用二维表格结构表达实体集，以及实体集之间的联系，其最大特色是描述的一致性。关系模型是由若干个关系模式组成的集合。一个关系模式相当于一个记录型，对应于程序设计语言中类型定义的概念。关系是一个实例，也是一张表，对应于程序设计语言中的变量的概念。给定变量的值随时间可能发生变化；类似地，当关系被更新时，关系实例的内容也随时间发生了变化。  

 数据模型的三要素
数据库结构的基础是数据模型，是用来描述数据的一组概念和定义。数据模型的三要素是数据结构、数据操作和数据的约束条件。
（1）数据结构：是所研究的对象类型的集合，是对系统静态特性的描述。
（2）数据操作：对数据库中各种对象（型）的实例（值）允许执行的操作的集合，包括操作及操作规则。如操作有检索、插入、删除和修改，操作规则有优先级别等。数据操作是对系统动态特性的描述。
（3）数据的约束条件：是一组完整性规则的集合。也就是说，对于具体的应用数据必须遵循特定的语义约束条件，以保证数据的正确、有效和相容。


.E-R模型
概念模型是对信息世界建模,所以概念模型能够方便、准确地表示信息世界中的常用概念。概念模型有很多种表示方法，其中最为常用的是用 E-R 图来描述现实世界的概念模型，称为实体-联系模型（Entity-Relationship Model，E-R 模型）。E-R 模型是软件工程设计中的一个重要方法，在数据库设计中，常用 E-R 模型来描述现实世界到信息世界的问题。因为它接近于人的思维方式，容易理解并且与计算机无关，所以用户容易接受，是用户和数据库设计人员交流的语言。但是，E-R 模型只能说明实体间的语义联系,还不能进一步地详细说明数据结构。在解决实际应用问题时，通常应该先设计一个 E-R 模型，然后再把其转换成计算机能接受的数据模型。

1.E-R 方法

概念模型中最常用的方法为实体-联系方法，简称 E-R 方法。该方法直接从现实世界中抽象出实体和实体间的联系，然后用非常直观的 E-R 图来表示数据模型。

下图是E-R图的主要构件

在E-R图中，实体集作为主码（或者是主键）的一部分属性名下面加下划线标明，另外在实体集与联系的线段上标注联系的类型。

2.实体

从表中可见，在 E-R 模型中实体用矩形表示，通常矩形框内写明实体名。实体是现实世界中可以区别于其他对象的“事件”或“物体”。例如，企业中的每个人都是一个实体。每个实体由一组特性（属性）来表示，其中的某一部分属性可以唯一标识实体，如职工号。实体集是具有相同属性的实体集合，例如，学校所有教师具有相同的属性，因此教师的集合可以定义为一个实体集；学生具有相同的属性，因此学生的集合可以定义为另一个实体集。

3.联系

在ER 模型中，联系用菱形表示，如表 6-1 所示。通常可在菱形框内写明联系名，并用无向边分别与有关实体连接起来，同时在无向边旁标注上联系的类型（1：1、1：*或*：*）。实体的联系分为实体内部的联系和实体与实体之间的联系。实体内部的联系反映数据在同一记录内部各字段间的联系。

1）两个不同实体之间的联系
两个实体之间的联系可分为 3 类:

一对一联系记为 1：1,

一对多联系记为1：*(或 1：n)，

多对多联系记为*：*（或 m：n）。

(1）1： 1。如果对于实体集 A 中的每一个实体，实体集 B 中至多有一个实体与之对应，反之亦然，则称 A 与 B 具有一对一联系。

(2) 1：*。如果对于实体集 A 中的每一个实体，实体集 B 中有 n个实体（n≥0）与之对应；反之，对于实体集 B 中的每一个实体，实体集 A 中至多只有一个实体与之对应，则称 A与B具有一对多联系。

（3）*：*。如果对于实体集 A 中的每一个实体，实体集 B 中有 n 个实体（n≥0）与之对
应；反之，对于实体集 B 中的每一个实体，实体集 A中也有m个实体（m≥0）与之对应，则称 A 与 B 具有多对多联系。

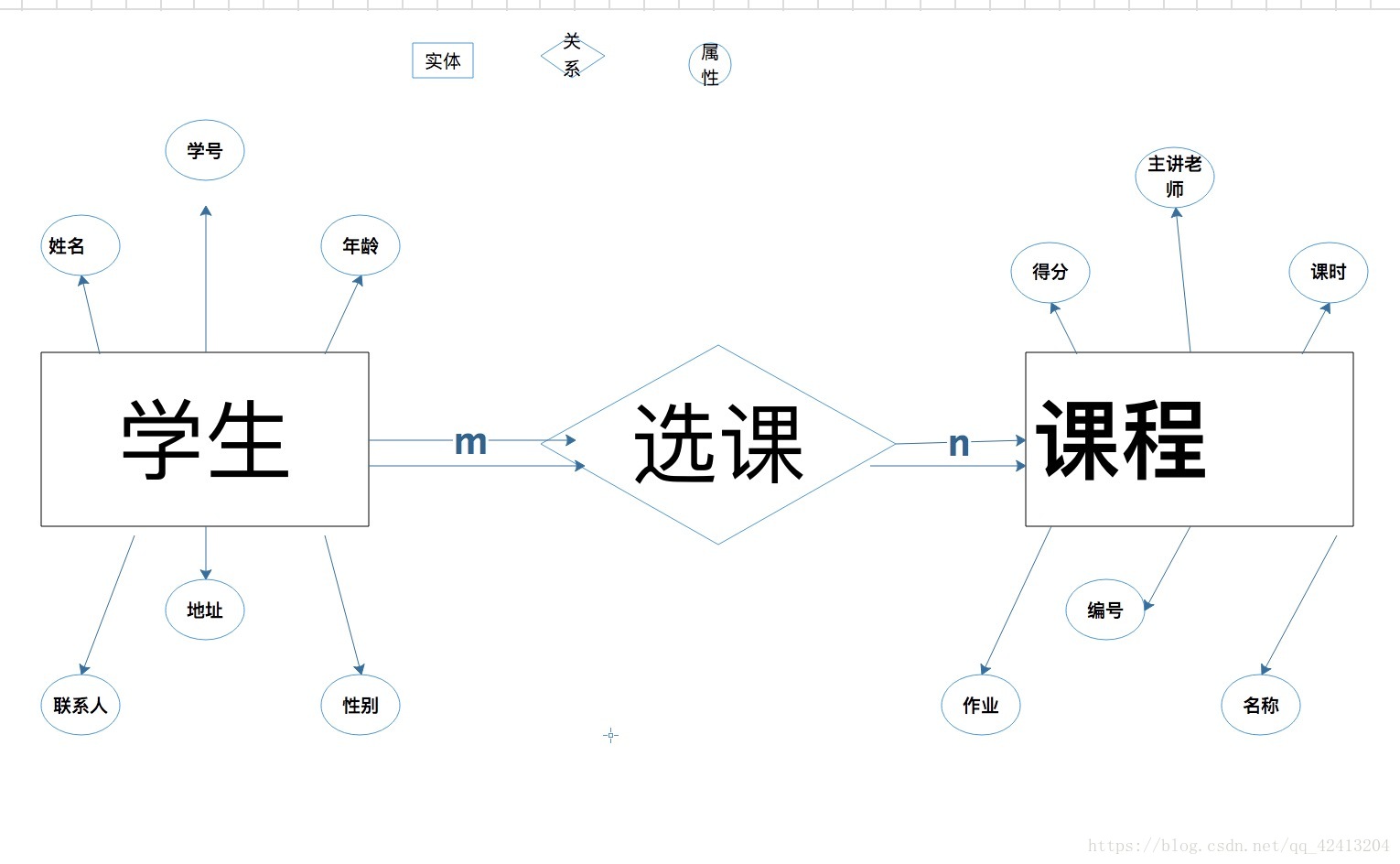
例如下图：

左边图：每个学生只有一个学号，所以是1：1的联系。

中间图：一个班级里面可有多个学生，一个学生只对于一个班级，所以是 1：*的联系。

右边图：一个学生可以有多个老师，一个老师也可以教多个学生，所以是 *：*的联系。

2）两个以上不同实体集之间的联系。

 一个学校中有多个学生，也有多个老师，而一个学生只在一个学校，一个老师也只在一个学校。

3）同一实体集内的二元联系

 职工实体集中的领导与被领导联系是1：* 

职工实体集中的婚姻联系是1：1  

4.属性

属性是实体某方面的特性。例如，职工实体集具有职工号、姓名、年龄、参加工作时间和通信地址等属性。每个属性都有其取值范围，在同一实体集中，每个实体的属性及其域是相同的，但可能取不同的值。E-R 模型中的属性有如下分类：
（1）简单属性和复合属性。简单属性是原子的、不可再分的，复合属性可以细分为更小的部分（即划分为别的属性）。有时用户希望访问整个属性，有时希望访问属性的某个成分，那么在模式设计时可采用复合属性。例如，职工实体集的通信地址可以进一步分为邮编、省、市、街道。若不特别声明，通常指的是简单属性。
（2）单值属性和多值属性。前面所举的例子中，定义的属性对于一个特定的实体都只有单独的一个值。例如，对于一个特定的职工，只对应一个职工号、职工姓名，这样的属性叫作单值属性。但是，在某些特定情况下，一个属性可能对应一组值。例如，职工可能有 0 个、1 个或多个亲属，那么职工的亲属的姓名可能有多个数目，这样的属性称为多值属性。
（3）NULL 属性。当实体在某个属性上没有值或属性值未知时，使用 NULL 值。表示无意义或不知道。
（4）派生属性。派生属性可以从其他属性得来。例如，职工实体集中有“参加工作时间”和“工作年限”属性，那么“工作年限”的值可以由当前时间和参加工作时间得到。这里，“工作年限”就是一个派生属性。


 5.扩充的E-R模型

1）弱实体

在现实世界中有一种特殊的依赖联系，该联系是指某实体是否存在对另一些实体具有很强的依赖关系，即一个实体的存在必须以另一个实体为前提。而将这类实体称为弱实体，例如学生和学生家属，家属是属于学生的，若学生不属于这个学校那么学生家属也将从关系中删除，所用家属就是弱实体。

2）特殊化
前面已经介绍了，实体集是具有相同属性的实体集合。但在现实世界中，某些实体一方面具有一些共性，另一方面还具有各自的特殊性。这样，一个实体集可以按照某些特征区分为几个子实体。
设有实体集E，如果S 是E的某些真子集的集合，记为S={Si|Si∈E,i=1,2,3…,n}时，则称 S是E的一个特殊化，E是S1,S2.…… Sn，的超类，S1,S2.…… Sn称为E的子类。
如果Ui=1-n   Si=E，则称 S 是E的全特殊化，否则是E 的部分特殊化。
如果Si和Sj的交集是空集，i不等于j，则 S 是不相交特殊化，否则是重叠特殊化。
在扩充的 E-R 模型中，子类继承超类的所有属性和联系，但是，子类还有自己特殊的属性和联系。超类-子类关系模型使用特殊化圆圈和连线的一般方式来表示。超类到圆圈有一条连线，连线为双线表示全特殊化，连线为单线表示部分特殊化；双竖边矩形框表示子类；有符号“U”的线表示特殊化；圆圈中的d表示不相交特殊化；圆圈中的 o表示重叠特殊化。

扩充 E-R 图中的主要构件