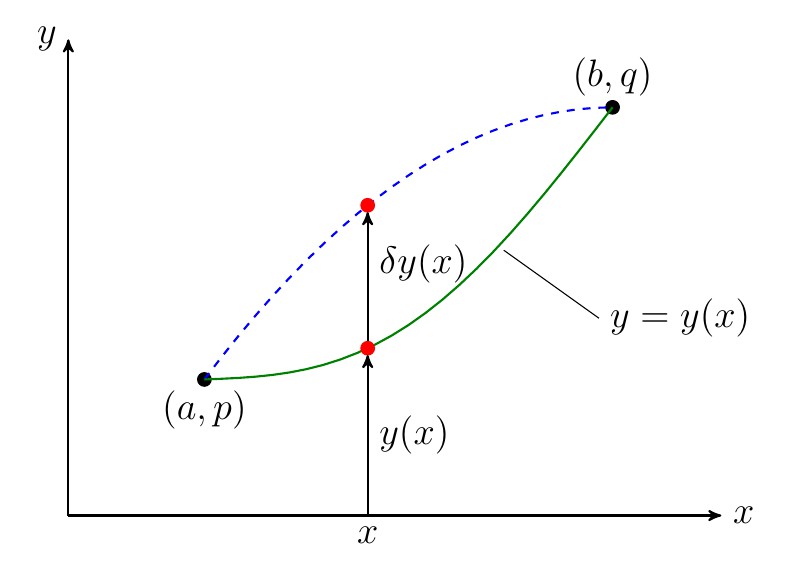
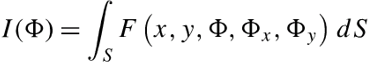AbstractQueuedSynchronizer
简写为AQS,抽象队列同步器。它是一个用于构建锁和同步器的框架,许多同步器都可以通过AQS很容易并且高效的构造出来,以下都是通过AQS构造出来的:ReentrantLock, ReentrantReadWriteLock
AQS使用了模板方法,把同步队列都封装起来了,同时提供了以下五个未实现的方法,用于子类的重写:
- boolean tryAcquire(int arg):尝试以独占模式进行获取。
此方法应查询对象的状态是否允许以独占模式获取对象,如果允许则获取它。如果获取失败,则将当前线程加入到等待队列,直到其他线程唤醒。 - boolean tryRelease(int arg):尝试以独占模式释放锁。
- int tryAcquireShared(int
arg):尝试以共享模式获取锁,此方法应查询对象的状态是否允许以共享模式获取对象,如果允许则获取它。如果获取失败,则将当期线程加入到等待队列,直到其他线程唤醒。 - boolean tryReleaseShared(int arg):尝试以共享模式释放锁。
- boolean isHeldExclusively():是否独占模式

- state:所有线程通过通过CAS尝试给state设值,当state>0时表示被线程占用;同一个线程多次获取state,会叠加state的值,从而实现了可重入;
- exclusiveOwnerThread:在独占模式下该属性会用到,当线程尝试以独占模式成功给state设值,该线程会把自己设置到exclusiveOwnerThread变量中,表明当前的state被当前线程独占了;
- 等待队列(同步队列):等待队列中存放了所有争夺state失败的线程,是一个双向链表结构。state被某一个线程占用之后,其他线程会进入等待队列;一旦state被释放(state=0),则释放state的线程会唤醒等待队列中的线程继续尝试cas设值state;
- head:指向等待队列的头节点,延迟初始化,除了初始化之外,只能通过setHead方法进行修改;
- tail:指向等待队列的队尾,延迟初始化,只能通过enq方法修改tail,该方法主要是往队列后面添加等待节点。
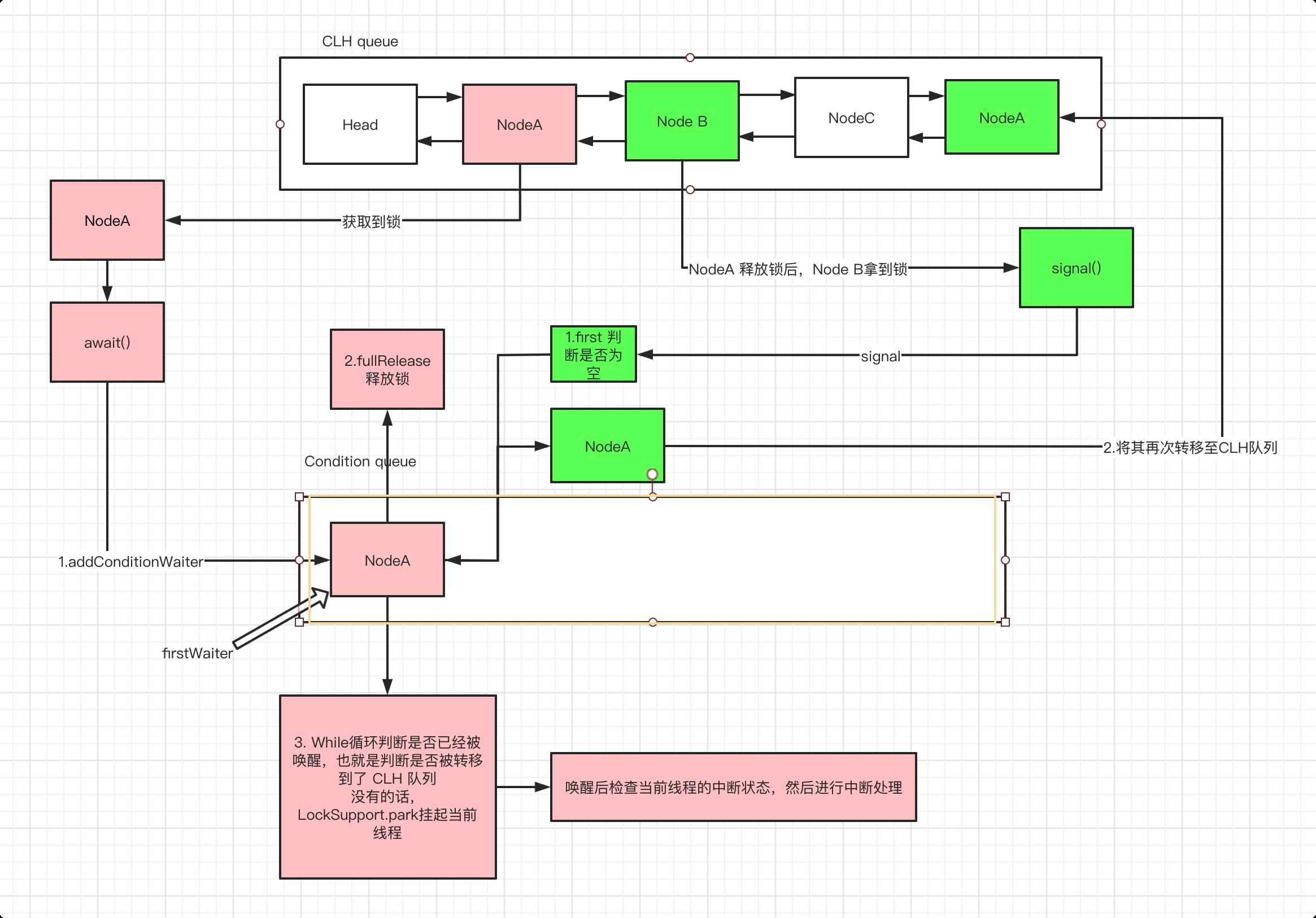
AQS队列节点数据结构

AQS中的一般处理流程
1.public final void acquire(int arg)
这个方法是使用独占模式获取锁,忽略中断。通过至少调用一次tryAcquire成功返回来实现。 否则,线程将排队,并可能反复阻塞和解除阻塞,并调用tryAcquire直到成功。
public abstract class AbstractQueuedSynchronizerextends AbstractOwnableSynchronizerimplements java.io.Serializable {public final void acquire(int arg) {// 尝试获取锁,这里是一个在AQS中未实现的方法,具体由子类实现if (!tryAcquire(arg) && // 获取不到锁,则 1.添加到等待队列 2.不断循环等待重试acquireQueued(addWaiter(Node.EXCLUSIVE), arg)) selfInterrupt();}
}
2.tryAcquire(int arg)
— 非公平锁在调用 lock 后,首先就会调用 CAS 进行一次抢锁,如果这个时候恰巧锁没有被占用,那么直接就获取到锁返回了。 非公平锁在CAS 失败后,和公平锁一样都会进入到 tryAcquire 方法,在 tryAcquire 方法中,如果发现锁这个时候被释放了(state== 0),非公平锁会直接 CAS 抢锁,但是公平锁会判断等待队列是否有线程处于等待状态,如果有则不去抢锁,乖乖排到后面。
公平锁和非公平锁就这两点区别,如果这两次 CAS 都不成功,那么后面非公平锁和公平锁是一样的,都要进入到阻塞队列等待唤醒。
相对来说,非公平锁会有更好的性能,因为它的吞吐量比较大。当然,非公平锁让获取锁的时间变得更加不确定,可能会导致在阻塞队列中的线程长期处于饥饿状态。
一开始,会尝试调用AQS中未实现的方法tryAcquire()尝试获取锁,获取成功则表示获取锁了,该方法的实现一般通过CAS进行设置state尝试获取锁:

不同的锁可以有不同的tryAcquire()实现,所以,你可以看到ReentrantLock锁里面会有非公平锁和公平锁的实现方式。
ReentrantLock公平锁的实现代码在获取锁之前多了一个判断:!hasQueuedPredecessors(),这个是判断如果当前线程节点之前没有其他节点了,那么我们才可以尝试获取锁,这就是公平锁的体现。
3. private Node addWaiter(Node mode)
获取锁失败之后,则会进入这一步,这里会尝试把线程节点追加到等待队列后面,是通过CAS进行追加的,追加失败的情况下,会循环重试,直至追加成功为止。如果追加的时候,发现head节点还不存在,则先初始化一个head节点,然后追加上去:
public abstract class AbstractQueuedSynchronizerextends AbstractOwnableSynchronizerimplements java.io.Serializable {private Node addWaiter(Node mode) {// 将当期线程构造成Node节点Node node = new Node(Thread.currentThread(), mode);// Try the fast path of enq; backup to full enq on failureNode pred = tail;if (pred != null) {// 将原来尾节点设置为新节点的上一个节点node.prev = pred;// 尝试用新节点取代原来的尾节点if (compareAndSetTail(pred, node)) {// 取代成功,则将原来尾指针的下一个节点指向新节点pred.next = node;return node;}}// 如果当前尾指针为空,则调用enq方法enq(node);return node;}
}
4.final boolean acquireQueued(final Node node, int arg)
加入等待队列之后,会执行该方法,不断循环地判断当前线程节点是否在head后面一位,如果是则调用tryAcquire()获取锁,如果获取成功,则把线程节点作为Node head,并把原Node head的next设置为空,断开原来的Node head。注意这个Node head只是占位作用,每次处理的都是Node head的下一个节点:
public abstract class AbstractQueuedSynchronizerextends AbstractOwnableSynchronizerimplements java.io.Serializable {/*** 已经入队的线程尝试获取锁*/ final boolean acquireQueued(final Node node, int arg) {//标记是否成功获取锁boolean failed = true;try {//标记线程是否被中断过boolean interrupted = false;for (;;) {//获取前驱节点final Node p = node.predecessor();//如果前驱是head,即该结点已成老二,那么便有资格去尝试获取锁if (p == head && tryAcquire(arg)) {// 获取成功,将当前节点设置为head节点setHead(node);// 原head节点出队,在某个时间点被GC回收p.next = null; // help GC//获取成功failed = false;//返回是否被中断过return interrupted;}// 判断是否需要阻塞线程,该方法中会把取消状态的节点移除掉,并且把当前节点的前一个节点设置为SIGNAL// 判断获取失败后是否可以挂起,若可以则挂起if (shouldParkAfterFailedAcquire(p, node) &&parkAndCheckInterrupt())// 线程若被中断,设置interrupted为trueinterrupted = true;}} finally {if (failed)cancelAcquire(node);}}
}
如果当前节点的pre不是head,或者争抢失败,则会将前面节点的状态设置为SIGNAL。
如果前面的节点状态大于0,表示节点被取消,这个时候会把该节点从队列中移除掉。
下图为尝试CAS争抢锁,但失败了,然后把head节点状态设置为SIGNAL:

然后再会循环一次尝试获取锁,如果获取失败了,就调用LockSupport.park(this)挂起线程。
那么时候才会触发唤起线程呢?这个时候我们得先看看释放锁是怎么做的了。
5.public final boolean release(int arg)
public abstract class AbstractQueuedSynchronizerextends AbstractOwnableSynchronizerimplements java.io.Serializable {public final boolean release(int arg) {//如果成功释放锁if (tryRelease(arg)) {//获取头节点:(注意:这里的头节点就是当前正在释放锁的节点)Node h = head;//头结点存在且等待状态不是取消if (h != null && h.waitStatus != 0)//唤醒距离头节点最近的一个非取消的节点unparkSuccessor(h);return true;}return false;}
}
tryRelease()具体由子类实现。一般处理流程是让state减1。
如果释放锁成功,并且头节点waitStatus!=0,那么会调用unparkSuccessor()通知唤醒后续的线程节点进行处理。
注意:在遍历队列查找唤醒下一个节点的过程中,如果发现下一个节点状态是CANCELLED那么就会忽略这个节点,然后从队列尾部向前遍历,找到与头结点最近的没有被取消的节点进行唤醒操作。

唤醒之后,节点对应的线程2又从acquireQueued()方法的阻塞处醒来继续参与争抢锁。并且争抢成功了,那么会把head节点的下一个节点设置为null,让自己所处的节点变为head节点:

这样一个AQS独占式、非中断的抢占锁的流程就结束了。
6.完整流程
最后我们再以另一个维度的流程来演示下这个过程。
首先有4个线程争抢锁,线程1,成功了,其他三个失败了,分别依次入等待队列:
线程2、线程3依次入队列:
现在突然发生了点事情,假设线程3用的是带有超时时间的tryLock,超过了等待时间,线程3状态变为取消状态了,这个时候,线程4追加到等待队列中后,发现前一个节点的状态是1取消状态,那么会执行操作把线程3节点从队列中移除掉:

最后,线程1释放了锁,然后把head节点ws设置为0,并且找到了离head最靠近的一个waitStatus<=0的线程并唤醒,然后参与竞争获取锁:
最终,线程2获取到了锁,然后把自己变为了Head节点,并取代了原来的Head节点:
参考
https://blog.csdn.net/a724888/article/details/60955965





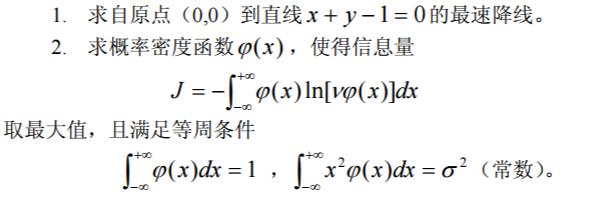
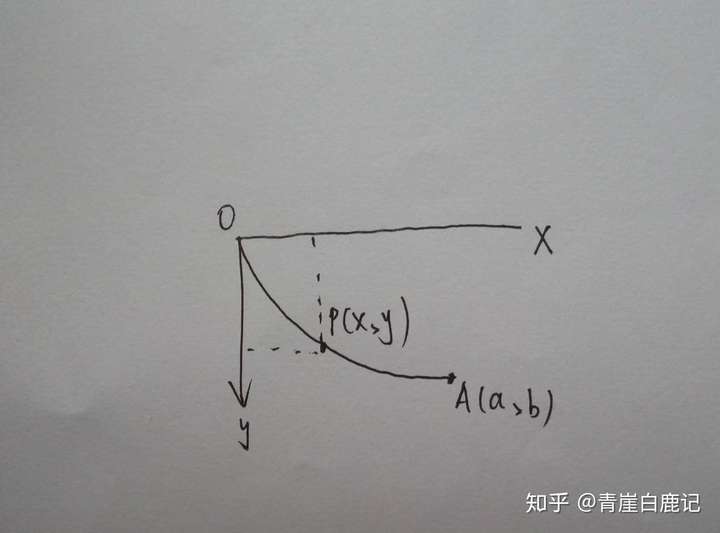

![[变分法介绍]优美的旋轮线:最速下降线问题,通过费马光学原理的初等证明](https://img-blog.csdnimg.cn/20200621210611999.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MzcwMDczMg==,size_16,color_FFFFFF,t_70#pic_center)