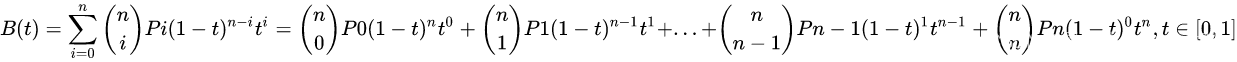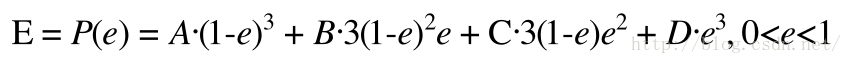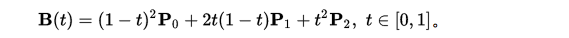文章目录
- 一、二阶贝塞尔曲线公式
- 二、三阶贝塞尔曲线
- 三、高阶贝塞尔曲线
贝塞尔曲线参考 : https://github.com/venshine/BezierMaker
一、二阶贝塞尔曲线公式
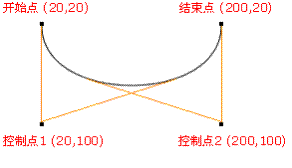
二阶贝塞尔曲线公式如下 :
B ( t ) = ( 1 − t ) 2 P 0 + 2 t ( 1 − t ) P 1 + t 2 P 2 , t ∈ [ 0 , 1 ] B(t) = (1- t)^2P_0 + 2t(1-t)P_1 + t^2P_2, t \in [0,1] B(t)=(1−t)2P0+2t(1−t)P1+t2P2,t∈[0,1]
P 0 , P 1 , P 2 P_0 , P_1 , P_2 P0,P1,P2 是给定的 平面中的 3 3 3 个点 , P 0 P_0 P0 是 曲线起始点 , P 2 P_2 P2 是 曲线结束点 , P 1 P_1 P1 是控制点 ;
t t t 的取值范围是 0.0 0.0 0.0 ~ 1.0 1.0 1.0 ;
二、三阶贝塞尔曲线
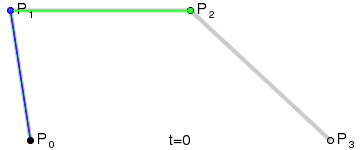
上图中 , P 0 P_0 P0 点是起始点 , P 3 P_3 P3 点是终止点 , P 1 P_1 P1 和 P 2 P_2 P2 点是控制点 ;
三阶贝塞尔曲线公式如下 :
B ( t ) = ( 1 − t ) 3 P 0 + 3 t ( 1 − t ) 2 P 1 + 3 t 2 ( 1 − t ) P 2 + t 3 P 3 , t ∈ [ 0 , 1 ] B(t) = (1- t)^3P_0 + 3t(1-t)^2P_1 + 3t^2(1-t)P_2 + t^3P_3, t \in [0,1] B(t)=(1−t)3P0+3t(1−t)2P1+3t2(1−t)P2+t3P3,t∈[0,1]
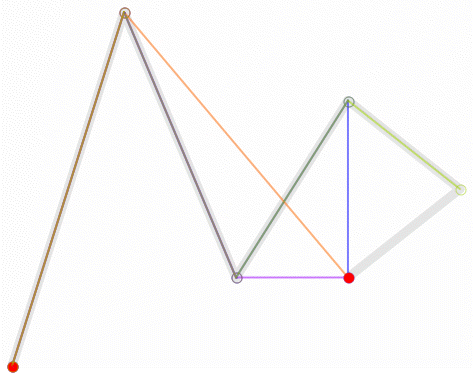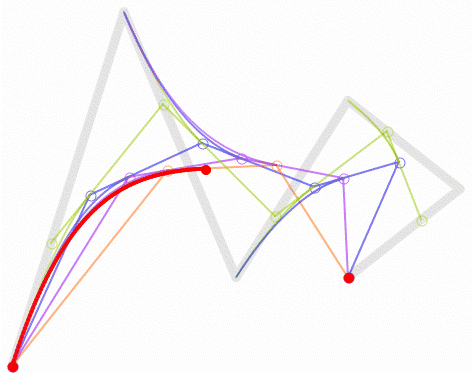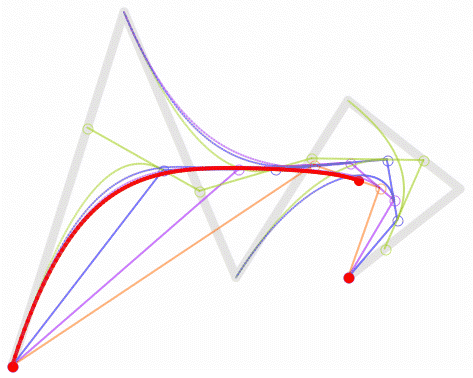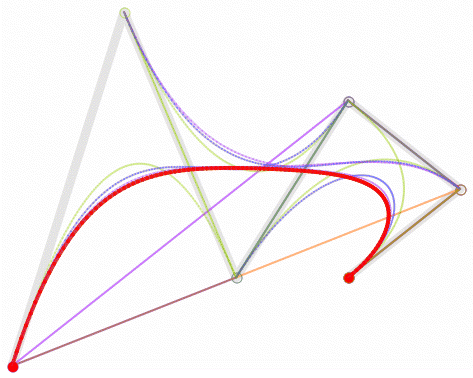
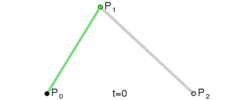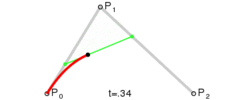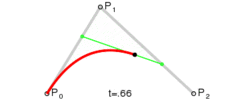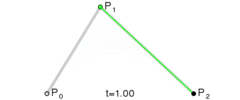
先根据比例 , 绘制出 P 0 P_0 P0 与 P 2 P_2 P2 之间的二阶贝塞尔曲线 , 以 P 1 P_1 P1 为控制点 , 绘制出直线 A B AB AB ;
然后 绘制 P 1 P_1 P1 与 P 3 P_3 P3 之间的二阶贝塞尔曲线 , 以 P 2 P_2 P2 为控制点 , 绘制出直线 B C BC BC ;
最后 计算 A A A 到 C C C 之间的 二阶贝塞尔曲线 , 以 B B B 点作为 控制点 ;
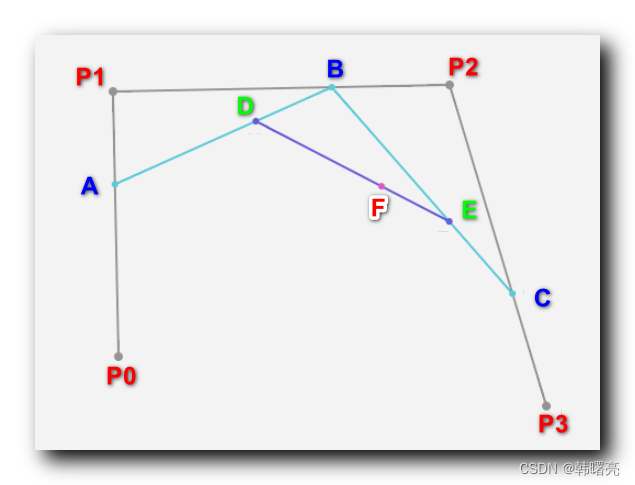
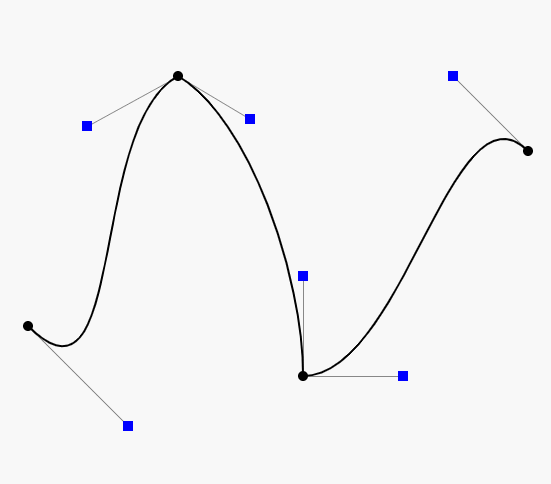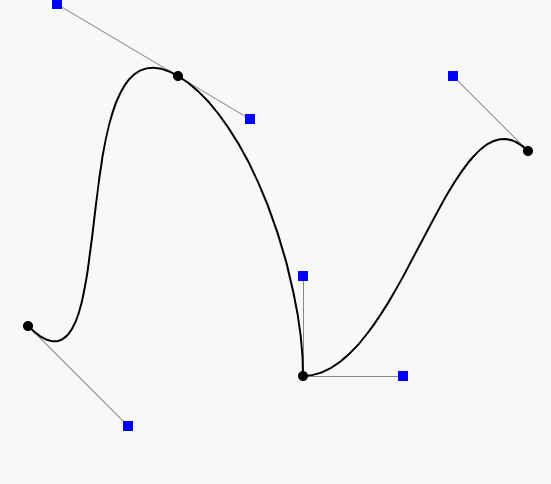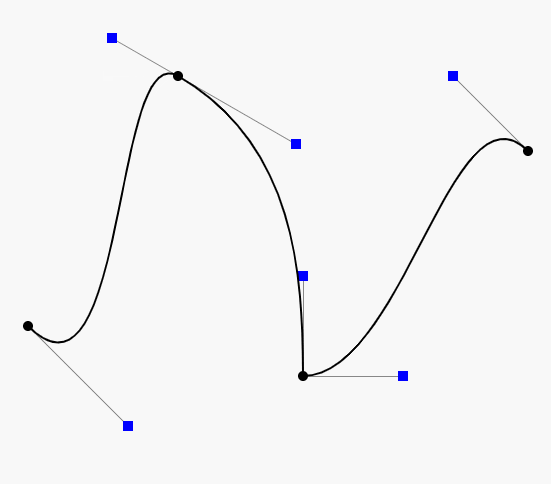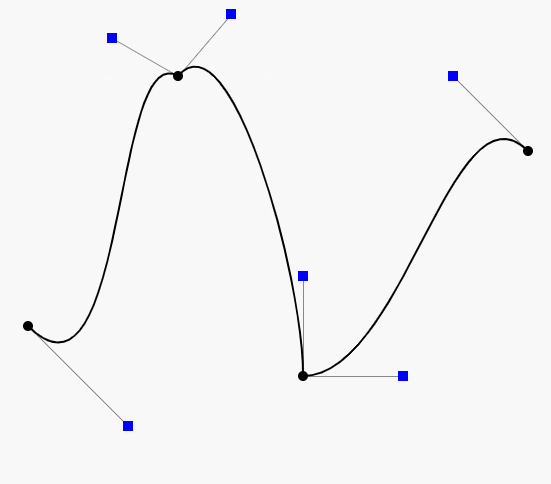
三阶贝塞尔曲线动态绘制流程 :

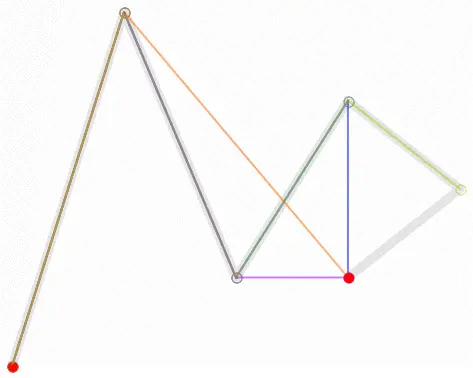
三、高阶贝塞尔曲线
B ( t ) = ∑ i = 0 n ( n i ) P i ( 1 − t ) n − i t i B(t) = \sum_{i = 0}^{n} \dbinom{n}{i} P_i (1-t)^{n - i}t^i B(t)=i=0∑n(in)Pi(1−t)n−iti
= ( n 0 ) P 0 ( 1 − t ) n t 0 + ( n 1 ) P 1 ( 1 − t ) n − 1 t 1 + ⋯ = \dbinom{n}{0} P_0 (1-t)^{n}t^0 + \dbinom{n}{1} P_1 (1-t)^{n - 1}t^1 + \cdots =(0n)P0(1−t)nt0+(1n)P1(1−t)n−1t1+⋯
+ ( n n − 1 ) P n − 1 ( 1 − t ) 1 t n − 1 + ( n n ) P n ( 1 − t ) 0 t n , t ∈ [ 0 , 1 ] + \dbinom{n}{n-1} P_{n-1} (1-t)^{1}t^{n -1} + \dbinom{n}{n} P_n (1-t)^{0}t^n , t \in [0,1] +(n−1n)Pn−1(1−t)1tn−1+(nn)Pn(1−t)0tn,t∈[0,1]
上述公式中 i i i 是贝塞尔曲线的阶数 ;
四阶贝塞尔曲线 :
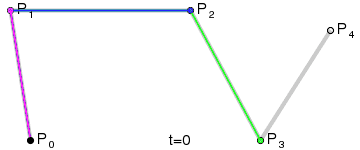
五阶贝塞尔曲线 :