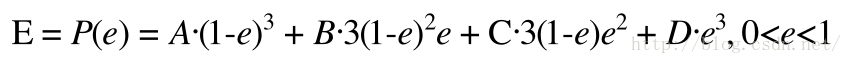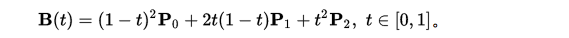贝塞尔曲线简介

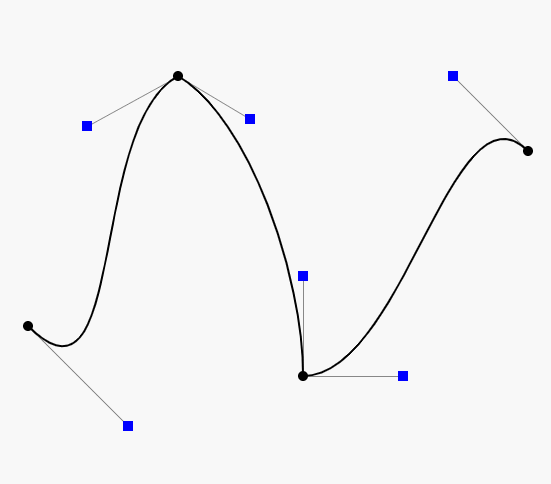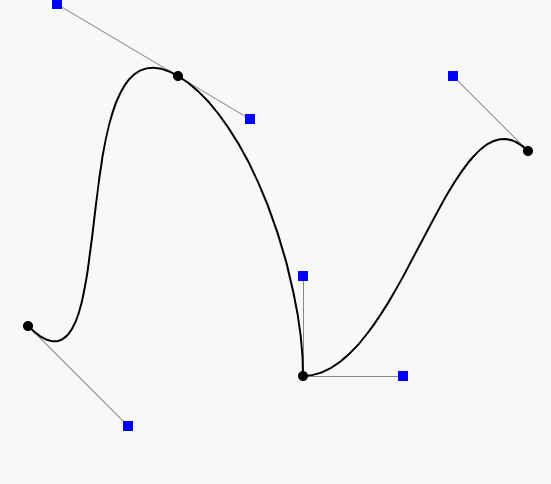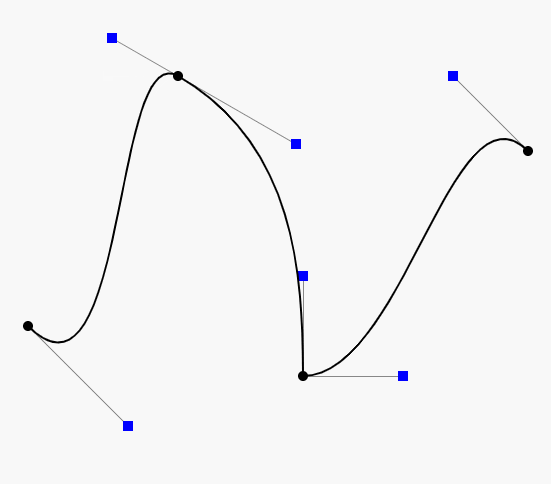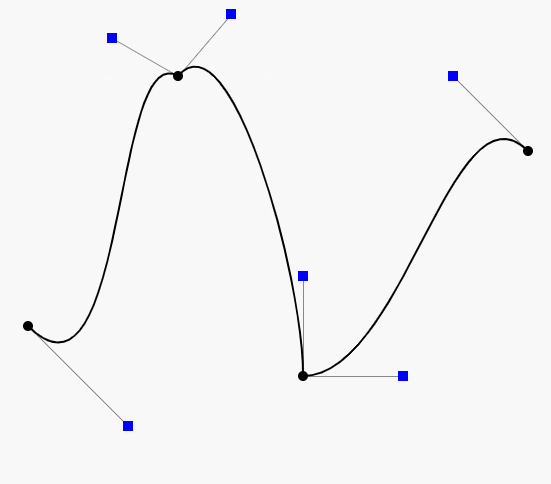
由于用计算机画图大部分时间是操作鼠标来掌握线条的路径，与手绘的感觉和效果有很大的差别。即使是一位精明的画师能轻松绘出各种图形，拿到鼠标想随心所欲的画图也不是一件容易的事。这一点是计算机万万不能代替手工的工作，所以人们只能颇感无奈。使用贝塞尔工具画图很大程度上弥补了这一缺憾。贝塞尔曲线是计算机图形图像造型的基本工具，是图形造型运用得最多的基本线条之一。它通过控制曲线上的四个点（起始点、终止点以及两个相互分离的中间点）来创造、编辑图形。
除此之外,贝塞尔曲线还经常用来做动画,让动画过渡更平滑。本文则记录如何使用贝塞尔曲线定制平滑的动画效果,并使用C++编写了cmd动画和窗口动画示例代码。

一阶贝塞尔

设定图中运动的点为Pt，t为运动时间，t∈(0,1)，可得如下公式:

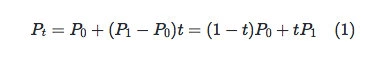
二阶贝塞尔

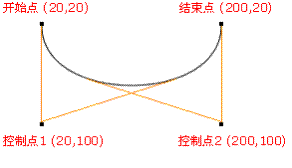
在二阶贝塞尔曲线中，已知三点恒定（P0,P1,P2），设定在P0 P1中的点为Pa，在P1 P2中的点为Pb，Pt在Pa Pb上的点，这三点都在相同时间t内做匀速运动。

由公式(1)可知

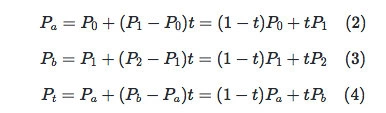
将公式(2)(3)代入公式(4)中，可得

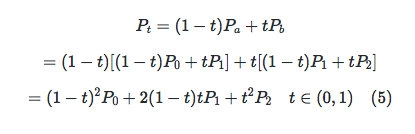
三阶贝塞尔

同理，根据以上的推导过程可得

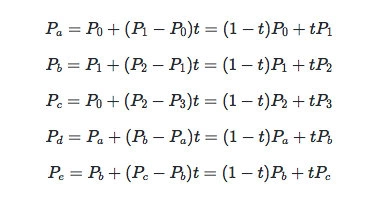
由此可以推导

N阶贝塞尔曲线

四阶贝塞尔曲线:

五阶贝塞尔曲线:

N阶贝塞尔曲线公式:

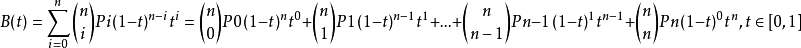
贝塞尔曲线在动画中的应用

• 贝赛尔曲线广泛应用于绘图软件中，例如Adobe PhotoShop、Adobe Flash。
• Android可以通过自定义的view来实现贝塞尔曲线
• ios则可以使用UIBezierPath类来生成贝塞尔曲线
• 前端，canvas bezierCurveTo，css animation-timing-function: cubic-bezier(x,x,x,x}都有关于贝赛尔曲线的一些应用。

贝塞尔曲线在动画中的应用一般是三阶贝塞尔曲线,通过两个控制点来描述一般的动画曲线。通常以动画完成度为y轴,时间为x轴,然后将时间带入动画曲线求得对应的动画完成度。

但是上述公式描述的是点与点关系,想要分解为x,y坐标的关系,则需要继续推导,以三阶为例:
想要直观的感受曲线的效果可以前往: cubic-bezier
得到x与y坐标关系后即可写代码进行实践了。

实践

求曲线散点坐标

由上面推导的曲线点的坐标和时间的关系可得:设曲线起点为(0,0),终点为(1,1),则t时刻点的位置仅与两个控制点P1 P2有关。先定义表示一个点的结构体:

  struct PointF{PointF() : x(0), y(0) {}PointF(double x, double y) : x(x), y(y) {}double x;double y;};

然后传入两个点的坐标进行初始化

  void init(double x1, double y1, double x2, double y2){pc.x = 3.0 * x1;pb.x = 3.0 * (x2 - x1) - pc.x;pa.x = 1.0 - pc.x - pb.x;pc.y = 3.0 * y1;pb.y = 3.0 * (y2 - y1) - pc.y;pa.y = 1.0 - pc.y - pb.y;}

计算t时刻的x和y坐标

  double calcX(double t){return ((pa.x * t + pb.x) * t + pc.x) * t;}double calcY(double t){return ((pa.y * t + pb.y) * t + pc.y) * t;}

根据给定的采样计算出[0,1]时刻的n个曲线上的点坐标,即可绘制出曲线图。

  for (int i = 0; i < size; ++i) { // size即为采样个数,然后计算出对应采样时刻的曲线坐标sample_[i] = PointF(calcX(i * 1.0 / size), calcY(i * 1.0 / size));}

得到曲线坐标后可绘制曲线图看下:

其中蓝色的曲线是贝塞尔曲线,绿色和红色的曲线分别表示贝塞尔曲线上的y坐标和x坐标与t的关系,即y随时间先慢,再快,最后慢。x随时间先快,再变慢,最后变快。

将曲线应用到动画

得到曲线散点坐标后,该怎么将其应用到动画呢?
因为我们已经设了x坐标在[0,1]之间,而动画一般就是分为动画完成度和时间的关系,而我们设动画的时间也在[0,1],那么就可以给定动画的时刻t,然后通过曲线散点坐标求得对应的动画完成度。
即通过x坐标求y坐标,因为我们只有散点坐标,时刻t不一定跟已有点的x坐标相同,因此需要找到最接近的时刻t的两个点进行插值,即可求得近似的y坐标,也即动画完成度。
废话不多说,直接上代码,使用二分法查找最近的两点并插值求y:

double GetYAtX(double x)
{int head = 0;int tail = size - 1;int center;while (head <= tail) {center = (head + tail) / 2;if (sample_[center].x < x) {head = center + 1;} else if (sample_[center].x > x) {tail = center - 1;} else {break;}}if (head < size - 1) {double x0 = sample_[head].x;double x1 = sample_[head + 1].x;double y0 = sample_[head].y;double y1 = sample_[head + 1].y;return (x - x0) / (x1 - x0) * (y1 - y0) + y0; // 线性插值计算} else {return 1;}
}

动画框架

现在时刻t的动画完成度能求了,接下来就是实验一下动画效果了,顺便封装一个简单的动画框架,这样就能方便的进行各种动画效果。

1. 首先封装一下贝塞尔曲线的求值,BezierCurve
2. 再封装做动画的类,Animator

封装完后即可开始使用

cmd动画

先来个cmd的动画试试,其中封装了个Console
示例代码:

int main()
{std::getc(stdin);std::thread thread([]() {draw::Rectangle r(10, 2);int fps = 70;int64_t interval = 1000 / fps;Animator animator(0, 150, 1, [&](int v) { r.SetPos(40 + v, 10);r.Draw();}, EasingCurve::Type::InOutBezier);auto last_time = std::chrono::steady_clock::now();bool forward = true;while (true) {while (!animator.Step(1.0 / fps, forward)) {auto now = std::chrono::steady_clock::now();auto delay = (interval - std::chrono::duration_cast<std::chrono::milliseconds>((now - last_time)).count());std::this_thread::sleep_for(std::chrono::milliseconds(delay > 0 ? delay : 1)); // 最低1ms免得卡last_time = std::chrono::steady_clock::now();}forward = !forward;}});thread.join();std::cout << std::endl;
}

分别实验了根据两种曲线进行动画的效果,通过cmd动画和网站上动画的对比,可以看出还是很接近的。

• InOutBezier: 参数(.63, 0, .37, 1)
  曲线图:
  
  效果图:
  

• InOutBounceBezier:参数(.56, -0.48, .46, 1.5)
  贝塞尔曲线:
  

  效果图:
  

窗口动画

• InOutBezier:参数(.63, 0, .37, 1)
  曲线图:
  
  效果图:
  

• InOutBounceBezier:参数(.56, -0.48, .46, 1.5)
  贝塞尔曲线:
  
  效果图:
  

完整代码

示例代码

贝塞尔动画(csdn下载)
贝塞尔动画(github)

核心类代码

BezierCurve

#pragma oncestruct BezierEase
{BezierEase(double x1, double y1, double x2, double y2){init(x1, y1, x2, y2);for (int i = 0; i < size; ++i) {sample_[i] = PointF(calcX(i * 1.0 / size), calcY(i * 1.0 / size));}}double value(double t){return GetYAtX(t);}double GetYAtX(double x){int head = 0;int tail = size - 1;int center;while (head <= tail) {center = (head + tail) / 2;if (sample_[center].x < x) {head = center + 1;} else if (sample_[center].x > x) {tail = center - 1;} else {break;}}if (head < size - 1) {double x0 = sample_[head].x;double x1 = sample_[head + 1].x;double y0 = sample_[head].y;double y1 = sample_[head + 1].y;return (x - x0) / (x1 - x0) * (y1 - y0) + y0; // 线性插值计算} else {return 1;}}
private:struct PointF{PointF() : x(0), y(0) {}PointF(double x, double y) : x(x), y(y) {}double x;double y;};double calcX(double t){return ((pa.x * t + pb.x) * t + pc.x) * t;}double calcY(double t){return ((pa.y * t + pb.y) * t + pc.y) * t;}void init(double x1, double y1, double x2, double y2){pc.x = 3.0 * x1;pb.x = 3.0 * (x2 - x1) - pc.x;pa.x = 1.0 - pc.x - pb.x;pc.y = 3.0 * y1;pb.y = 3.0 * (y2 - y1) - pc.y;pa.y = 1.0 - pc.y - pb.y;}PointF pa;PointF pb;PointF pc;const static int size = 1001;PointF sample_[size];
};

Animator

#pragma once#include "bezier_curve.h"class EasingCurve
{
public:enum Type{InOutBezier, InOutBounceBezier};EasingCurve(Type t){switch (t) {case InOutBounceBezier:curve_.reset(new BezierEase(.56, -0.48, .46, 1.5));break;case InOutBezier:curve_.reset(new BezierEase(.63, 0, .37, 1));default:break;}}// [0 - 1]double valueForProgress(double t){t = max(0, min(t, 1));return curve_->value(t);}
private:std::unique_ptr<BezierEase> curve_;
};template<typename T = int>
class Animator_
{
public:Animator_(T from, T to, double duration/*单位秒*/, std::function<void(T)> fn = nullptr, EasingCurve::Type type = EasingCurve::InOutBezier): ec_(type), from_(from), to_(to), duration_(duration), fn_(fn){}Animator_() : ec_(EasingCurve::InOutBezier) {}bool Step(double interval/*单位秒*/, bool forward = true){assert(interval > 0);double time_now = current_time_ + (forward ? interval : (-interval));bool isFinished = forward ? time_now >= duration_ : time_now <= 0;time_now = forward ? min(time_now, duration_) : max(time_now, 0);T val = duration_ == 0 ? (forward ? to_ : from_) : from_ + T((to_ - from_) *ec_.valueForProgress(time_now / duration_));current_time_ = time_now;if (fn_) fn_(val);return isFinished;}
public:void SetRange(T from_val, T to_value) { from_ = from_val; to_ = to_value; }void SetDuration(double val) { duration_ = val; }void SetFn(std::function<void(T)> val) { fn_ = val; }void ResetCurrentTime() { current_time_ = 0; }void SetCurrentTime(double current_time) { current_time_ = current_time; }void Complete(bool state_forward) { SetCurrentTime(state_forward ? duration_ : 0); }
private:T from_ = {};T to_ = {};double duration_ = 0;double current_time_ = 0;	//当前时间std::function<void(T)> fn_ = nullptr;EasingCurve ec_;
};using Animator = Animator_<>;

Console

#pragma once
#include <iostream>class Console
{
private:struct Cursor{public:// up down是y变化，x不变void up(int n = 1){std::cout << "\033[" << n << "A";}void down(int n = 1){std::cout << "\033[" << n << "B";}void right(int n = 1){std::cout << "\033[" << n << "C";}void left(int n = 1){std::cout << "\033[" << n << "D";}void save(){ // 保存当前位置std::cout << "\0337";}void restore(){ // 回到保存的位置std::cout << "\0338";}void nextLine(int n = 1){ // 光标以当前位置为起始位置，往下到第n行开头std::cout << "\033[" << n << "E";}void previousLine(int n = 1){ // 光标以当前位置为起始位置，网上到第n行开头std::cout << "\033[" << n << "F";}void move(int y = 0, int x = 0){ // 以当前屏幕为原点(0,0)移动光标std::cout << "\033[" << y << ";" << x << "H";}void enableBlinking(bool enable = false){std::cout << "\033[?12" << (enable ? "h" : "l");}void hideCursor(bool hide = true){std::cout << "\033[?25" << (hide ? "l" : "h");}};
public:Console(){const auto h_out = GetStdHandle(STD_OUTPUT_HANDLE);DWORD mode;GetConsoleMode(h_out, &mode);SetConsoleMode(h_out, mode | ENABLE_VIRTUAL_TERMINAL_PROCESSING);}enum Color{Black = 0,Red,Green,Yellow,Blue,Magenta,Cyan,White};void underline(){setTextAttr(4);}void noUnderline(){setTextAttr(24);}void bright(){ /* 设置前景颜色变亮 */setTextAttr(1);}void normal(){setTextAttr(0);}void negative(){ /* 前景色和背景色交换 */setTextAttr(7);}void positive(){ /* 将前景色和背景色恢复正常 */setTextAttr(27);}void setForeColor(Color color, bool bright = false){setTextAttr(bright ? 90 + color : 30 + color);}void setBackColor(Color color, bool bright = false){setTextAttr(bright ? 100 + color : 40 + color);}void setScrollRegion(int top, int bottom){std::cout << "\033[" << top << ";" << bottom << "r";}void clearCurLine(){std::cout << "\033[K";}void setTitle(const std::string &title){std::cout << "\033]2;" << title << "\x07";}int width(){auto info = getScreenBufferInfo();return info.srWindow.Right - info.srWindow.Left + 1;}int height(){auto info = getScreenBufferInfo();return info.srWindow.Bottom - info.srWindow.Top + 1;}
public:Cursor cursor;private:void setTextAttr(int n){std::cout << "\033[" << n << "m";}CONSOLE_SCREEN_BUFFER_INFO getScreenBufferInfo(){CONSOLE_SCREEN_BUFFER_INFO info;GetConsoleScreenBufferInfo(GetStdHandle(STD_OUTPUT_HANDLE), &info);return info;}
};

参考资料

1. 从零开始学图形学：10分钟看懂贝塞尔曲线
2. 如何理解并应用贝塞尔曲线
3. JS模拟CSS3动画-贝塞尔曲线
4. 求高手解答 贝塞尔曲线问题
5. cubic-bezier:贝塞尔曲线在线预览网站