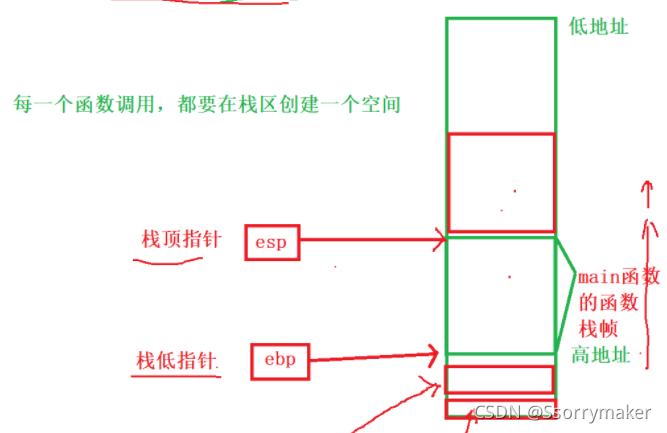
有兴趣的建议看这篇，比较新：https://zhuanlan.zhihu.com/p/366678047

曲线和曲面

在生活中存在着各种各样光滑的曲线或曲面，例如汽车的表面，钢珠球等。

在建模的时候，我们通常使用很多的小三角形来逼近这样的曲面，因此放大了看，就会发现这些面其实是凹凸不平的。但是实际生活中，例如我身边的杯子，无论怎么看它都是一个光滑的表面。

那么我们应该怎么表达这些光滑的曲线或曲面呢？我们先从曲线入手，看看它的几种表达方式。

曲线的显示表示（Explicit representation）

学过函数我们知道， $y=x^2$ 画出来的图其实就是一条曲线，如下：

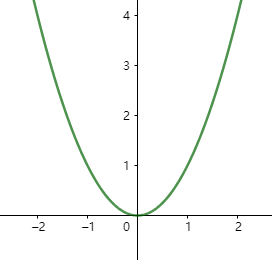
当然还有 $y=x^3+k$ 等等函数，可以画出各式各样的曲线。这种 y=f(x) 的表达方式，我们称之为二维空间中，曲线的显示表示。即以自变量（x）来表达因变量（y）的值。

曲线的隐式表示（Implicit representation）

隐式表示，就是利用隐式方程来刻画一条曲线，在二维空间中一个隐式的曲线可以通过 f(x,y)=0 来表达。例如圆的隐式方程即为： $x^2+y^2-r^2=0$ ，用它即可表示一个半径为 r 的圆。

曲线的参数形式表示（Parametric form）

该形式也是图形学里最关心和最常用的形式。一个曲线的参数形式是通过一个自变量（参数） t 来表达曲线上每个点的空间坐标。

在三维空间中，我们可以用如下三个显示的函数，来表示一条空间曲线。

x=x(t)
y=y(t)
z=z(t)

t=0即代表曲线的起点，t=1代表曲线的终点，因此可以用 t （0<=t<=1）代表曲线上的任意一点 P(t)，然后将 t 的值带入三个显示的方程，即可求出曲线上点 P 的坐标，P(t) = (x(t), y(t), z(t)) 。

参数曲线并不是唯一的，一个给定的曲线或者曲面可以通过不同的形式表达。给定一个表达式我们可以画出一个唯一的曲线，但是该曲线可能还有别的表达式可以来表示。

参数形式有一个好处，例如上面的式子表达的是三维空间的曲线，如果我们删除了 z=z(t)，那么它就变成了一个二维空间的曲线，即降维很方便。并且同样的也容易推广到高维，新增新维度对应的显示方程即可。

并且前面我们说了 t 的范围是 0-1，并且代表曲线上的一点，那么我们只需要将 t 的值慢慢从 0 变到 1 ，点就会沿着曲线行走，我们就可以得到曲线的轨迹，容易实现曲线的绘制。

此外我们还可以对每个点求导，即 $\frac{dP(t)}{dt}=(\frac{dx(t)}{dt},\frac{dy(t)}{dt},\frac{dz(t)}{dt})$ ，得到结果被视为曲线的绘制速度，该导数指向曲线的切向。

举个二维的例子，比方说我有一个 $y=0.3x^2+1$ 的曲线，其中 x 的取值范围为 1-4，那么这个曲线如下图：

我们来看看怎么用参数的形式来表示，首先是 x 和 t 的关系，因为 x 是 1-4，而 t 是 0-1，因此我们可得到方程 x = 3t+1 。然后是 y，因为我们知道这个曲线是 $y=0.3x^2+1$ 的，因此我们把里面的 x 用 x=3t+1 来代替即可，得到 $y=0.3(3t+1)^2+1=2.7t^2+1.8t+1.3$ 。因此我们上诉曲线的参数形式即为：

x = 3t+1
$y=2.7t^2+1.8t+1.3$

通过带入不同的 t 值，即可得到该曲线各个点的坐标，例如 P(0)=(1, 1.3)，P(1)=(4, 5.8)。

参数形式与多项式

我们曲线的参数形式写成一个多项式的形式。例如我们前面的二维例子，我们可以把它写成一个二阶的多项式，即 $at^2+bt+c$ 的形式。但是其中a，b，c并不是常数，而是代表着向量，其结果为： $P(t)=(0,2.7)t^2+(3,1.8)t+(1,1.3)$ 。

对于3阶多项式参数曲线具有如下形式： $P(t)=at^3+bt^2+ct+d$ ，它被称为Ferguson曲线，曾被用于美国早期的飞机设计中。

但是我们也可以发现，这种多项式的表达方式并不直观。而且 t 之前的系数也并不好算，即是给定了这些系数，也很难想象出曲线的形状。

因此后面就有了贝塞尔曲线。

贝塞尔曲线（Bezier Curve）

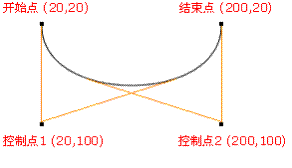
相比之前的几种曲线表示方法，贝塞尔提出的是一种通过连接向量（connected vectors）来表示曲线的方法，如下：

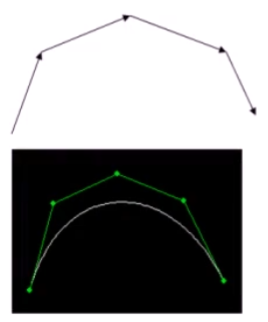
即在画曲线前先通过向量绘制一个多边形，代表该曲线的趋势和走向。就好比画画的时候先画个大致轮廓再画细节，雕刻的时候也是先雕个大致形状再慢慢打磨。并且贝塞尔曲线具有交互性，也就是说我们可以通过修改向量，来修改曲线。

贝塞尔提出了如下公式用于计算曲线，将曲线表达成向量和基函数的乘积。

$V(t)=\sum_{i=0}^{n}f_{i,n}(t)A_i$

其中 $A_i$ 代表的就是向量， $f_{i,n}(t)$ 代表的是一个基函数，其内容如下：

$f_{i,n}(t)=\left\{\begin{matrix} 1 &&i=0\\ \frac{(-t)^i}{(i-1)!}\frac{d^{i-1}}{dt^{i-1}}\frac{(1-t)^{n-1}-1}{t} \end{matrix}\right.$

注：该基函数本质上就是一个n-1次的多项式。

有了这个公式后，也就是说你给我一个多边形，我就可以用它算出一个曲线，从公式中我们也可发现，贝塞尔曲线属于一种参数形式表示曲线的方式。

伯恩斯坦多项式

1972年，Forrest在Computer Aided Design杂志上发表了他的著名论文，在论文里他指出贝塞尔曲线可以借助伯恩斯坦多项式被定义在点集上。

有关伯恩斯坦多项式的介绍可以参考：https://zhuanlan.zhihu.com/p/366082920

原本贝塞尔曲线说的是向量相连，我们现在把这向量都变成一个个控制点，即给定控制顶点 $P_0,P_1,P_2...P_n$ ，贝塞尔曲线可以定义为：

$P(t)=\sum_{i=0}^{n}P_iB_i^n(t)$

其中的 $B_i^n(t)$ 就是第 i 个 n 阶的伯恩斯坦多项式：

$B_i^n(t)=C_n^it^i(1-t)^{n-i}$

$C_n^i=\frac{n!}{i!(n-i)!}$

其中 $C_n^i$ 组合数，所以贝塞尔曲线的很多算法和定理，都是在弄这个组合公式。

贝塞尔曲线的绘制

通过前面的介绍，也就是说我们的贝塞尔曲线可以通过一堆控制点来画出，那么假如我们有如下三个控制点，我们怎么来画出一个贝塞尔曲线呢？

前面我们说了，参数形式的表达，是对曲线上各个点坐标的表达，那么我们只需要根据这些控制点依照 t 的变换求出对应的点，即可求出曲线上所有的点，从而形成曲线。

那么问题就变成了我知道控制点和 t 的值，求曲线上对应的点 P(t) 的坐标是多少。

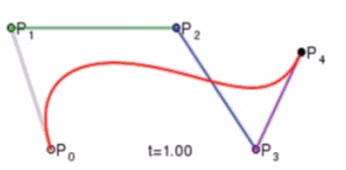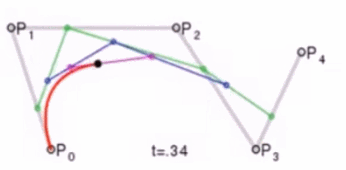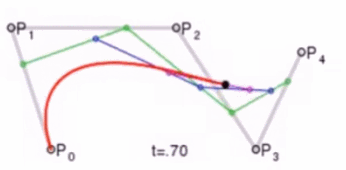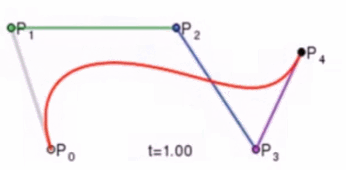
这个问题我们可以使用德卡斯特里奥算法（de Casteljau Algorithm）来解决。

那么怎么利用该算法求P(t)呢？我们先把 $P_0,P_1,P_2...P_n$ 连线，例子中就三个点，连线如下：

例如 $P_0P_1$ 线段，通过线性插值在线段上找到点 $P_{0,1}$ ，使得 $P_0P_{0,1}:P_{0,1}P1=t:1-t$ ，其他线段也如此，我们就可得到下图

然后我们连接 $P_{0,1}P_{1,1}$ ，得到新的线段，然后在该线段上再取一点使得该线段被分为 t 和 1-t，那么就会得到下图：

此时已经不能再连线了，而我们得到的点 $P_{0,2}$ 就是这三个控制点对应的贝塞尔曲线在 t 位置上的点。这样我们就可以通过使 t 从0变到1，得到所有曲线上的点，从而得到曲线。这样的求曲线上任意一点方式也就是de Casteljau算法。

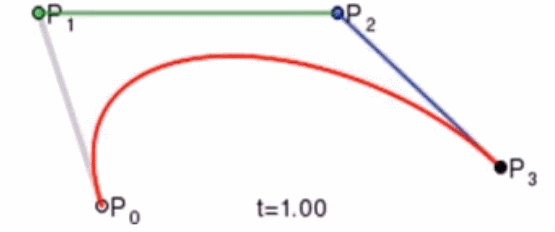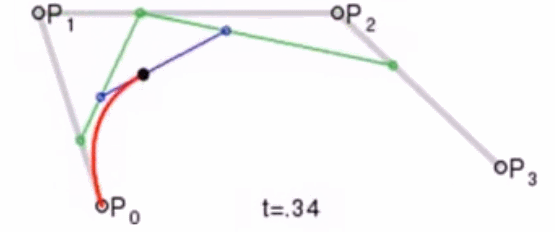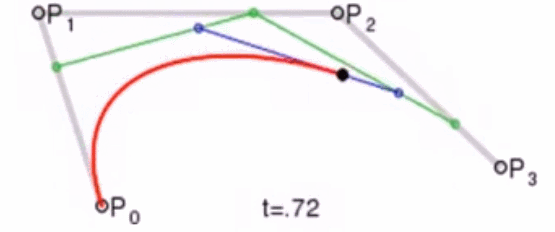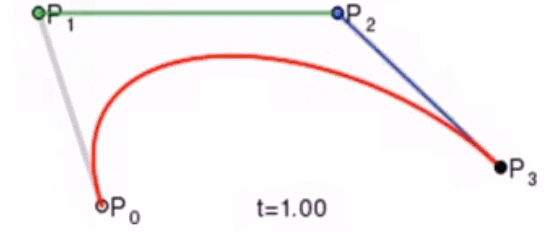
如果有更多的控制点，我们也可以使用相同的方法来求出曲线上的一点，如下图是四个控制点求曲线上一点的过程：

对于三个顶点控制的贝塞尔曲线我们称之为二阶贝塞尔曲线（Quadratic Bezier），那么四个顶点自然是三阶贝塞尔曲线（Cubic Bezier），因此 n 阶贝塞尔曲线有 n+1 个顶点。而de Casteljau算法则是把这 n+1 个点，先变成 n 个新的点，然后在变成 n-1 个新的点，这些新的点都可以用对应的控制点和 t 线性插值得到，最终得到一个点，这个点就是贝塞尔曲线上的点。

如下动图，很直接明了的表示了贝塞尔曲线的绘制过程：

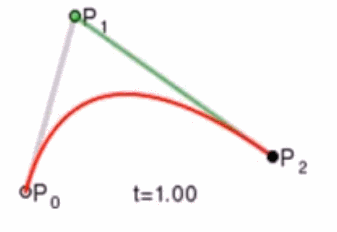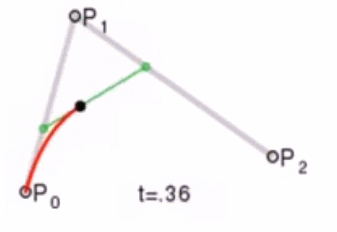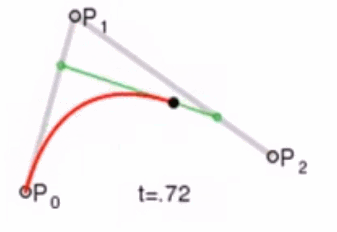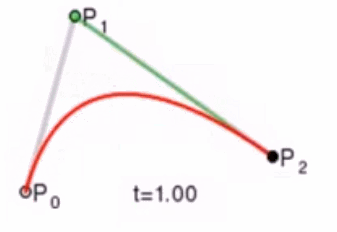
伯恩斯坦多项式与de Casteljau算法

过程也说了，图也看了，回到公式部分，我们来看看伯恩斯坦多项式与de Casteljau算法的关系。我们拿最简单的二阶贝塞尔曲线举例，如下图：

图中蓝色的点为控制点，他们的坐标我们是知道的，那么通过线性插值，我们可以得到求出红色点的坐标，公式如下（ $P_{x,y}$ 我们用 $P_x^y$ 来代替）：

$P_0^1=(1-t)P_0+tP_1$

$P_1^1=(1-t)P_1+tP_2$

红色点坐标求出后，我们自然可以再求出绿色点的坐标：

$P_0^2=(1-t)P_0^1+tP_1^1$

把上面两个式子带入到下面的式子，得到：

$P_0^2=(1-t)((1-t)P_0+tP_1)+t((1-t)P_1+tP_2)$

$=(1-t)^2P_0+2t(1-t)P_1+t^2P_2$

我们还可以用这个方法去算三阶的，四阶的，乃至n阶的贝塞尔曲线，得到的结果为曲线上任意一点P(t)是各个顶点的线性组合，即：

$P(t)=k_0P_0+k_1P_1+k_2P_2+...+k_nPn$

而我们每个顶点前面的系数k，就是伯恩斯坦多项式。例如二阶贝塞尔曲线对应的伯恩斯坦多项式为 $B_i^2(t)$ ，其中 $B_0^2(t)=(1-t)^2$ ， $B_1^2(t)=2t(1-t)$ ， $B_2^2(t)=t^2$ ，正好对应前面的三个系数。

因此可以得出结论，对于 n 阶的贝塞尔曲线，曲线上 t 位置上的点 P(t) 的坐标是由 n+1 个顶点和伯恩斯坦多项式的乘积求和：

$P(t)=B_0^n(t)P_0+B_1^n(t)P_1+B_2^n(t)P_2+...+B_n^n(t)Pn=\sum_{i=0}^{n}P_iB_i^n(t)$

上面式子也就是Forrest在1972年提出的结论。因此我们就可以使用de Casteljau算法来算曲线上任意一点的坐标，该算法是计算伯恩斯坦多项式的一种递归算法，直接方法相比较慢，但它在数值上更为稳定。

前面我们是从线性插值计算，逆推到伯恩斯坦多项式。现在我们来看看怎么直接使用伯恩斯坦多项式得到递归的结果。

在讲到伯恩斯坦多项式的时候，我们说它具有递归性，即可以把 n 阶的伯恩斯坦多项式写成 n-1 阶的多项式组合：

$B_i^n(t)=(1-t)B_i^{n-1}(t)+tB_{i-1}^{n-1}(t)$

也就是说原本的方程式：

$P(t)=B_0^n(t)P_0+B_1^n(t)P_1+B_2^n(t)P_2+...+B_n^n(t)Pn$

可以写成：

$P(t)=(1-t)B_0^{n-1}(t)P_0+((1-t)B_1^{n-1}(t)+tB_0^{n-1}(t))P_1+\\((1-t)B_2^{n-1}(t)+tB_1^{n-1}(t))P_2+...+tB_{n-1}^{n-1}(t)Pn$

我们单独来看，会发现里面有 $(1-t)B_0^{n-1}(t)P_0+tB_0^{n-1}(t)P_1$ ，我们提取一下不就变成了 $B_0^{n-1}((1-t)P_0+tP_1)$ ，而 $((1-t)P_0+tP_1)$ 是啥子？不就是两点的线性插值么。对于后面的几项也是一样的，上面式子就可以写成：

$P(t)=((1-t)P_0+tP_1)B_0^{n-1}(t)+((1-t)P_1+tP_2)B_1^{n-1}(t)+((1-t)P_2+tP_3)B_2^{n-1}(t)+...+((1-t)P_{n-1}+tP_n)B_{n-1}^{n-1}(t)$

那么就可以把贝塞尔曲线的方程式写成：

$P(t)=\sum_{i=0}^{n}P_i((1-t)B_i^{n-1}(t)+tB_{i-1}^{n-1}(t))=\sum_{i=0}^{n-1}((1-t)P_i+tP_{i+1})B_i^{n-1}(t)$

也就是说我们把原本 n 个控制点，通过 $((1-t)P_i+tP_{i+1})$ 变成了 n-1 个新的控制点。那么 n-1 个控制点又可以按这个方法变成 n-2 个控制点，一直递归下去，最终只剩一个控制点，也就是曲线上的点。这个方法也正是我们之前贝塞尔曲线的绘制过程。

端点性质

伯恩斯坦多项式具有端点性质，贝塞尔曲线同样具有，其实从绘制过程中，我们就很容易看出来，曲线是从第一个控制点开始到最后一个控制点结束的，即：

$P(0)=P_0$

$P(1)=P_n$

切向量（Tangent Vector）

切向量也就是对贝塞尔曲线求导，我们知道伯恩斯坦多项式的求导公式如下：

$B_i^{n'}(t)=n(B_{i-1}^{n-1}(t)-B_i^{n-1}(t))$

那么贝塞尔曲线的求导结果即为：

$P'(t)=n\sum_{i=0}^{n-1}P_i(B_{i-1}^{n-1}(t)-B_i^{n-1}(t))$

我们先来看看 t=0 的情况，可得： $P'(0)=n(P_0(-B_0^{n-1}(0)))+P_1(B_0^{n-1}(0)-B_1^{n-1}(0))+P_2(B_1^{n-1}(0)-B_2^{n-1}(0))+...)$

由于伯恩斯坦多项式的端点性质：

$B_i^n(0)\left\{\begin{matrix}=1&&i=0 \\ =0&&otherswise \end{matrix}\right.$

所以

$P'(0)=n(P_1-P_0)$

同理也可证明，当 t=1 时：

$P'(n)=n(P_n-P_{n-1})$

也就是说贝塞尔曲线在起点处的切向量方向就是 $P_0$ 到 $P_1$ 的方向，终点处的切向量方向就是 $P_{n-1}$ 到 $P_n$ 的方向，如下图：

通过公式，也很好理解为什么三阶的贝塞尔曲线起点和终点的切向量前面有个系数3了。

二阶导数

同样的，我们还可以求贝塞尔曲线的二阶导数，公式如下（这里就不推导了，简单的记个笔记）：

$P''(t)=n(n-1)\sum_{i=0}^{n-2}(P_{i+2}-2P_{i+1}+P_i)B_i^{n-2}(t)$

因此：

$P''(0)=n(n-1)(P_2-2P_1+P_0)$

$P''(1)=n(n-1)(P_n-2P_{n-1}+P_{n-2})$

有了一阶和二阶导数，我们就可以算出曲率，曲率是微分几何里面描述曲线弯曲程度的概念。通过曲率公式可得：

$k(0)=\frac{n-1}{n}*\frac{|(P_1-P_0)\times(P_2-P_1)|}{|P_1-P_0|^3}$

$k(1)=\frac{n-1}{n}*\frac{|(P_{n-1}-P_{n-2})\times(P_n-P_{n-1})|}{|P_n-P_{n-1}|^3}$

k阶导数

贝塞尔曲线的 k 阶导数的差分形式如下：

$P^k(t)=\frac{n!}{(n-k)!}\sum_{i=0}^{n-k}\bigtriangleup ^kP_iB_i^{n-k}(t)$

$\bigtriangleup ^kP_i$ 代表着 k 阶差分，定义如下：

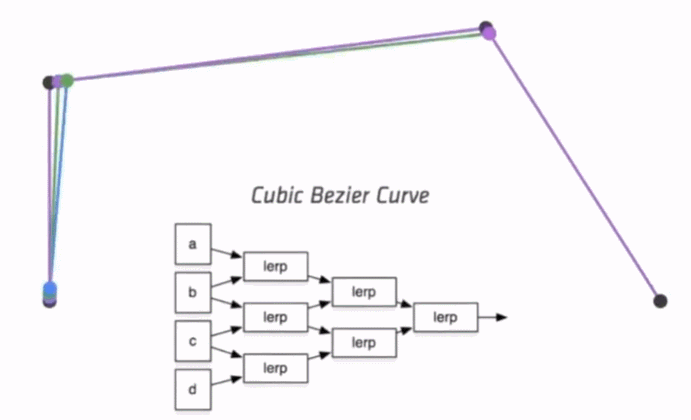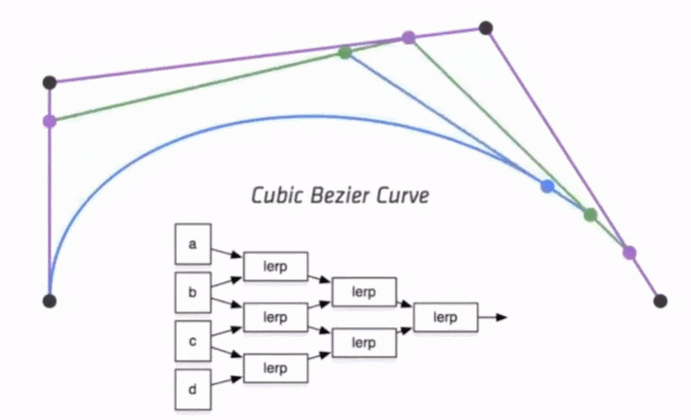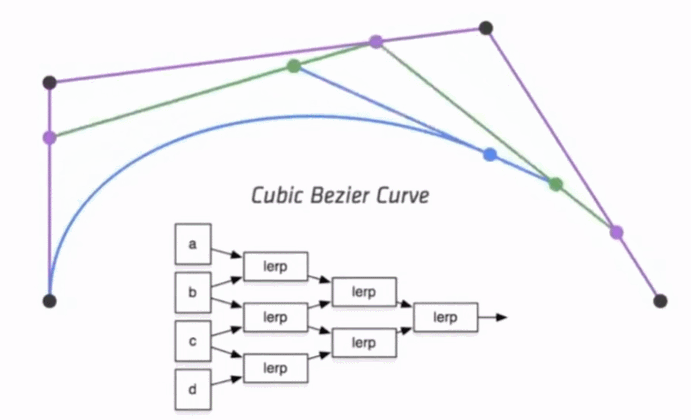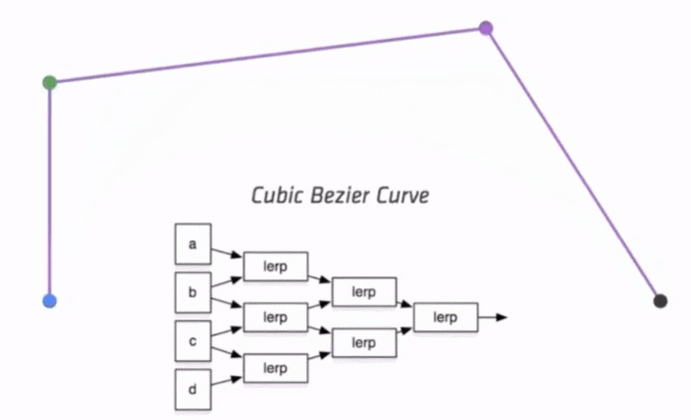
$\bigtriangleup ^kP_i=\left\{\begin{matrix} P_i&&k=0\\ \bigtriangleup ^{k-1}P_{i+1}-\bigtriangleup ^{k-1}P_i \end{matrix}\right.$

对称性

因为伯恩斯坦多项式有对称性，因此贝塞尔曲线同样拥有对称性。也就是说我们把 $P_0,P_1,P_2...P_n$ 这些顶点顺序倒过来，求得的曲线和之前的曲线一模一样，只是方向相反，如下图，很容易可以看出缩回来的时候（顺序相反），路径是一样的：

凸包性（Convex Hull）

根据伯恩斯坦多项式的归一性，我们可以得出贝塞尔曲线的凸包性，也就是说贝塞尔曲线必定在所有控制点的凸包内部。

所谓凸包即是可以包含所有顶点的最小凸多边形，如下图：

黑色的点是我们的控制点，那么蓝色的形状就是这些控制点的凸包。我们可以把这些控制点想象成木板上的钉子，蓝色的线是一根可拉到无限大的橡皮筋，当我们把橡皮筋拉到包含所有顶点的时候，一松手，橡皮筋收缩后形成的形状就是凸包。

几何不变性（Geometric invariance）

即贝塞尔曲线的一些几何性质不随坐标系变换，因为贝塞尔曲线的位置和性质依赖于控制点，而不是坐标系。

仿射变换

对贝塞尔曲线做仿射变换，我们可以通过先对控制点做仿射变换，然后利用变换后的控制点来得到新的曲线，这个曲线和直接对曲线做仿射变换得到的结果是一样的。

但是需要注意，投影变换不能这么操作。

升阶操作

所谓升阶操作，就是比如我们原本由 n+1 个控制点得到一个 n 阶贝塞尔曲线，我们可以把它变成是 n+2 个新的控制点并且得到 n+1 阶的贝塞尔曲线，这两个曲线一模一样。

升阶操作的好处在于可以增加灵活性，例如我们原本有一个二阶的贝塞尔曲线，想要改变曲线形状只能修改三个顶点的位置。但是通过升阶，把它变成三阶的四阶的乃至更高阶的，我们就可以通过更多的顶点来调整这个曲线。

伯恩斯坦多项式的升阶公式如下：

$B_i^n(t)=(1-\frac{i}{n+1})B_i^{n+1}(t)+(\frac{i+1}{n+1})B_{i+1}^{n+1}(t)$

那么 $P(t)=B_0^n(t)P_0+B_1^n(t)P_1+B_2^n(t)P_2+...+B_n^n(t)Pn$ 就可以写成如下形式：

$P(t)=((1-\frac{0}{n+1})B_0^{n+1}(t)+\frac{1}{n+1}B_1^{n+1}(t))P_0+((1-\frac{1}{n+1})B_1^{n+1}(t)+\frac{2}{n+1}B_2^{n+1}(t))P_1+((1-\frac{2}{n+1})B_2^{n+1}(t)+\frac{3}{n+1}C_3^{n+1}(t))P_2+...+((1-\frac{n}{n+1})B_n^{n+1}(t)+(\frac{n+1}{n+1})B_{n+1}^{n+1}(t))P_n$

首先我们先看头尾， $((1-\frac{0}{n+1})B_0^{n+1}(t)P_0=B_0^{n+1}(t)P_0$ 和 $(\frac{n+1}{n+1})B_{n+1}^{n+1}(t)P_n=B_{n+1}^{n+1}(t)P_n$ 。

然后我们再看其他几项，其中 $\frac{1}{n+1}B_1^{n+1}(t)P_0+(1-\frac{1}{n+1})B_1^{n+1}(t)P_1$ ，提取一下不就是 $B_1^{n+1}(t)(\frac{1}{n+1}P_0+(1-\frac{1}{n+1})P_1)$ ，而 $\frac{1}{n+1}P_0+(1-\frac{1}{n+1})P_1$ 不就又是一个线性插值的点么，也就是升阶后的新点。往后也是，每两个控制点会线性插值出一个新的点，那么 n+1 个控制点不就可以生成 n 个新的控制点么。新的控制点 $P_i^*$ 的公式如下：

$P_i^*=\frac{i}{n+1}P_{i-1}+(1-\frac{i}{n+1})P_{i}$

那么我们新的式子就可以写成：

$P(t)=B_0^{n+1}(t)P_0+B_1^{n+1}(t)(\frac{1}{n+1}P_0+(1-\frac{1}{n+1})P_1)+B_1^{n+1}(t)(\frac{2}{n+1}P_1+(1-\frac{2}{n+1})P_2)+...+B_i^{n+1}(t)(\frac{i}{n+1}P_{i-1}+(1-\frac{i}{n+1})P_{i})+...+B_{n+1}^{n+1}(t)P_n$

也就是说头尾两个控制点不变，中间生成 n 个新的控制点，这样原本 n+1 个控制点就变成了 n+2 个控制点，实现了升阶操作。

升阶公式最终如下：

$P(t)=\sum_{i=0}^{n}P_i((1-\frac{i}{n+1})B_i^{n+1}(t)+(\frac{i+1}{n+1})B_{i+1}^{n+1}(t))$

$=\sum_{i=0}^{n+1}((1-\frac{i}{n+1})P_i+\frac{i}{n+1}P_{i-1})B_i^{n+1}(t)$

下图为升阶的效果图：

从图中可以发现，当升阶的次数越多，顶点形成的线条就会越逼近曲线本身，在微积分里有个Weierstrass逼近定理：一个连续函数总是可以用一个多项式无限逼近，我们的升阶操作就等于证明了这个定理（该定理本质上就可以用伯恩斯坦多项式来证明）。

但是这里其实有个问题，我们之前说切向量的时候，说贝塞尔曲线顶点和终点的切向量是第一个和最后一个控制点的方向。但是如上图，我们曲线没变，等于切向量没变，但是随着控制点增加，控制点的方向一直在变，这不是违背了么？实际上我们将一个 n 阶的贝塞尔曲线升阶，不管升多少次，它本质上（代数上）还是n阶的，升阶只是给它换了个表现形式。

降阶操作

降阶的目的是寻找一组新的控制点定义的曲线，使得误差最小。

降阶是升阶的逆过程，我们假设 n 阶贝塞尔曲线（控制点为 $P_i$ ）是 n-1 阶贝塞尔曲线（控制点为 $P_i^*$ ）的升阶结果，根据升阶公式我们可以得到：

$P_i=\frac{i}{n}P_{i-1}^*+(1-\frac{i}{n})P_{i}^*$

那么我们就可以得到下面两个递推公式（下面的公式1用 $P_i^{%}$ 表示降阶后的顶点，公式2用 $P_i^*$ ）：

$P_{i}^%=\frac{nP_i-iP_{i-1}^%}{n-i}$ 其中 i = 0, 1, ..., n-1

$P_{i-1}^*=\frac{nP_i-(n-i)P_{i}^*}{i}$ 其中 i = n, n-1, ..., 1

这两个公式问题都很多，误差很大，公式1在 $P_0$ 是精确的，越往后误差越大，而公式2在 $P_n$ 是精确的，越往前误差越大。

因此Forrest提出的想法是，前半部分按第一个公式算，后半部分按第二个公式算，如下：

$\hat{P_i}=\left\{\begin{matrix} P_{i}^%&&i=0,1,...,(n-1)/2\\ P_i^*&&i=(n-1)/2+1,...,n-1 \end{matrix}\right.$

后面Farin提出一个想法，把这两个公式线性插值一下，如下：

$\hat{P_i}=(1-\frac{i}{n-i})P_i^%+\frac{i}{n-i}P_i^*$

到这基本就把贝塞尔曲线和它的性质，操作给介绍的差不多了。长须一口气，huuuuuuuuuuuuuuuuuuu~

逐段的贝塞尔曲线（Piecewise Bezier Curves）

我们看看贝塞尔曲线存在的一些问题，如下图一个十阶的贝塞尔曲线

这里会存在一些问题：

首先二阶三阶的贝塞尔曲线我们很容易通过控制点就想象出曲线的大致形状，但是当控制点很多的时候，我们很难想象出曲线大致的形状。
其次我们无法做到只修改曲线的某一部分，因为只要动一个控制点，整个曲线都会跟着发生变换。
高阶的贝塞尔曲线往往会导致拐来拐去的，导致并不光滑，但是例如飞机汽车的表面都是很光滑的。

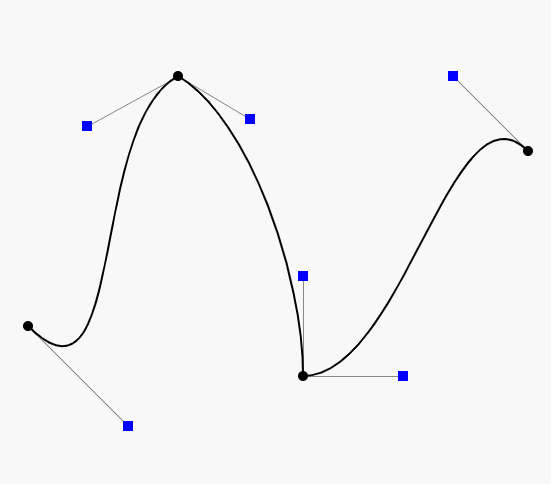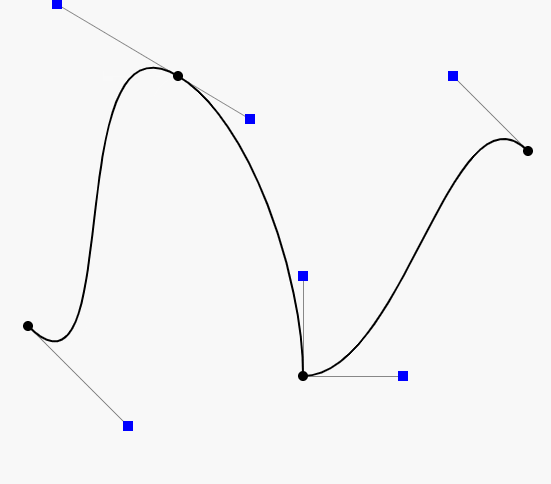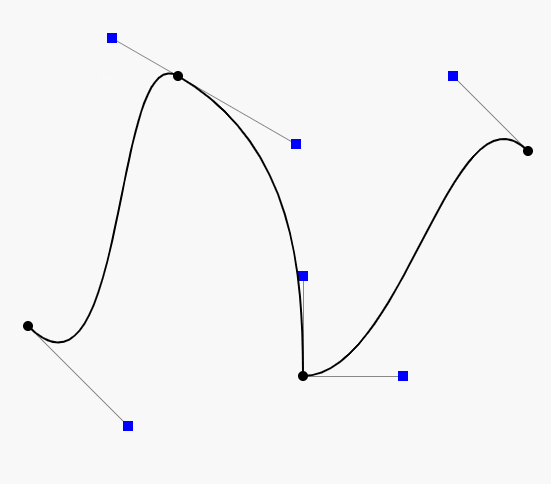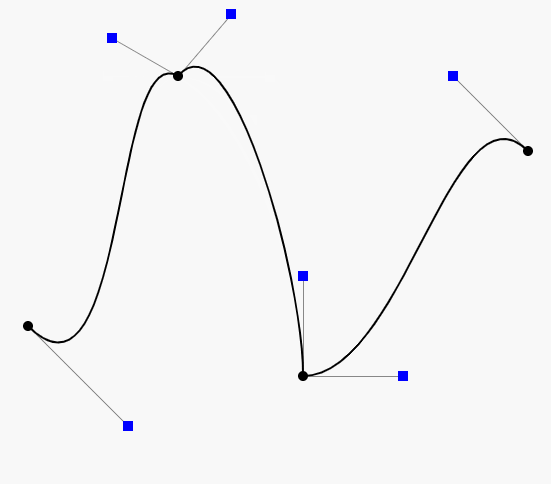
因此在CAD的应用中，通常不鼓励使用高阶的贝塞尔曲线，而是使用低阶贝塞尔曲线（通常用四阶的）相连，如下图：

如图，由三段四阶的贝塞尔曲线连成（是不是很像PS的钢笔工具），分别是ABCD，HIJK和WXYZ。

连续性

如上图，在K（或W）点有很明显的拐点，这种现象我们称之为不连续。在微积分的观念里，我们对曲线上的某一个点左右求导，如果导数相等，那么就是连续的，对于这种连续性我们称为传统的连续性。那么对应K（或W）点的左右导数根据贝塞尔曲线导数的性质我们很容易就得到 3(K-J) 和 3(w-x)，很明显是不相等的，所以不连续。

但是这里我们可以举一个反例，如下图：

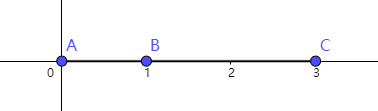
我们以AB两点作为控制点形成贝塞尔曲线，那么该曲线自然就是AB线段，同样的，我们以BC两点再形成一个贝塞尔曲线为BC线段，AB和BC形成一条直线段。此时B点左右的导数分别为(B-A)和(C-B)，这两个值明显是不相等的，按微积分里的定义就是不连续。可是它明明是一条直线，怎么会不连续呢？这个反例意味着传统的连续性不适用于描述CAD和图形学中形状的连续性，因此提出了几何连续性（Geometric continuity）的概念。

所谓几何连续性的概念，就是导数的方向一样，我们即可认为是连续的。对于例子中的直线，我们认为它是几何连续的，但是速度不一样，例如一个小蚂蚁在ABC上爬，在AB上较慢，在BC上变快了。

那么我们就有如下定义，假设我们有 $P_0,P_1,P_2...P_n$ 和 $Q_0,Q_1,Q_2...Q_n$ 形成的两条贝塞尔曲线，如果：