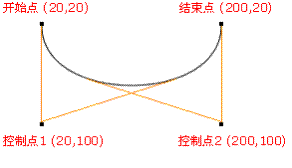
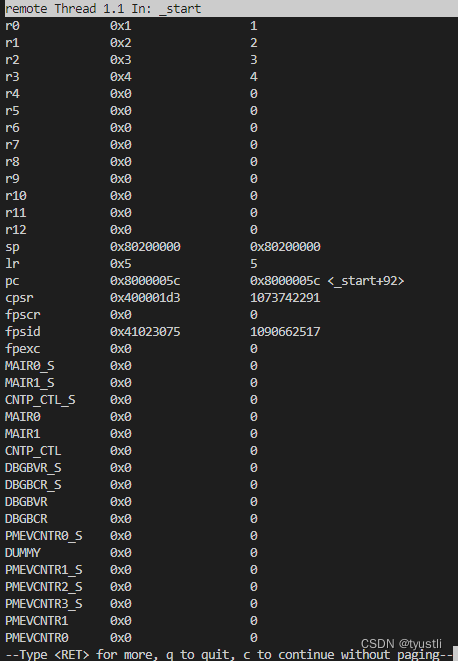
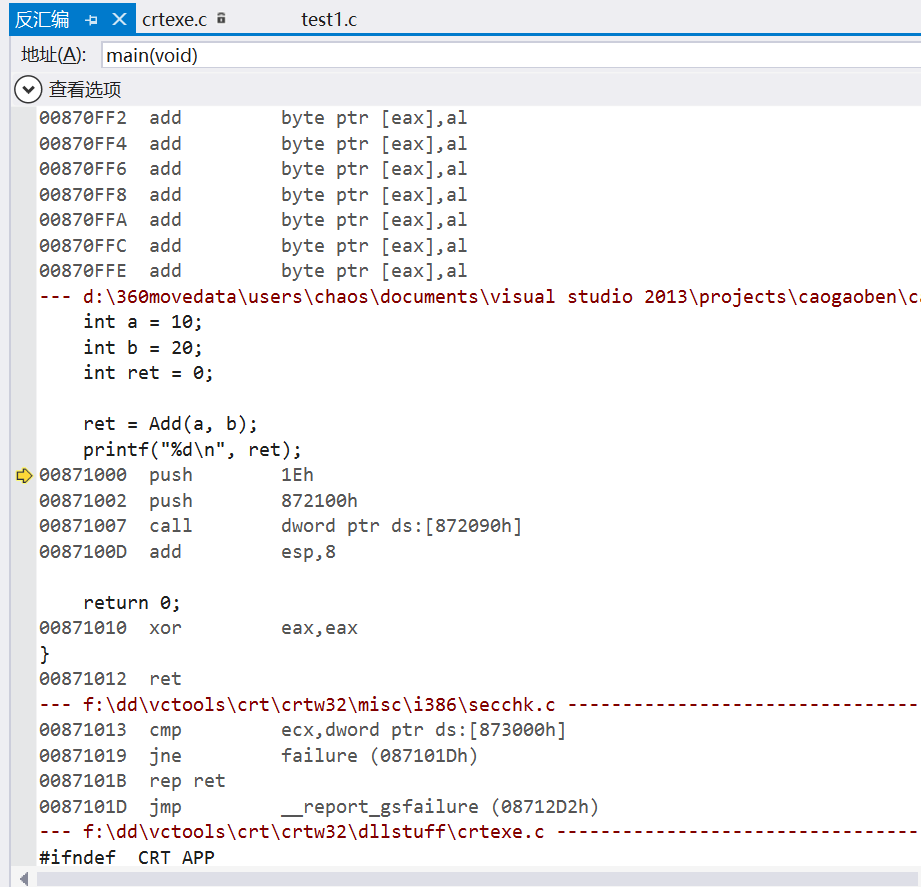
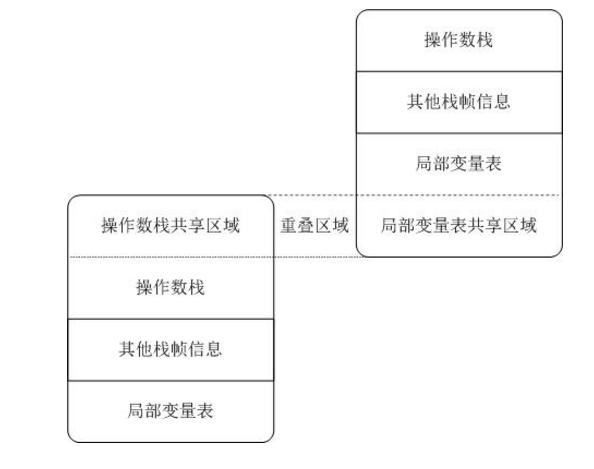
在绘制圆和圆弧一节中,了解到在Canvas中可以使用arc()和arcTo()绘制制圆或弧线,但很多时候,仅这两个方法还不能满足我们实际的需求,特别是绘制复杂的曲线。不过值得庆幸的是,在Canvas中还提供了其他的方法可以帮助我们绘制复杂的曲线。那就是我们今天要说的贝塞尔曲线,在Canvas中提供了两个独立的方法:quadraticCurveTo()和bezierCurveTo()方法。这两个方法就是贝塞尔曲线。
贝塞尔曲线
相信很多同学都知道“贝塞尔曲线”这个词,我们在很多地方都能经常看到。但是,可能并不是每位同学都清楚地知道,到底什么是“贝塞尔曲线”,又是什么特点让它有这么高的知名度。
贝塞尔曲线的数学基础是早在 1912 年就广为人知的伯恩斯坦多项式。但直到 1959 年,当时就职于雪铁龙的法国数学家 Paul de Casteljau 才开始对它进行图形化应用的尝试,并提出了一种数值稳定的 de Casteljau 算法。然而贝塞尔曲线的得名,却是由于 1962 年另一位就职于雷诺的法国工程师 Pierre Bézier 的广泛宣传。他使用这种只需要很少的控制点就能够生成复杂平滑曲线的方法,来辅助汽车车体的工业设计。
正是因为控制简便却具有极强的描述能力,贝塞尔曲线在工业设计领域迅速得到了广泛的应用。不仅如此,在计算机图形学领域,尤其是矢量图形学,贝塞尔曲线也占有重要的地位。今天我们最常见的一些矢量绘图软件,如 Flash、Illustrator、CorelDraw 等,无一例外都提供了绘制贝塞尔曲线的功能。甚至像 Photoshop 这样的位图编辑软件,也把贝塞尔曲线作为仅有的矢量绘制工具(钢笔工具)包含其中。
贝塞尔曲线在 web 开发领域同样占有一席之地。CSS3 新增了 transition-timing-function 属性,它的取值就可以设置为一个三次贝塞尔曲线方程。在此之前,也有不少 JavaScript 动画库使用贝塞尔曲线来实现美观逼真的缓动效果。
有关于贝塞尔曲线的详细介绍,可以查看维基百科的相关介绍。
贝塞尔曲线实例化
对于贝塞尔曲线,我们常看到的有:
线性贝塞尔曲线
二次方贝塞尔曲线
三次方贝塞尔曲线
n阶贝塞尔曲线
线性贝塞尔曲线
给定点P0、P1,线性贝塞尔曲线只是一条两点之间的直线,这条线由下面的公式可以计算出来:
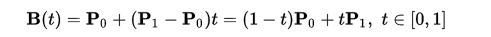
线性贝塞尔曲线函数中的t会经过由P0至P1的B(t)所描述的曲线。例如当t=0.25时,B(t)即一条由点P0至P1路径的四分之一处。就像由0至1的连续t,B(t)描述一条由P0至P1的直线。
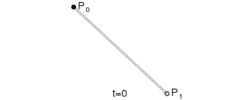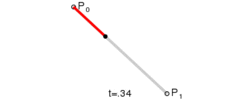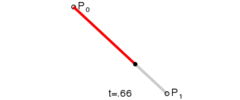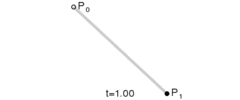
上图演示了:线性贝塞尔曲线演示动画,t在[0,1]区间,其实就是绘制了一条直线。
二次方贝塞尔曲线
二次方贝塞尔曲线的路径由给定点P0、P1、P2的函数B(t)追踪:
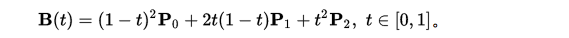
为建构二次贝塞尔曲线,可以中介点Q0和Q1作为由0至1的t:
由P0至P1的连续点Q0,描述一条线性贝塞尔曲线。
由P1至P2的连续点Q1,描述一条线性贝塞尔曲线。
由Q0至Q1的连续点B(t),描述一条二次贝塞尔曲线。