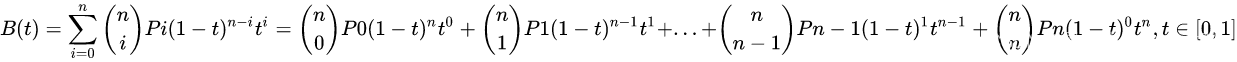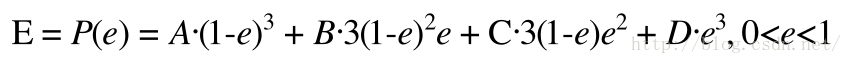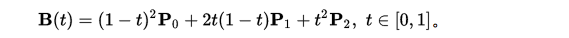浅谈贝塞尔曲线

前段时间做了一个手写板功能的东西，其中手写部分用二次贝塞尔曲线完成，今天就来总结一下贝塞尔曲线在Android中的应用，先简单介绍各阶贝塞尔曲线的原理，然后实现通过贝塞尔曲线实现波浪线功能，感兴趣的同学继续看下去吧！

概念

在数学的数值分析领域中，贝塞尔曲线（英语：Bézier curve，亦作“贝塞尔”）是计算机图形学中相当重要的参数曲线。更高维度的广泛化贝塞尔曲线就称作贝兹曲面，其中贝兹三角是一种特殊的实例。

贝塞尔曲线于1962年，由法国工程师皮埃尔·贝兹（Pierre Bézier）所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由保尔·德·卡斯特里奥于1959年运用德卡斯特里奥算法开发，以稳定数值的方法求出贝塞尔曲线。

贝塞尔曲线主要用于二维图形应用程序中的数学曲线，曲线由起始点，终止点（也称锚点）和控制点组成，通过调整控制点，通过一定方式绘制的贝塞尔曲线形状会发生变化。根据方程的最高阶数，又分为线性贝赛尔曲线，二阶贝塞尔曲线、三阶贝塞尔曲线和高阶贝塞尔曲线。

线性贝塞尔曲线

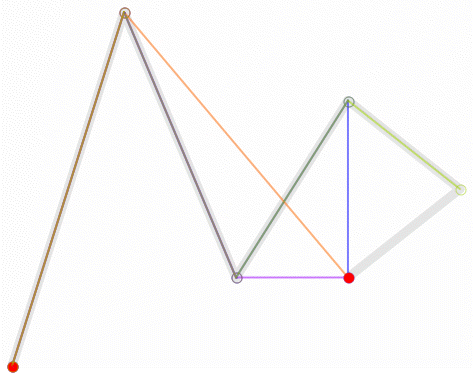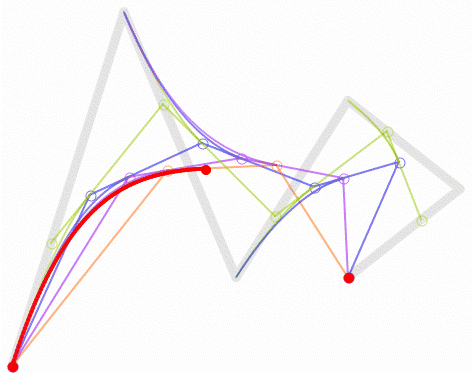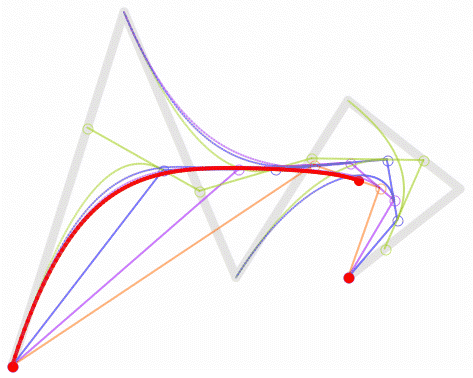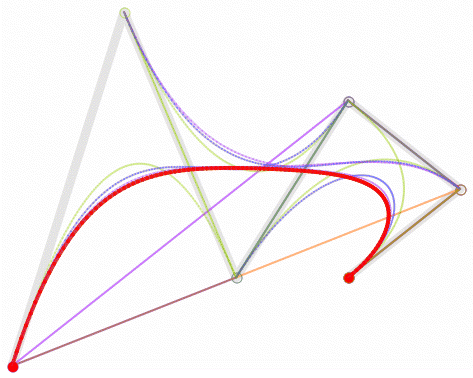
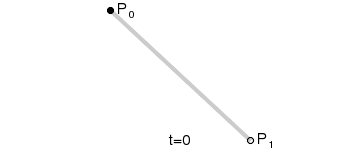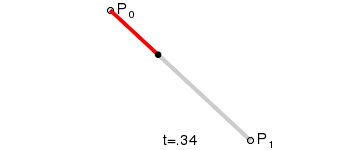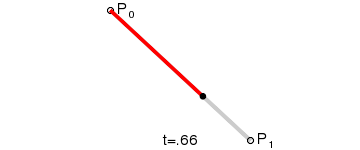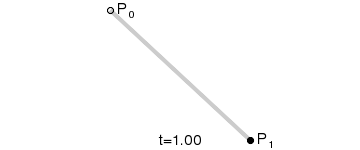
一阶贝塞尔曲线有两个点，一个是贝塞尔曲线的起点，一个是曲线的终点，主要就是画一条线段

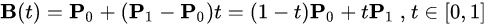
线性贝塞尔曲线函数中的t会经过由P0至P1的B（t）所描述的曲线。例如当t=0.25时，B（t）即一条由点P0至P1路径的四分之一处。就像由0至1的连续t，B（t）描述一条由P0至P1的直线。

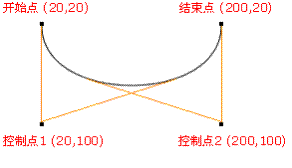
二阶贝塞尔曲线

二阶贝塞尔曲线有三个点，一个是贝塞尔曲线的起点，一个是曲线控制点，一个是曲线终点，主要就是用来画不是很复杂的曲线，例如上面说的手写板功能，使用的就是二阶贝塞尔曲线

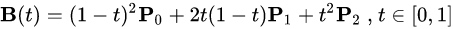
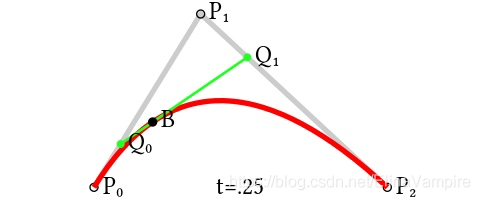
为建构二次贝塞尔曲线，可以中介点Q0和Q1作为由0至1的t：

由P0至P1的连续点Q0，描述一条线性贝塞尔曲线。
由P1至P2的连续点Q1，描述一条线性贝塞尔曲线。
由Q0至Q1的连续点B（t），描述一条二次贝塞尔曲线。

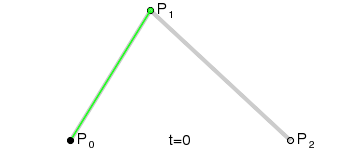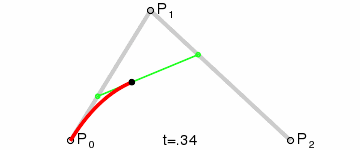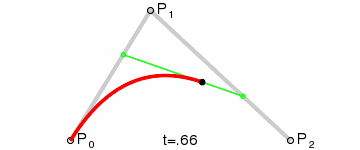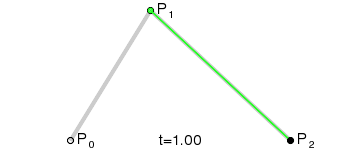
p0是起始点，p1是控制点，p2是终点

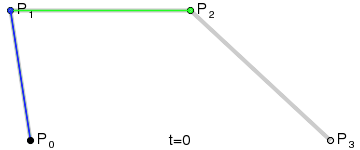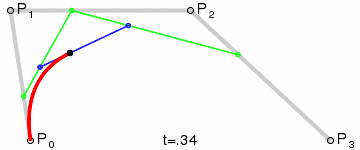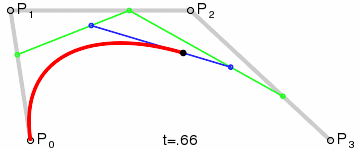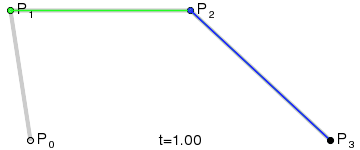
三阶贝塞尔曲线

P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝塞尔曲线。曲线起始于P0走向P1，并从P2的方向来到P3。一般不会经过P1或P2；这两个点只是在那里提供方向资讯。P0和P1之间的间距，决定了曲线在转而趋进P2之前，走向P1方向的“长度有多长”。

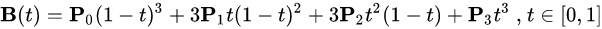
对于三次曲线，可由线性贝塞尔曲线描述的中介点Q0、Q1、Q2，和由二次曲线描述的点R0、R1所建构：

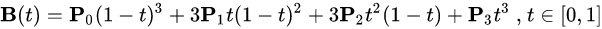
在这里插入图片描述

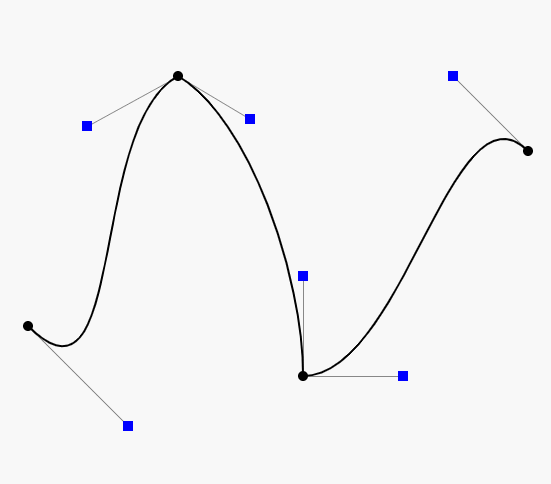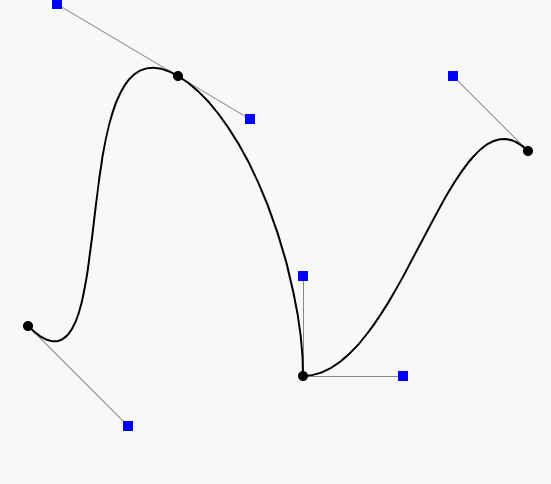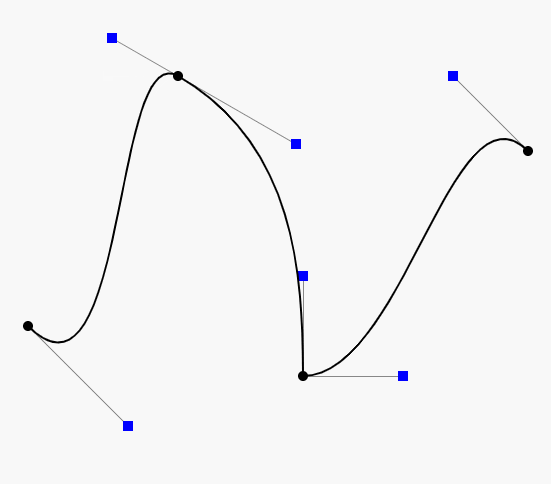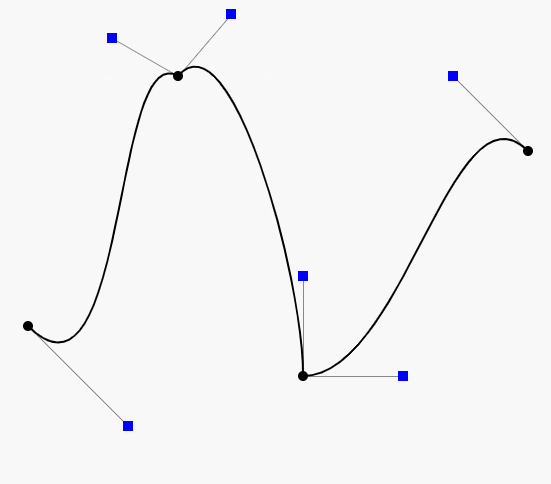
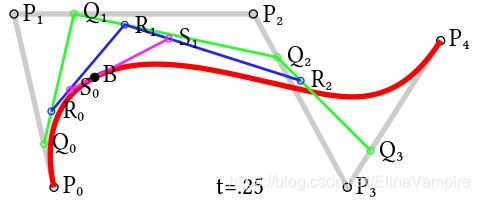
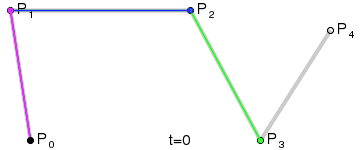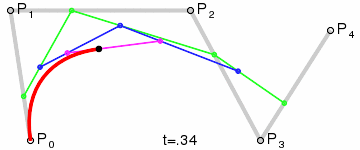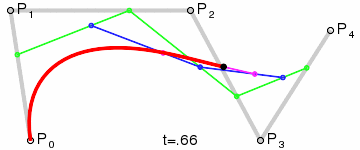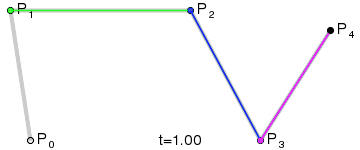
高阶贝塞尔曲线

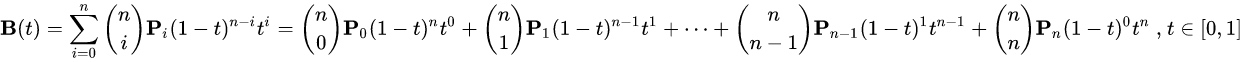
在这里插入图片描述

不管是几阶，原理都一样，感兴趣的可以自己证明一下这个原理，下面给出四阶的原理图
在这里插入图片描述

贝塞尔曲线在android中的应用

贝塞尔曲线在android中主要用于各种自定义view，主要是实现曲线更平滑，例如上面说的手写板，波浪线等等，在Android中用的最多的是二阶和三阶贝塞尔曲线，下面我们一起用二阶贝塞尔曲线写一个实例了解一下在Android中的用法，最后附上贝塞尔曲线实现水波纹效果

二阶贝塞尔曲线：

quadTo(x1,y1,x2,y2)

x1:控制点x坐标
y1:在控制点y坐标
x2：终点x坐标
y2:终点y坐标

rQuadTo(dx1,dy1,dx2,dy2)

dx1：控制点相对起点的x位移
dy1：控制点相对起点的y位移
dx2：终点相对起点的x位移
dy2：终点相对起点的y位移

在这里插入图片描述

public class SecondOrderBezierView extends View {Path mPath;Paint mPaint;Paint mLinePaint;float centerX, centerY;float mX, mY;float startX, startY;float endX, endY;public SecondOrderBezierView(Context context) {super(context);init();}public SecondOrderBezierView(Context context, AttributeSet attrs) {super(context, attrs);init();}void init() {mPaint = new Paint();mPaint.setAntiAlias(true);mPaint.setColor(Color.RED);mPaint.setStrokeWidth(10f);mPaint.setStyle(Paint.Style.STROKE);mLinePaint = new Paint();mLinePaint.setAntiAlias(true);mLinePaint.setColor(Color.GRAY);mLinePaint.setStrokeWidth(2f);mLinePaint.setStyle(Paint.Style.STROKE);mPath = new Path();}@Overrideprotected void onSizeChanged(int w, int h, int oldw, int oldh) {super.onSizeChanged(w, h, oldw, oldh);centerX = w/2;centerY = h/2;startX = centerX-250;startY = centerY;endX = centerX + 250;endY = centerY;mX = centerX;mY = centerY - 500;}@Overridepublic boolean onTouchEvent(MotionEvent event) {switch (event.getAction()) {case MotionEvent.ACTION_DOWN:case MotionEvent.ACTION_MOVE:mX = event.getX();mY = event.getY();break;}invalidate();return true;}@Overrideprotected void onDraw(Canvas canvas) {super.onDraw(canvas);mPath.reset();mPath.moveTo(startX, startY);mPath.quadTo(mX, mY, endX, endY);canvas.drawPath(mPath, mPaint);canvas.drawLine(startX, startY, mX, mY, mLinePaint);canvas.drawLine(mX, mY, endX, endY, mLinePaint);}
}

三阶贝塞尔曲线

cubicTo(float x1, float y1, float x2, float y2,float x3, float y3)

x1, y1控制点1的坐标
x2, y2控制点2的坐标
x2, y2终点的坐标

rCubicTo(float x1, float y1, float x2, float y2,float x3, float y3)

x1, y1控制点1相对于起点的位置
x2, y2控制点2相对于起点的位置
x2, y2终点相对于起点的位置

实例省略，跟二阶贝塞尔曲线差不多，多了一个控制点

学习了贝塞尔曲线，下面来实际操作一下

一起实现波浪效果，首先先画出基本的波浪形状，起点，控制点，终点确定之后先画出一段的波浪线，再修改起点，终点，控制点画第二段波浪线

mPath.moveTo(startX, startY);
mPath.quadTo(mX, mY, centerX, centerY);
mPath.quadTo(centerX * 3 / 2, centerY + 300, endX, endY);

然后通过修改Paint的Style为FILL_AND_STROKE，通过path的lineto把下面部分填充

mPaint.setStyle(Paint.Style.FILL_AND_STROKE);mPath.lineTo(2 * centerX, 2 * centerY);
mPath.lineTo(0, 2 * centerY);

在这里插入图片描述

最后通过动画让波浪动起来, 说明由于使用的平移动画，所以需要在屏幕外多画一个完整的波浪线

demo仅供参考，当然也可以通过其他方式实现

public class WaveView extends View {Paint mPaint;Path mPath;float mX, mY, centerX, centerY, startX, startY, endX, endY;int waveCount, waveLength, mOffsetX;ValueAnimator mValueAnimator;public WaveView(Context context) {super(context);init();}public WaveView(Context context, AttributeSet attrs) {super(context, attrs);init();}private void init() {mPaint = new Paint();mPaint.setAntiAlias(true);mPaint.setStyle(Paint.Style.STROKE);mPaint.setStyle(Paint.Style.FILL_AND_STROKE);mPaint.setStrokeWidth(10f);mPaint.setColor(Color.RED);mPath = new Path();waveLength = 800;startWave();}@Overrideprotected void onSizeChanged(int w, int h, int oldw, int oldh) {super.onSizeChanged(w, h, oldw, oldh);waveLength = w;centerX = w / 2;centerY = h / 2;startX = 0;startY = centerY;endX = w;endY = centerY;mX = centerX / 2;mY = centerY - 300;waveCount = (int) Math.round(w / waveLength + 1.5);}@Overrideprotected void onDraw(Canvas canvas) {super.onDraw(canvas);mPath.reset();mPath.moveTo(-waveLength + mOffsetX, centerY);for (int i = 0; i < waveCount; i++) {mPath.rQuadTo(waveLength / 4, -100, waveLength / 2, 0);mPath.rQuadTo(waveLength / 4, +100, waveLength / 2, 0);}mPath.lineTo(2 * centerX, 2 * centerY);mPath.lineTo(0, 2 * centerY);mPath.close();canvas.drawPath(mPath, mPaint);}void startWave() {mValueAnimator = ValueAnimator.ofInt(0, waveLength);mValueAnimator.setDuration(1000);mValueAnimator.setRepeatCount(ValueAnimator.INFINITE);mValueAnimator.setInterpolator(new LinearInterpolator());mValueAnimator.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {@Overridepublic void onAnimationUpdate(ValueAnimator valueAnimator) {mOffsetX = (int) valueAnimator.getAnimatedValue();invalidate();}});mValueAnimator.start();}
}