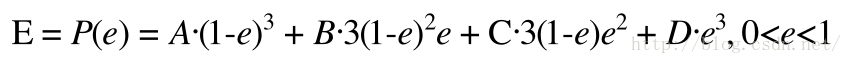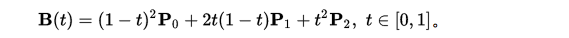贝塞尔曲线工具类

article/2025/10/18 19:33:49

贝塞尔曲线工具类

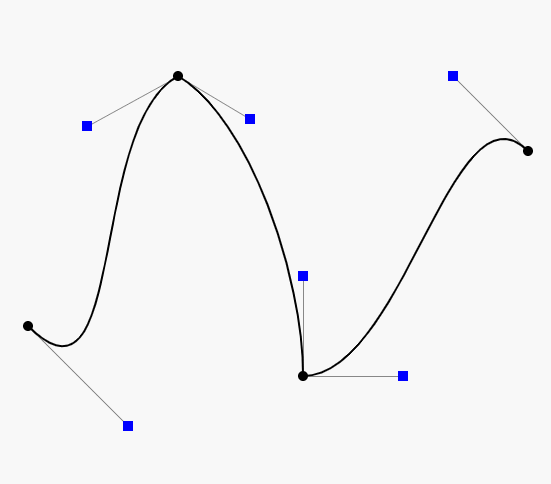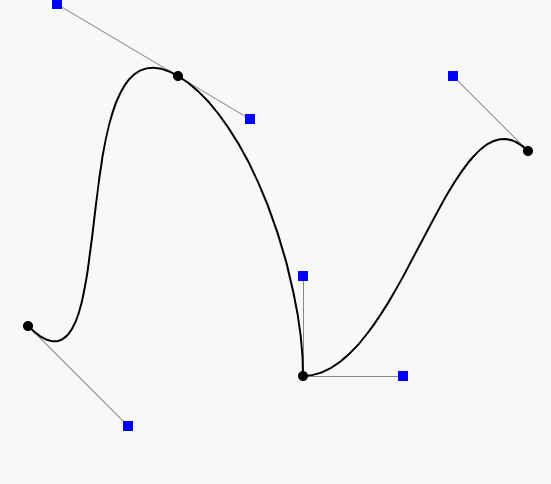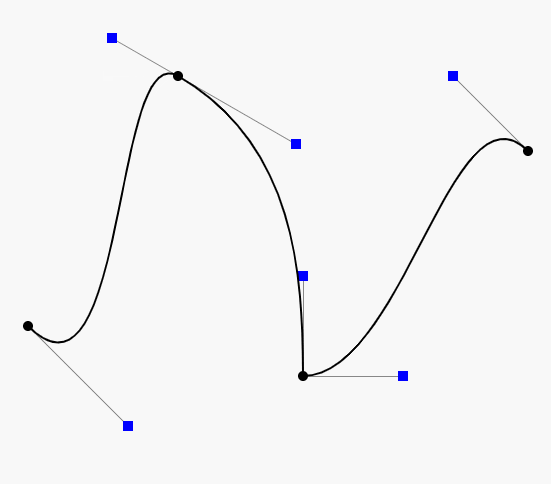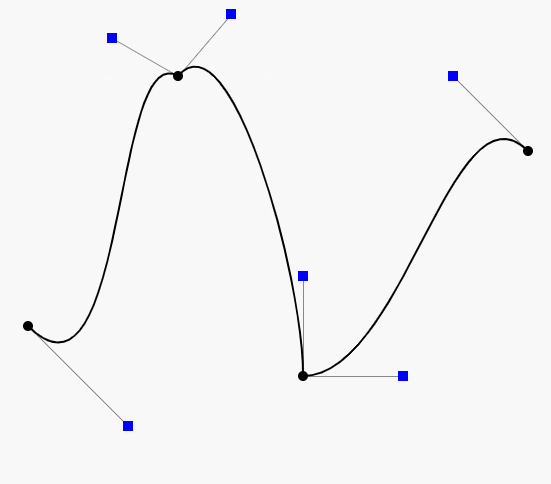
先上一张效果图看效果
在这里插入图片描述

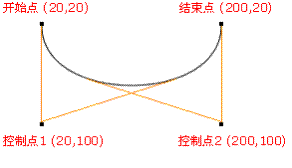
贝塞尔曲线

用于计算N阶贝塞尔曲线上的点，根据传入控制点的个数判定阶数N
贝塞尔曲线计算公式:
在这里插入图片描述

工具类源码

public class BezierUtils {/*** 获取二项式系数** @param l 行(杨辉三角)* @param c 列(杨辉三角)* @return 系数*/private static int getBinomialCoefficient(@IntRange(from = 0) int l, @IntRange(from = 0) int c) {int lotteryOdds = 1;for (int i = 1; i <= c; i++)lotteryOdds = lotteryOdds * (l - i + 1) / i;return lotteryOdds;}/*** 获取贝塞尔曲线上t位置的点** @param t      变化值* @param points 控制点* @return 当前t对应的点*/public static PointF getBezierPoint(@FloatRange(from = 0, to = 1) float t, List<PointF> points) {if (points == null || points.size() < 2)return null;PointF result = new PointF();int n = points.size() - 1;//N阶for (int i = 0; i <= n; i++) {int binomialCoefficient = getBinomialCoefficient(n, i);double v = Math.pow(1 - t, n - i) * Math.pow(t, i);result.x += binomialCoefficient * (points.get(i).x * v);result.y += binomialCoefficient * (points.get(i).y * v);}return result;}/*** 获取贝塞尔曲线上t位置的点** @param t      变化值* @param points 控制点* @return 当前t对应的点*/public static PointF getBezierPoint(@FloatRange(from = 0, to = 1) float t, PointF... points) {if (points == null || points.length < 2)return null;return getBezierPoint(t, Arrays.asList(points));}/*** 获取贝塞尔曲线路径** @param precision  生成路径分段的精度* @param points 控制点* @return 贝塞尔曲线路径*/public static Path getBezierPath(@IntRange(from = 1) int precision, List<PointF> points) {if (precision < 1 || points == null || points.size() < 2)return null;float division = 1f / precision;float t = division;PointF lastP = points.get(0);Path path = new Path();path.moveTo(lastP.x, lastP.y);while (t < 1) {PointF point = getBezierPoint(t, points);path.lineTo(point.x, point.y);t += division;}PointF endP = points.get(points.size() - 1);path.lineTo(endP.x, endP.y);return path;}/*** 获取贝塞尔曲线路径** @param precision  生成路径分段的精度* @param points 控制点* @return 贝塞尔曲线路径*/public static Path getBezierPath(@IntRange(from = 1) int precision, PointF... points) {if (precision < 1 || points == null || points.length < 2)return null;return getBezierPath(precision, Arrays.asList(points));}
}

示例代码

public class MyView extends View {private PointF f1;private PointF f2;private PointF f3;private PointF f4;private Paint paint;private Paint paint2;private Paint paint3;private Path path1;private Path path2;private Path path3;private PointF point;private PointF point1;private PointF point2;public MyView(Context context) {this(context, null);}public MyView(Context context, @Nullable AttributeSet attrs) {this(context, attrs, 0);}public MyView(Context context, @Nullable AttributeSet attrs, int defStyleAttr) {super(context, attrs, defStyleAttr);paint = new Paint();paint.setStrokeWidth(20);paint.setColor(Color.RED);paint.setAntiAlias(true);paint.setDither(true);paint2 = new Paint();paint2.setStrokeWidth(10);paint2.setColor(Color.BLUE);paint2.setStyle(Paint.Style.STROKE);paint2.setAntiAlias(true);paint2.setDither(true);paint3 = new Paint();paint3.setStrokeWidth(15);paint3.setColor(Color.YELLOW);paint3.setAntiAlias(true);paint3.setDither(true);path1 = new Path();path2 = new Path();path3 = new Path();}@Overrideprotected void onSizeChanged(int w, int h, int oldw, int oldh) {super.onSizeChanged(w, h, oldw, oldh);int measuredHeight = getMeasuredHeight();int measuredWidth = getMeasuredWidth();f1 = new PointF(measuredWidth / 3, measuredHeight / 3);f2 = new PointF(measuredWidth / 3, measuredHeight / 3 * 2);f3 = new PointF(measuredWidth / 3 * 2, measuredHeight / 3);f4 = new PointF(measuredWidth / 3 * 2, measuredHeight / 3 * 2);}@Overrideprotected void onDraw(Canvas canvas) {super.onDraw(canvas);//画四个控制点(图中黑色的四个点)canvas.drawPoint(f1.x, f1.y, paint);canvas.drawPoint(f2.x, f2.y, paint);canvas.drawPoint(f3.x, f3.y, paint);canvas.drawPoint(f4.x, f4.y, paint);//系统API画3阶贝塞尔曲线(图中蓝色线条)path1.moveTo(f1.x, f1.y);path1.cubicTo(f1.x, f1.y, f2.x, f2.y, f3.x, f3.y);paint2.setColor(Color.BLUE);canvas.drawPath(path1, paint2);//系统API画3阶贝塞尔曲线(图中绿色线条)path2.moveTo(f1.x, f1.y);path2.cubicTo(f2.x, f2.y, f3.x, f3.y, f4.x, f4.y);paint2.setColor(Color.GREEN);canvas.drawPath(path2, paint2);//系统API画2阶贝塞尔曲线(图中灰色线条)path3.moveTo(f1.x, f1.y);paint2.setColor(Color.LTGRAY);path3.quadTo(f2.x, f2.y, f4.x, f4.y);canvas.drawPath(path3, paint2);//画图中三个黄色变动的点(取自灰色线条)if (point != null) {canvas.drawPoint(point.x, point.y, paint3);}//画图中三个黄色变动的点(取自蓝色线条)if (point1 != null) {canvas.drawPoint(point1.x, point1.y, paint3);}//画图中三个黄色变动的点(取自绿色线条)if (point2 != null) {canvas.drawPoint(point2.x, point2.y, paint3);}}//画图中三个黄色变动的点(取自灰色线条)public void drawPoint(@FloatRange(from = 0, to = 1) float t) {point = BezierUtils.getBezierPoint(t, f1, f2, f4);invalidate();}//画图中三个黄色变动的点(取自绿色线条)public void drawPoint2(@FloatRange(from = 0, to = 1) float t) {point2 = BezierUtils.getBezierPoint(t, f1, f2, f3, f4);invalidate();}//画图中三个黄色变动的点(取自蓝色线条)public void drawPoint1(@FloatRange(from = 0, to = 1) float t) {point1 = BezierUtils.getBezierPoint(t, f1, f1, f2, f3);invalidate();}
}