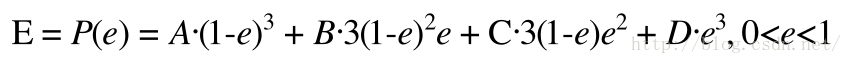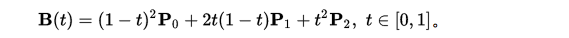1. 前言

贝塞尔曲线(Bézier curve)，又称贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线，贝兹曲线由线段与节点组成，节点是可拖动的支点，线段像可伸缩的皮筋，我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。

2. 介绍

2.1 一阶贝济埃曲线

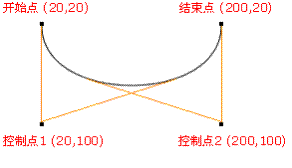
一阶贝济埃曲线的公式如下：

 B(t)=(1-t)P_0+tP_1，t属于0-1

P0为起始点，P1为终点，t 表示当前时间，B(t)表示公式的结果值。其实也就是一条从P0到P1的直线上，匀速运动的点值。

2.2 二阶贝塞尔曲线

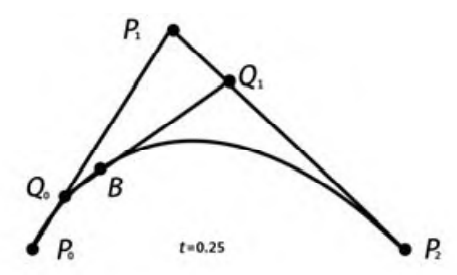
这条曲线的构成也就是每个t时刻，Q0和Q1的所属的直线的的t时刻的距离的点，这里也就是B。不妨将上面这个图简单标注下：

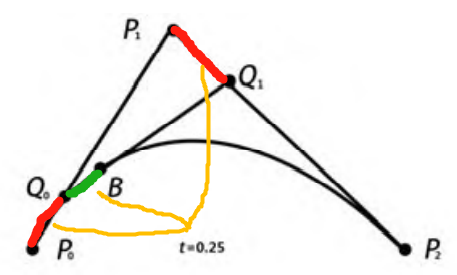
也就是在从P0到P1，进行匀速运动，在t=0.25的时刻走到Q0，类似的，从P1到P2经过匀速运动，在t=0.25的时刻走到Q1，对于Q0到Q1，经过匀速运动，在t=0.25的时刻走到B。而B也就是二阶贝塞尔曲线上的点。

2.3 三阶贝塞尔曲线

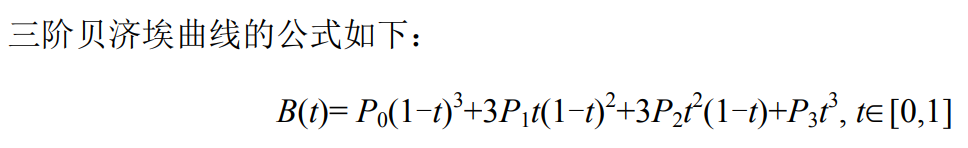
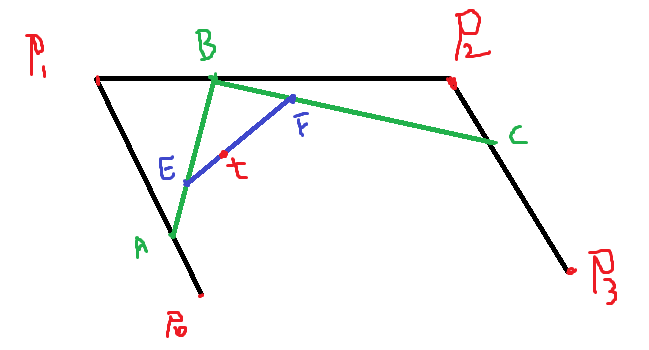
也就是说此时有两个控制点，对应着也就是三根连着的线段，类似的我们可以得到最终的t点：

那么，根据上面的规则，我们可以自己来实现一下贝赛尔曲线的计算方式，并将曲线绘制出来。

3. 一、二、三阶贝塞尔曲线实现

定义为：

class Point(var x: Float, var y: Float){
}/*** 得到贝赛尔曲线上的点集* @param points 起始、控制和终止点坐标* @param number 需要计算的贝赛尔曲线上的点的个数* @return 返回路径*/
private fun getBezierPointsPath(points: Array<Point>, number: Int): Path{val path = Path()for (time in 0 until number){val t = time * 1f / numberval point = calcPoint(points, t)if(time == 0){path.moveTo(point.x, point.y)} else {path.lineTo(point.x, point.y)}Log.e("TAG", "getBezierPointsPath: ${point.x} , ${point.y}", )}return path
}/*** 计算在t时刻上，位于贝赛尔曲线上的点的坐标* @param points 点的集合* @param t 时刻，属于0-1* @return 点坐标 Point*/
private fun calcPoint(points: Array<Point>, t: Float): Point{// 分别求任意两个点之间的在t时刻运动的距离// 任意两点，按照顺序分别为始和终var index = 0var len = points.size - 1while (index < len){points[index].x = getValueByTime(points[index].x, points[index + 1].x, t)points[index].y = getValueByTime(points[index].y, points[index + 1].y, t)index++if(index == len){index = 0len--}}return points[0]
}/*** 定义匀速运动的计算坐标* @param start 开始的位置* @param end 结束的位置* @param time 运动的时间，范围0-1* @return time时刻的运动位置*/
private fun getValueByTime(start: Float, end: Float, time: Float): Float{return start + (end - start) * time
}

然后使用：

// 绘图方法
override fun onDraw(canvas: Canvas?) {super.onDraw(canvas)canvas?.apply {val points = arrayOf(Point(200f, 400f), Point(100f, 20f), Point(500f, 20f), Point(800f, 400f))val numberOfPoint = 100mPath = getBezierPointsPath(points, numberOfPoint)drawPath(mPath, mPaint)}
}

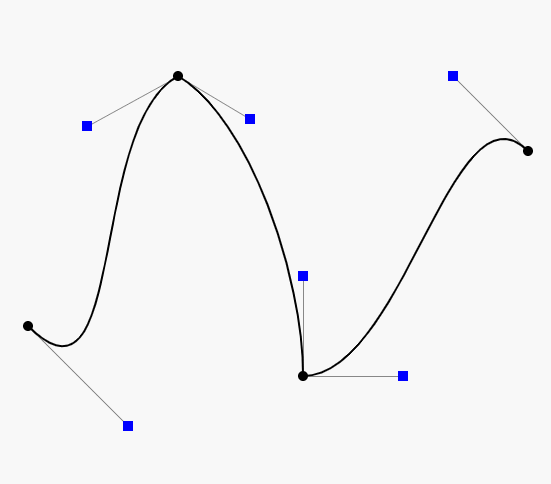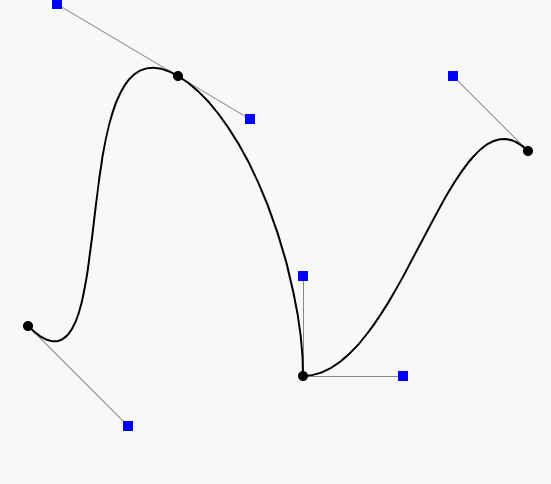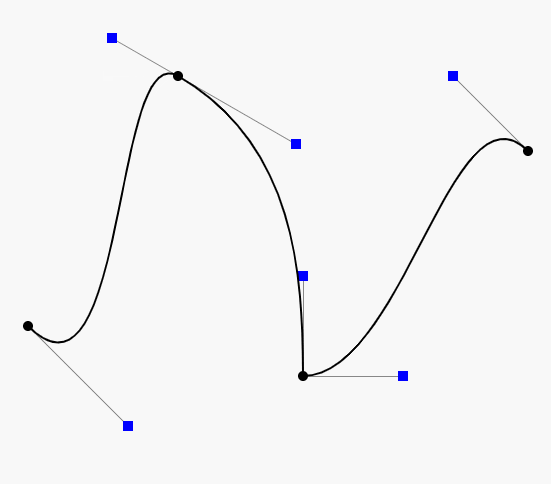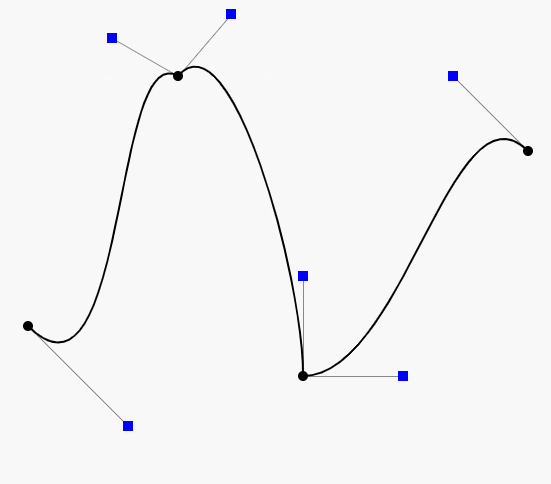
很明显，这里细粒度不够。可以把numberOfPoint 设置的更大些。当设置为1000的时候：

当然这里可以使用arrayOf的时候添加更多的点，以做到更加高阶的贝塞尔曲线，比如简单修改一下：

val points = arrayOf(Point(200f, 400f),Point(100f, 20f),Point(500f, 20f),Point(800f, 400f),Point(1000f, 20f)
)

也就是对应三个控制点，对应四阶本塞尔曲线，对应效果：

当然，在系统中其实也提供了一、二、三阶的贝赛尔曲线的API，所以通常直接调用即可。对应的如下：

• mPath.lineTo：进行直线绘制 ；
• mPath.quadTo(x1, y1, x2, y2) ：生成二次贝塞尔曲线，(x1,y1) 为控制点，(x2,y2)为结束点 ；
• mPath.cubicTo(x1, y1, x2, y2, x3, y3)：生成三次贝塞尔曲线， (x1,y1) 为控制点，(x2,y2)为控制点，(x3,y3) 为结束点；

4. 案例

/*** 学习波浪效果，其实也就是移动类似于正弦的连续图像，带来的视觉效果* @author 梦否* 2022年3月15日*/
class WaterRippleView : View {constructor(context: Context?) : super(context) {init()}constructor(context: Context?, attrs: AttributeSet?) : super(context, attrs) {init()}constructor(context: Context?, attrs: AttributeSet?, defStyleAttr: Int) : super(context,attrs,defStyleAttr) {init()}private lateinit var mPath: Pathprivate lateinit var mPaint: Paintprivate lateinit var points1: Array<MyPoint>private lateinit var points2: Array<MyPoint>class MyPoint(var x: Float, var y: Float)/*** 初始化方法*/private fun init() {mPath = Path()mPaint = Paint()mPaint.isDither = truemPaint.isAntiAlias = truemPaint.strokeWidth = 5fmPaint.color = Color.GRAYmPaint.style = Paint.Style.FILLval viewWidth = resources.displayMetrics.widthPixelspoints1 = arrayOf(MyPoint(0f * viewWidth, 200f),MyPoint(.33f * viewWidth, 20f),MyPoint(.66f * viewWidth, 360f),MyPoint(1f * viewWidth, 200f))points2 = arrayOf(MyPoint(-1f * viewWidth, 200f),MyPoint(-.66f * viewWidth, 20f),MyPoint(-.33f * viewWidth, 360f),MyPoint(0f * viewWidth, 200f),)// 三阶贝塞尔曲线，传入0，也就是初始时刻updatePathByDistance(0f)}override fun onDraw(canvas: Canvas?) {super.onDraw(canvas)canvas?.apply {drawPath(mPath, mPaint)}}/*** 根据距离来进行更新在贝赛尔曲线中的点的坐标值* @param distance 传入的距离*/private fun updatePathByDistance(distance: Float) {// 重置mPath.reset()// 设置mPath.moveTo(points2[0].x, points2[0].y)mPath.cubicTo(points2[1].x + distance,points2[1].y,points2[2].x + distance,points2[2].y,points2[3].x + distance,points2[3].y)mPath.cubicTo(points1[1].x + distance,points1[1].y,points1[2].x + distance,points1[2].y,points1[3].x + distance,points1[3].y)val y = resources.displayMetrics.heightPixelsmPath.lineTo(points1[3].x, y.toFloat())mPath.lineTo(points2[0].x + distance,  y.toFloat())mPath.lineTo(points2[0].x + distance, points2[0].y)}/*** 一直移动绘制的两个类似于正弦函数的路径*/var startedMove = falseprivate fun startMove() {startedMove = trueval animator = ValueAnimator.ofFloat(0f, resources.displayMetrics.widthPixels.toFloat())animator.duration = 800// 线性插值器，使之匀速运动animator.interpolator = LinearInterpolator()// 循环animator.repeatCount = ValueAnimator.INFINITEanimator.addUpdateListener(object : ValueAnimator.AnimatorUpdateListener {override fun onAnimationUpdate(animation: ValueAnimator?) {val value = animator.getAnimatedValue()updatePathByDistance(value as Float)// 重绘invalidate()}})animator.start()}override fun onTouchEvent(event: MotionEvent?): Boolean {super.onTouchEvent(event)var flag = falsewhen (event?.action) {MotionEvent.ACTION_DOWN -> {flag = trueif(!startedMove) startMove()}MotionEvent.ACTION_MOVE,MotionEvent.ACTION_UP -> {flag = false}}return flag}override fun onMeasure(widthMeasureSpec: Int, heightMeasureSpec: Int) {super.onMeasure(widthMeasureSpec, heightMeasureSpec)val minHeight = dp2px(300)val minWidth = dp2px(500)val widthSize = getMeasureSize(widthMeasureSpec, minWidth.toInt())val heightSize = getMeasureSize(heightMeasureSpec, minHeight.toInt())setMeasuredDimension(widthSize, heightSize)}/*** 计算高度和宽度*/private fun getMeasureSize(Spec: Int, minValue: Int): Int {var result = 0// 获取模式val mode = MeasureSpec.getMode(Spec)val size = MeasureSpec.getSize(Spec)// 判断一下when (mode) {MeasureSpec.AT_MOST -> {result = Math.min(size, minValue)}MeasureSpec.UNSPECIFIED -> {result = minValue}MeasureSpec.EXACTLY -> {result = size}}return result}/*** dp转换为px*/private fun dp2px(size: Int): Float {return resources.displayMetrics.density * size}
}

5. 后记

当然关于贝赛尔曲线的应用远不止如此。比如：Android开发之贝塞尔曲线进阶篇（仿直播送礼物，饿了么购物车动画），感兴趣的可以查阅原文。