【Unity3d游戏开发】游戏中的贝塞尔曲线以及其在Unity中的实现

article/2025/10/18 19:35:18

　　RT，马三最近在参与一款足球游戏的开发，其中涉及到足球的各种运动轨迹和路径，比如射门的轨迹，高吊球，香蕉球的轨迹。最早的版本中马三是使用物理引擎加力的方式实现的足球各种运动，后来的版本中使用了根据物理学公式手动计算位置和物体速度的方式实现，现在这个版本中使用的是DoTween+贝塞尔曲线调节来实现。（关于它们之间的各种优缺点我们会在以后单独开一篇博客来探讨，届时也会放出源代码互相学习下）好了，言归正传，今天马三就来和大家一起学习一下游戏中的贝塞尔曲线以及其在Unity中如何实现。

一、简介

贝塞尔曲线是最基本的曲线，一般用在计算机图形学和图像处理。贝塞尔曲线可以用来创建平滑的曲线的道路、弯曲的路径就像祖玛游戏、弯曲型的河流等。

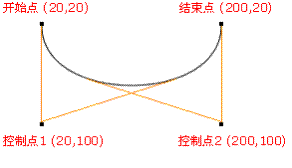
一条贝塞尔曲线是由一组定义的控制点 P0到 Pn，在 n 调用它的顺序 (n = 1 为线性，2 为二次，等.)。第一个和最后一个控制点总是具有终结点的曲线;然而，中间两个控制点 (如果有的话) 一般不会位于曲线上。

　　（1）贝塞尔曲线包含两个控制点即 n = 2 称为线性的贝塞尔曲线

　　（2）贝塞尔曲线包含三个控制点即 n = 3 称为二次贝塞尔曲线

　　（3）贝塞尔曲线包含四个控制点即 n = 4，所以称为三次贝塞尔曲线。

　　贝塞尔曲线返回点的贝塞尔函数，使用线性插值的概念作为基础。

二、公式

1.线性贝塞尔公式：

给定点P0、P1，线性贝兹曲线只是一条两点之间的直线。这条线由下式给出：

其等同于线性插值。

效果图（文章中部分图片转载自CSDN）：

2.二次贝塞尔公式：

二次方贝兹曲线的路径由给定点P0、P1、P2控制，这条线由下式给出：

效果图：

3.三次贝塞尔方程：

P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝兹曲线。曲线起始于P0走向P1，并从P2的方向来到P3。一般不会经过P1或P2；这两个点只是用来充当控制点。P0和P1之间的间距，决定了曲线在转而趋进P3之前，走向P2方向的“长度有多长”。

曲线的参数形式为：

效果图：

4.一般参数形式的贝塞尔方程：

N阶贝兹曲线可如下推断。给定点P0、P1、…、Pn，其贝兹曲线即：

如上公式可如下递归表达：用表示由点 P0、 P1、…、 Pn所决定的贝兹曲线。

TIPS:

通过两个低阶的贝塞尔曲线插值的堆叠总能够获得更高阶的贝塞尔曲线，通俗的来说通过对两条低阶的贝塞尔曲线插值，你可以求得一条高一阶的贝塞尔曲线。

比如：二次贝塞尔曲线是点对点的两个线性贝塞尔曲线的线性插值，三次贝塞尔曲线是两条二次贝塞尔曲线的线性插值。

三、实现与应用

效果图：

通过调节起始点（左边的白球）、控制点（中间的白球）和结束点（右边的白球）可以获得到不同的贝塞尔曲线，然后使用LineRender组件将路径绘制出来，以方便观察。下面就是实现此功能的代码：

 1 using UnityEngine;
 2 using System.Collections.Generic;
 3 [RequireComponent(typeof(LineRenderer))]
 4 public class Bezier : MonoBehaviour
 5 {
 6     public Transform[] controlPoints;
 7     public LineRenderer lineRenderer;
 8  
 9     private int layerOrder = 0;
10     private int _segmentNum = 50;
11  
12  
13     void Start()
14     {
15         if (!lineRenderer)
16         {
17             lineRenderer = GetComponent<LineRenderer>();
18         }
19         lineRenderer.sortingLayerID = layerOrder;
20     }
21  
22     void Update()
23     {
24  
25         DrawCurve();
26  
27     }
28  
29     void DrawCurve()
30     {
31             for (int i = 1; i <= _segmentNum; i++)
32             {
33                 float t = i / (float)_segmentNum;
34                 int nodeIndex = 0;
35                 Vector3 pixel = CalculateCubicBezierPoint(t, controlPoints[nodeIndex].position,
36                     controlPoints[nodeIndex+1].position, controlPoints[nodeIndex+2].position);
37                 lineRenderer.numPositions = i;
38                 lineRenderer.SetPosition(i - 1, pixel);
39             }
40  
41     }
42  
43     Vector3 CalculateCubicBezierPoint(float t, Vector3 p0, Vector3 p1, Vector3 p2)
44     {
45         float u = 1 - t;
46         float tt = t * t;
47         float uu = u * u;
48  
49         Vector3 p = uu * p0;
50         p += 2 * u * t * p1;
51         p += tt * p2;
52  
53         return p;
54     }
55      
56 }

CalculateCubicBezierPoint()函数负责根据T值计算出对应的贝塞尔曲线中的点，DrawCurve()函数通过不断的改变T值，并调用CalculateCubicBezierPoint()获得坐标点，然后通过LineRenderer将这些点绘制出来。

为了使用方便，可以将计算贝赛尔曲线的方法放到一个工具类中——BezierUtils类：

 1 using System.Collections;
 2 using System.Collections.Generic;
 3 using UnityEngine;
 4  
 5 public class BezierUtils
 6 {
 7     /// <summary>
 8     /// 根据T值，计算贝塞尔曲线上面相对应的点
 9     /// </summary>
10     /// <param name="t"></param>T值
11     /// <param name="p0"></param>起始点
12     /// <param name="p1"></param>控制点
13     /// <param name="p2"></param>目标点
14     /// <returns></returns>根据T值计算出来的贝赛尔曲线点
15     private static  Vector3 CalculateCubicBezierPoint(float t, Vector3 p0, Vector3 p1, Vector3 p2)
16     {
17         float u = 1 - t;
18         float tt = t * t;
19         float uu = u * u;
20  
21         Vector3 p = uu * p0;
22         p += 2 * u * t * p1;
23         p += tt * p2;
24  
25         return p;
26     }
27  
28     /// <summary>
29     /// 获取存储贝塞尔曲线点的数组
30     /// </summary>
31     /// <param name="startPoint"></param>起始点
32     /// <param name="controlPoint"></param>控制点
33     /// <param name="endPoint"></param>目标点
34     /// <param name="segmentNum"></param>采样点的数量
35     /// <returns></returns>存储贝塞尔曲线点的数组
36     public static Vector3 [] GetBeizerList(Vector3 startPoint, Vector3 controlPoint, Vector3 endPoint,int segmentNum)
37     {
38         Vector3 [] path = new Vector3[segmentNum];
39         for (int i = 1; i <= segmentNum; i++)
40         {
41             float t = i / (float)segmentNum;
42             Vector3 pixel = CalculateCubicBezierPoint(t, startPoint,
43                 controlPoint, endPoint);
44             path[i - 1] = pixel;
45             Debug.Log(path[i-1]);
46         }
47         return path;
48  
49     }
50 }