一、贝塞尔曲线的概念 
        对于两点之间的连线，我们可以用直线进行连接效果如下：

        其中的每一个F点都在AB连接的线段上。

        这就是一阶贝塞尔曲线。

       

 如果我们加入一个控制点C，那么做图如下：

 

       1、连接AC,BC；

        2、在AC,BC上找到 AD/AC = CE/CB 的点D,E；

        3、连接DE，在DE上寻找点F，F点需要满足：EF/ ED = AD/AC = CE/CB；

        4、找出所有F点，连接而成的线，就是贝塞尔曲线；

       两个线段根据等比关系找点的贝塞尔曲线，一般也称为二阶贝塞尔曲线。

       关于贝赛尔曲线的基本数学理论大概就是上面的内容。

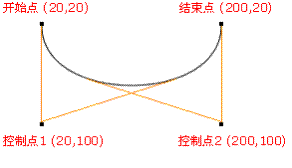
       除了二阶贝塞尔曲线外还有三阶，四阶贝塞尔曲线，它们的控制点依次增加，我们常用的是三阶贝塞尔曲线，有两个控制点，控制点决定着生成完成后曲线的形状。

      三阶贝塞尔曲线的绘制示意图如下：

 

     1、首先连接AC,AB,BD；

     2、找到EFG三点，满足 AE/AC = BF/BA = DG/DB；

     3、连接EF.FG；

     4、找到J，I两点，满足 AE/AC = BF/BA = DG/DB = FJ/FE = GI/GF；

     5、连接JI两点；

     6、找到H点，满足AE/AC = BF/BA = DG/DB = FJ/FE = GI/GF = IH/IJ；

     7、F点从A移动到B,所计算出的H点连成的线，就是三阶贝塞尔曲线；

二、三阶贝塞尔曲线控制点的计算方法
        介绍完了什么是贝塞尔曲线，现在来说遇到的问题：

        现在已知有A,B.C.D,E,F,G,H点若干个，假如它们直线连接如下

 

       可以看出，连接直线并不平滑，在连接点上会出现方向突变。

       如果想要生成光滑曲线，需要进行控制点计算，计算出A,B,C,D,E,F,H各个带你的控制点进行计算

       每个位置要计算出左右两个控制点L1,L2：

算法如下：

1、两端的控制点位置为自己本身，例如A点控制点位置L1=L2=A ，G点 L1=L2=G；

2、中间控制点的位置由左右两个点的位置决定，例如C点的控制点位置通过计算BCD连接而成的三角形决定；

3、计算向量和 与三角形BCD的夹角 ；

4、计算垂直于三角形BCD所在平面的单位向量，计算方法为的向量积，再归一化；

5、向量绕轴旋转 （ - ）/ 2 度 得到向量；

6、向量绕轴旋转 -（ - ）/ 2 度得到向量 ；

7、将5,6计算结果乘以一个比例因子的到向量CL1 与CL2（的大小决定曲线的形状，一般设置在0.5以下）；

8、L1坐标 = CL1 + C ， L2坐标 = CL2 + C；

    注：如果为180度，那么跳过4，5，6步的计算

————————————————

原文链接：https://blog.csdn.net/q943520218/article/details/103827268