多目标跟踪之数据关联算法——匈牙利算法

article/2025/10/6 23:54:08

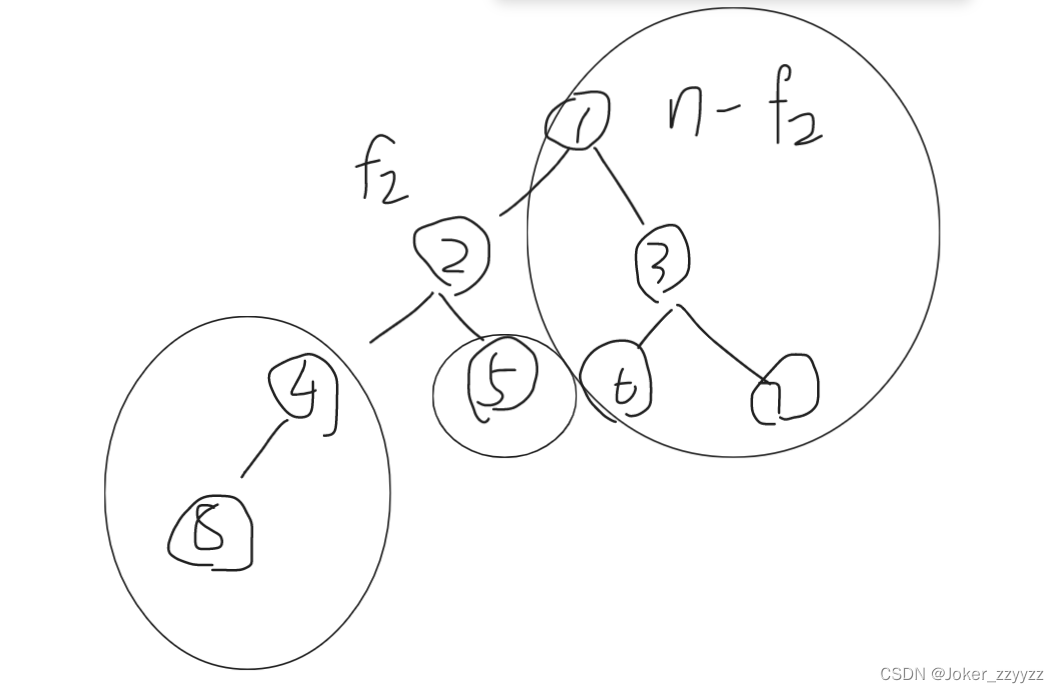
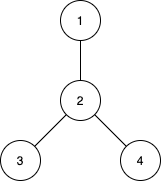
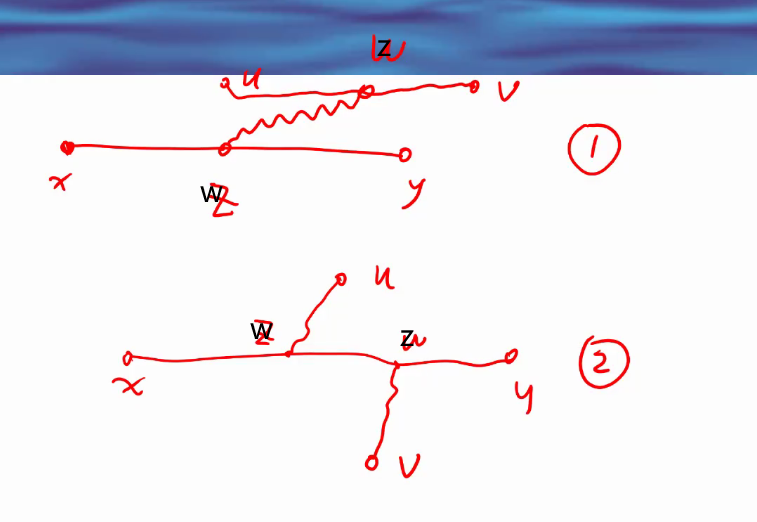
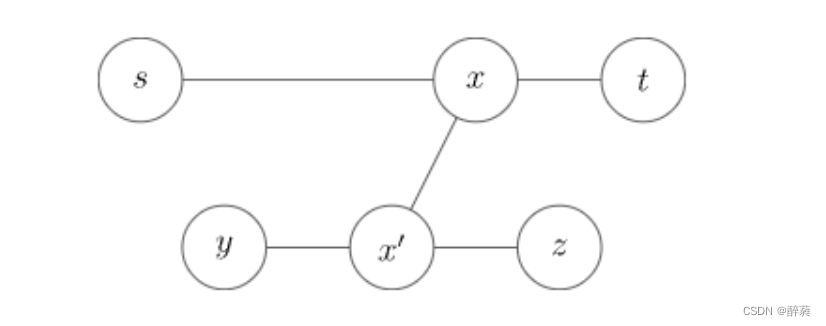
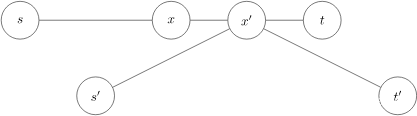
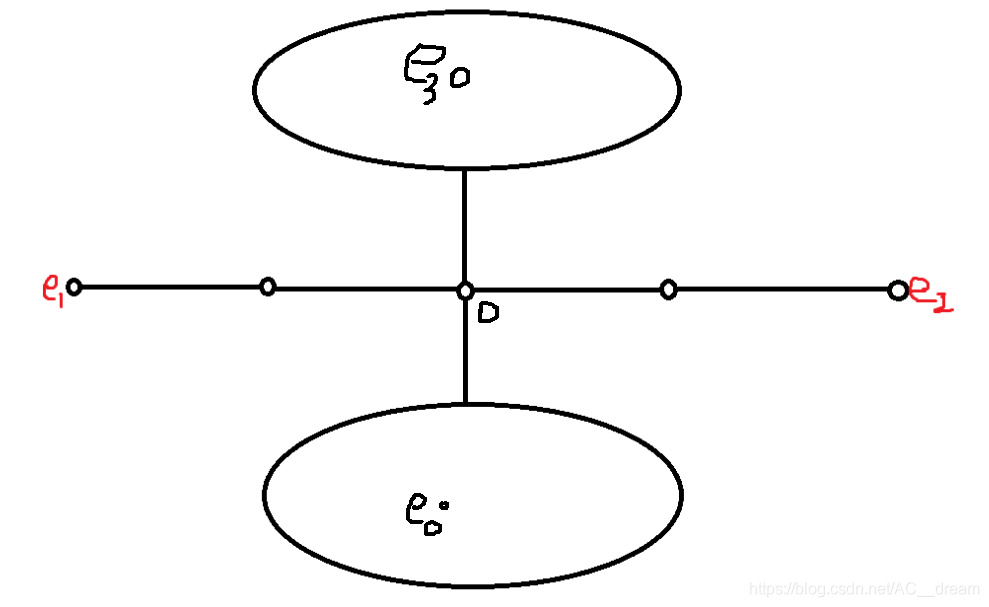
零、Track和Detection的cost matrix，distance metric。距离计算的方式有如下几种：

  1.  距离cost distance metric，track和detection的距离矩阵。
    外观距离appearance distance，来自检测切片ROI的网络特征提取；——余弦距离
    运动模型距离 马氏距离，来自检测-跟踪的kalman校正距离，马氏距离==二维高斯分布，利用相关可以去除维度间的量纲影响，并考虑维度间的相关性。比如x,y,a,h四者的相关性和量纲差异，可以不被考虑。
  2. 距离矩阵的分配算法——匈牙利算法Hungarian，这里指的是Kuhn&Munkres Hungarian， KM匈牙利算法（加权的匈牙利算法）
    ① KM匈牙利，n个轨迹，m个检测。padding方式为max(n,m)
    ② KM匈牙利，直接对矩形n×m进行分配，不进行任何形式的padding
    ③ KM匈牙利，padding方式为(n+m)*(n+m)，主对角有数值。其余分别为inf和0
    这些算法的优缺点和差异分别为什么？
  3. 距离矩阵进入匈牙利算法可以有不同的padding形式，他们对分配结果的差异是怎样的？

track_t CTrack::CalcDistCenter(const CRegion& reg) const
{Point_t diff = m_predictionPoint - reg.m_rrect.center;return sqrtf(sqr(diff.x) + sqr(diff.y));
}track_t CTrack::CalcDistRect(const CRegion& reg) const
{std::array<track_t, 5> diff;diff[0] = reg.m_rrect.center.x - m_lastRegion.m_rrect.center.x;diff[1] = reg.m_rrect.center.y - m_lastRegion.m_rrect.center.y;diff[2] = static_cast<track_t>(m_lastRegion.m_rrect.size.width - reg.m_rrect.size.width);diff[3] = static_cast<track_t>(m_lastRegion.m_rrect.size.height - reg.m_rrect.size.height);diff[4] = static_cast<track_t>(m_lastRegion.m_rrect.angle - reg.m_rrect.angle);track_t dist = 0;for (size_t i = 0; i < diff.size(); ++i){dist += sqr(diff[i]);}return sqrtf(dist);
}track_t CTrack::CalcDistJaccard(const CRegion& reg) const
{track_t intArea = static_cast<track_t>((reg.m_brect & m_lastRegion.m_brect).area());track_t unionArea = static_cast<track_t>(reg.m_brect.area() + m_lastRegion.m_brect.area() - intArea) + 1e-6;return std::fabs(1 - intArea / unionArea);
}
track_t CTrack::CalcDistHist(const RegionEmbedding& embedding) const
{track_t res = 1;if (!embedding.m_hist.empty() && !m_regionEmbedding.m_hist.empty()){
#if (((CV_VERSION_MAJOR == 4) && (CV_VERSION_MINOR < 1)) || (CV_VERSION_MAJOR == 3))res = static_cast<track_t>(cv::compareHist(embedding.m_hist, m_regionEmbedding.m_hist, CV_COMP_BHATTACHARYYA));//res = 1.f - static_cast<track_t>(cv::compareHist(hist, m_regionEmbedding.m_hist, CV_COMP_CORREL));
#elseres = static_cast<track_t>(cv::compareHist(embedding.m_hist, m_regionEmbedding.m_hist, cv::HISTCMP_BHATTACHARYYA));
#endif}else{assert(0);CV_Assert(!embedding.m_hist.empty());CV_Assert(!m_regionEmbedding.m_hist.empty());}return res;
}
track_t CTrack::CalcMahalanobisDist(const cv::RotatedRect& rrect) const
{cv::Mat res1, predictPoint;// res1 = Hn * Pn+1|n+1 * Hn^T + Rn+1	error covariance// res2 = Hn * Xn+1|nm_kalman.GetPtStateAndResCov(res1, predictPoint);double mahaDist = 0.0;if (!res1.empty() && !predictPoint.empty()){cv::Mat icovar_Pn;cv::invert(res1, icovar_Pn, cv::DECOMP_SVD);cv::Mat measurePoint;if (predictPoint.rows == 2)			// PointUpdatemeasurePoint = (cv::Mat_<track_t>(2, 1) << rrect.center.x, rrect.center.y); // detectionelsemeasurePoint = (cv::Mat_<track_t>(4, 1) << rrect.center.x, rrect.center.y, rrect.size.width, rrect.size.height); // predictmahaDist = cv::Mahalanobis(measurePoint, predictPoint, icovar_Pn);mahaDist += std::log(cv::determinant(res1));}return static_cast<track_t>(mahaDist);
}
std::pair<track_t, bool> CTrack::CalcCosine(const RegionEmbedding& embedding) const
{track_t res = 1;if (!embedding.m_embedding.empty() && !m_regionEmbedding.m_embedding.empty()){double xy = embedding.m_embedding.dot(m_regionEmbedding.m_embedding);double norm = sqrt(embedding.m_embDot * m_regionEmbedding.m_embDot) + 1e-6;
#if 0res = 1.f - 0.5f * fabs(static_cast<float>(xy / norm));
#elseres = 0.5f * static_cast<float>(1.0 - xy / norm);
#endif//std::cout << "CTrack::CalcCosine: " << embedding.m_embedding.size() << " - " << m_regionEmbedding.m_embedding.size() << " = " << res << std::endl;return { res, true };}else{//assert(0);//CV_Assert(!embedding.m_embedding.empty());//CV_Assert(!m_regionEmbedding.m_embedding.empty());return { 0, false };}
}

 一、匈牙利算法维基百科：https://zh.wikipedia.org/wiki/匈牙利算法

  • 匈牙利算法最早是由匈牙利数学家Dénes Kőnig康尼格和Jenő Egerváry用来求矩阵中0元素的个数的一种方法。由此他证明『矩阵中独立0元素的最多个数等于能覆盖cover所有0元素的最少直线数』
  • 匈牙利算法是一种在多项式时间内求解任务分配问题的组合优化算法，并推动了后来的原始对偶方法。
  • 1955年，美国数学家哈罗德·库恩W.W.Kuhn（库恩）Harold W. Kuhn在求解著名的指派问题时引用了这一结论，并对具体算法做了改进，仍然称为匈牙利算法。此算法之所以被称作匈牙利算法，是因为算法很大一部分是基于以前匈牙利数学家Dénes Kőnig和Jenő Egerváry的工作之上创建起来的。[1][2]
  • 1957年，詹姆士·芒克勒斯Munkres在1957年回顾了该算法，并发现它的时间复杂度为（强）多项式时间。[3] 此后该算法被称为Kuhn–Munkres算法或Munkres分配算法。原始算法的时间复杂度为 O(n^{4})，但杰克·爱德蒙斯与卡普发现可以修改算法达到 O(n^{3})运行时间，富泽也独立发现了这一点。L·R·福特和D·R·福尔克森将该方法推广到了一般运输问题。2006年发现卡尔·雅可比 Jacobis bound在19世纪就解决了指派问题，该解法在他死后在1890年以拉丁文发表。[4]

参考书目

  • R.E. Burkard, M. Dell'Amico, S. Martello: Assignment Problems (Revised reprint). SIAM, Philadelphia (PA.) 2012. ISBN 978-1-61197-222-1
  • M. Fischetti, "Lezioni di Ricerca Operativa", Edizioni Libreria Progetto Padova, Italia, 1995.
  • R. Ahuja, T. Magnanti, J. Orlin, "Network Flows", Prentice Hall, 1993.
  • S. Martello, "Jeno Egerváry: from the origins of the Hungarian algorithm to satellite communication". Central European Journal of Operations Research 18, 47–58, 2010

参考文献

  1. ^ Harold W. Kuhn, "The Hungarian Method for the assignment problem", Naval Research Logistics Quarterly, 2: 83–97, 1955. Kuhn's original publication.
  2. ^ Harold W. Kuhn, "Variants of the Hungarian method for assignment problems", Naval Research Logistics Quarterly, 3: 253–258, 1956.
     https://econweb.ucsd.edu/~v2crawford/hungar.pdf  Kuhn的paper1960年9月29日。
  3. ^ J. Munkres, "Algorithms for the Assignment and Transportation Problems", Journal of the Society for Industrial and Applied Mathematics, 5(1):32–38, 1957 March.
  4. ^ JACOBI'S BOUND

外部链接

  • Bruff, Derek, "The Assignment Problem and the Hungarian Method", [1] （页面存档备份，存于互联网档案馆）
  • Mordecai J. Golin, Bipartite Matching and the Hungarian Method, Course Notes, Hong Kong University of Science and Technology.
  • R. A. Pilgrim, Munkres' Assignment Algorithm. Modified for Rectangular Matrices （页面存档备份，存于互联网档案馆）, Course notes, Murray State University.
  • Mike Dawes, The Optimal Assignment Problem, Course notes, University of Western Ontario.
  • On Kuhn's Hungarian Method – A tribute from Hungary, András Frank, Egervary Research Group, Pazmany P. setany 1/C, H1117, Budapest, Hungary.
  • Lecture: Fundamentals of Operations Research - Assignment Problem - Hungarian Algorithm, Prof. G. Srinivasan, Department of Management Studies, IIT Madras.
  • Extension: Assignment sensitivity analysis (with O(n^4) time complexity), Liu, Shell.
  • Solve any Assignment Problem online, provides a step by step explanation of the Hungarian Algorithm.

各种语言的算法实现链接

（请注意，并非所有这些都满足 O(n^{3}) 时间约束。） 

  • C implementation with O ( n 3 )  time complexityO(n^{3})
  • Java implementation of O ( n 3 ) time variantO(n^{3})
  • Python implementation (see also here)
  • Ruby implementation with unit tests
  • C# implementation
  • D implementation with unit tests (port of the Java O ( n 3 )  version)O(n^{3})
  • Online interactive implementation Please note that this implements a variant of the algorithm as described above.
  • Graphical implementation with options (Java applet)
  • Serial and parallel implementations.
  • Implementation in Matlab and C
  • Perl implementation
  • Lisp implementation
  • C++ (STL) implementation (multi-functional bipartite graph version)
  • C++ implementation
  • C++ implementation of the O ( n 3 )  algorithmO(n^{3})C++ implementation of the O ( n 3 )  algorithm (BSD

http://chatgpt.dhexx.cn/article/q2gww3yp.shtml

相关文章

EAST算法简单解析

EAST算法简单解析

前言 最近写了很多算法代码的解析&#xff0c;但是却很少写原理的解析&#xff0c;这段时间学得快忘得也快&#xff0c;所以寻思这几天写几篇学过算法的原理&#xff0c;可能不是很详细但是一定很简单&#xff0c;利于理解。 算法介绍 EAST: An Efficient and Accurate Scen…
阅读更多...
定位算法初探

定位算法初探

定位算法初探 一、指纹定位算法介绍 指纹定位(finger-printing localization)算法&#xff0c;是基于室内环境复杂&#xff0c;信号反射折射所形成的在不同位置形成的不同的信号强度信息而提出的一套算法。 指纹算法能很好的利用了反射折射所形成的信号信息&#xff0c;离线首…
阅读更多...
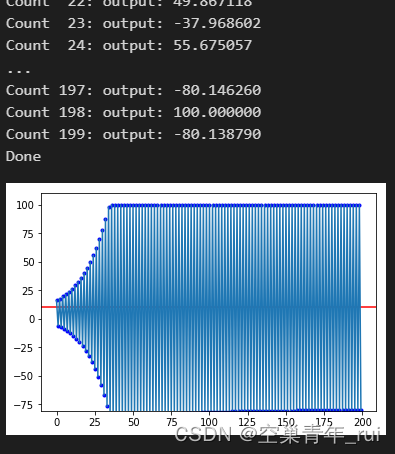
使用python模拟实现PID控制算法

使用python模拟实现PID控制算法

使用python模拟实现PID控制算法 PID控制算法是工业应用中最广泛算法之一&#xff0c;在闭环系统的控制中&#xff0c;可自动对控制系统进行准确且迅速的校正。 P、I、D分别是“比例&#xff08;proportional&#xff09;、积分&#xff08;integral&#xff09;、微分&#xff…
阅读更多...
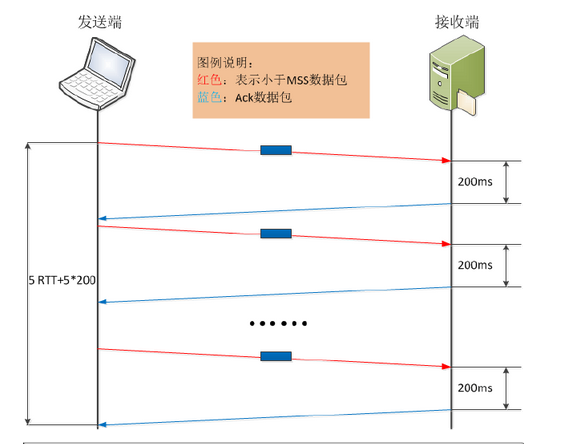
TCP Nagle算法简述

TCP Nagle算法简述

TCP/IP协议中&#xff0c;无论发送多少数据&#xff0c;总是要在数据前面加上协议头&#xff0c;同时&#xff0c;对方接收到数据&#xff0c;也需要发送ACK表示确认。为了尽可能的利用网络带宽&#xff0c;TCP总是希望尽可能的发送足够大的数据。 &#xff08;一个连接会设置M…
阅读更多...
倒角算法推导

倒角算法推导

推导原理基本很简单&#xff1a; 已知AB&#xff0c; BC两条线段&#xff0c;且交于B点&#xff0c;求倒角半径为 L&#xff0c;AB&#xff0c;BC的倒角 以最短边&#xff08;假定为AB&#xff09;长 LAB&#xff0c; 在BC中&#xff0c;以B为起点&#xff0c;找出与LAB同长度…
阅读更多...
[控制算法]

[控制算法]

[常用控制算法] 0.博览众长 0.1 视频 1. DR_CAN b站 0.2 文章 1.控制算法整理 0.3 传统 VS 现代控制算法 1. 传统 传统控制算法&#xff1a;PID&#xff0c;模糊&#xff0c;神经网络控制算法。 2. 现代 现代控制算法有比例&#xff0c;LQR算法(用于线性系统)&#x…
阅读更多...
求树的直径证明

求树的直径证明

树的直径&#xff08;最长路&#xff09; 的详细证明 主要是利用了反证法&#xff1a; 假设 s-t这条路径为树的直径&#xff0c;或者称为树上的最长路 现有结论&#xff0c;从任意一点u出发搜到的最远的点一定是s、t中的一点&#xff0c;然后在从这个最远点开始搜&#xff0c;就…
阅读更多...
树的直径和树的重心

树的直径和树的重心

1.树包括有根树和无根树&#xff0c;有根树是有向图的子图&#xff0c;无根树是无向图的子图&#xff0c;都满足边数等于节点数减一。根是入度为零或没有父亲的节点 2.树的直径&#xff1a;树上最长的简单路径&#xff08;不重复经过点的路径&#xff09; 3.求解算法&#xf…
阅读更多...
树的直径总结

树的直径总结

树的直径 一、定义 在一棵树中&#xff0c;最远的两个子节点之间的距离被称为树的直径&#xff1b; 链接这两个点的路径被称为树的最长链&#xff1b; 有两种求法&#xff0c;时间复杂度均为 O ( n ) O(n) O(n) &#xff1b; 二、树形DP 1. 状态 由于一个点的最长路通过…
阅读更多...
基础算法 - 树的直径

基础算法 - 树的直径

题目地址&#xff1a;https://leetcode-cn.com/problems/tree-diameter/ 1245. 树的直径 难度中等48收藏分享切换为英文接收动态反馈 给你这棵「无向树」&#xff0c;请你测算并返回它的「直径」&#xff1a;这棵树上最长简单路径的 边数。 我们用一个由所有「边」组成的数…
阅读更多...
树的直径-c++

树的直径-c++

题目 实验室里原先有一台电脑(编号为1)&#xff0c;最近氪金带师咕咕东又为实验室购置了N-1台电脑&#xff0c;编号为2到N。每台电脑都用网线连接到一台先前安装的电脑上。但是咕咕东担心网速太慢&#xff0c;他希望知道第i台电脑到其他电脑的最大网线长度&#xff0c;但是可怜…
阅读更多...
求树的直径算法以及证明

求树的直径算法以及证明

以下为两次dfs&#xff08;bfs&#xff09;的做法以及正确性证明。 算法步骤 &#xff08;1&#xff09;任取树上一点S&#xff0c;以S为源点BFS得S到各个顶点的d值&#xff1b; &#xff08;2&#xff09;取d值最大者之一为P&#xff0c;再以P为源点BFS得P到各个顶点的d值&am…
阅读更多...
求树的直径

求树的直径

树的直径&#xff0c;即树上的最长路径&#xff0c;显然&#xff0c;树的直径可以有很多条&#xff08;考虑一棵菊花&#xff09;。 接下来我们考虑如何求出一棵树的直径。有很多种O(n)的算法。 算法1&#xff1a;我们任取树中的一个节点x&#xff0c;找出距离它最远的点y&am…
阅读更多...
数据结构 树的直径

数据结构 树的直径

学习的最大理由是想摆脱平庸&#xff0c;早一天就多一份人生的精彩&#xff1b;迟一天就多一天平庸的困扰。 学习日记 目录 学习日记 一、定义 二、两次DFS 定理&#xff1a; 反证法证明&#xff1a; 1、若y在d(t,s)上 2、若y不在d(s,t)上&#xff0c;且d(y,z)与d(s.t)…
阅读更多...
树的直径（最长的简单路径）

树的直径（最长的简单路径）

题解&#xff1a;分析一下&#xff0c;由于是树&#xff0c;所以两点之间的路径有且只有一条&#xff0c;为了求出欧拉路&#xff0c;所以必然会向回走&#xff0c;从递归的角度来看&#xff0c;假设x看作一个树根&#xff0c;有t个孩子y1…yt。其中每个孩子为根的子树欧拉路都…
阅读更多...
树的直径概念及求解

树的直径概念及求解

文章目录 1. 使用两次DFS求得树的直径2. 使用树形DP求得树的直径3. 性质4. 参考文献和习题 树上任意两节点之间最长的简单路径即为树的「直径」。显然&#xff0c;一棵树可以有多条直径&#xff0c;他们的长度相等。可以用两次 D F S / B F S DFS/BFS DFS/BFS 或者树形 D P D…
阅读更多...
树的直径两种求法

树的直径两种求法

首先先介绍一下什么是树的直径&#xff0c;树的直径就是树中所有最短路经距离的最大值。 求树的直径通常有两种方法&#xff0c;一种是通过两次搜索&#xff08;bfs和dfs均可&#xff09;&#xff0c;另一种就是通过树形dp来求了。 先来介绍一下用两次深搜来求树的直径&#x…
阅读更多...
树的直径的概念

树的直径的概念

树的直径的定义: 在一棵树中&#xff0c;每一条边都有权值&#xff0c;树中的两个点之间的距离&#xff0c;定义为连接两点的路径上边权之和&#xff0c; 那么树上最远的两个点&#xff0c;他们之间的距离&#xff0c;就被称之为&#xff0c;树的直径。 树的直径的别称&#x…
阅读更多...
树的直径

树的直径

【定义】 我们将一棵树T ( V&#xff0c;E )的直径定义为maxδ ( u&#xff0c;v ) ( u&#xff0c;v ∈ V )&#xff0c;也就是说&#xff0c;树中所有最短路径距离的最大值即为树的直径。 【做法】 例题传送门Cow Marathon&#xff08;POJ 1985&#xff09; 对于树的直径…
阅读更多...
浅谈树的直径

浅谈树的直径

一、定义&#xff1a; 我们将一棵树T(V,E)的直径定义为max(u,v) (u,v∈V)&#xff0c;也就是说&#xff0c;树中所有最短路径距离的最大值即为树的直径。&#xff08;就是树中的最长路径的长度&#xff09; 二、求解树德直径&#xff1a; 求得树的直径有两种方法&#xff0c;一…
阅读更多...
推荐文章

Copyright @ 2022~2023