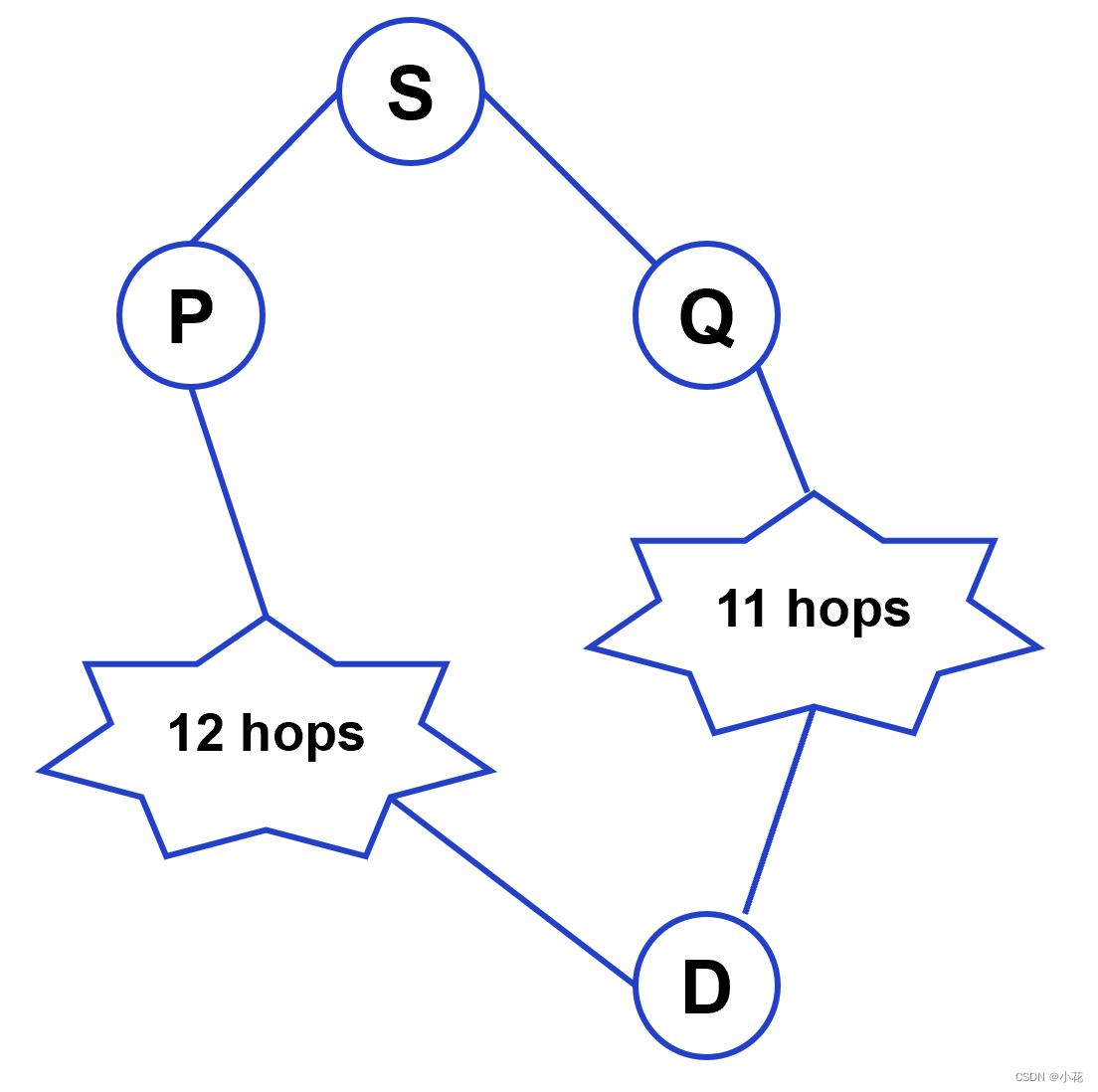
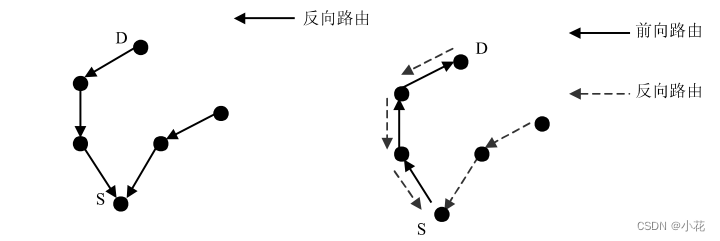
以下为两次dfs(bfs)的做法以及正确性证明。
算法步骤
(1)任取树上一点S,以S为源点BFS得S到各个顶点的d值;
(2)取d值最大者之一为P,再以P为源点BFS得P到各个顶点的d值;
(3)再取d值最大者之一为Q,PQ为树的其中一条直径。
算法的时间复杂度为两次BFS用时,即 2 O ( V + E ) 2O(V+E) 2O(V+E).
正确性证明:
假设AB为树的直径,且|AB|>|PQ|.
(1)若P为A或者B,则PQ=AB,|AB|=|PQ|,矛盾;
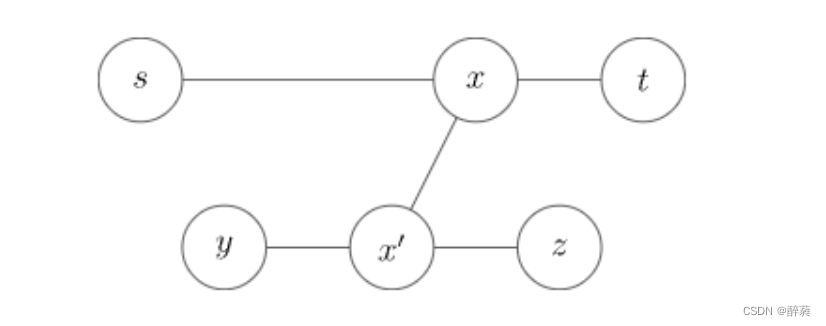
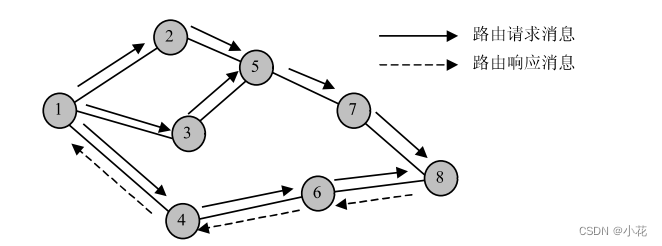
(2)若PQ与AB相交,设交点为C,如图
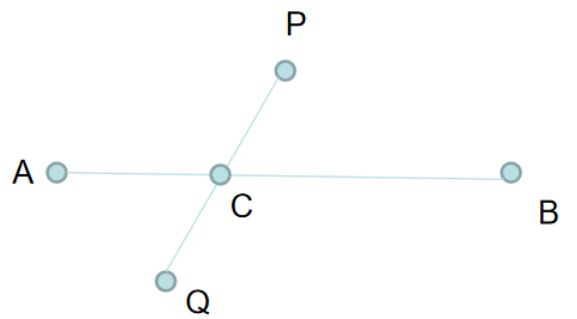
根据算法操作(2), ∣ P Q ∣ ≥ ∣ P A ∣ , ∣ P Q ∣ ≥ ∣ P B ∣ |PQ|\geq|PA|,|PQ|\geq|PB| ∣PQ∣≥∣PA∣,∣PQ∣≥∣PB∣,
减去公共部分得 ∣ C Q ∣ ≥ ∣ C A ∣ , ∣ C Q ∣ ≥ ∣ C B ∣ |CQ|\geq|CA|,|CQ|\geq|CB| ∣CQ∣≥∣CA∣,∣CQ∣≥∣CB∣,
对于 ∣ A Q ∣ = ∣ A C ∣ + ∣ C Q ∣ ≥ ∣ A C ∣ + ∣ C B ∣ = ∣ A B ∣ |AQ|=|AC|+|CQ|\geq|AC|+|CB|=|AB| ∣AQ∣=∣AC∣+∣CQ∣≥∣AC∣+∣CB∣=∣AB∣,同理 ∣ B Q ∣ ≥ ∣ A B ∣ |BQ|\geq|AB| ∣BQ∣≥∣AB∣,
由于AB为直径,且 ∣ A B ∣ > ∣ P Q ∣ |AB|>|PQ| ∣AB∣>∣PQ∣,只能有 ∣ C Q ∣ = ∣ C A ∣ = ∣ C B ∣ > ∣ C P ∣ |CQ|=|CA|=|CB|>|CP| ∣CQ∣=∣CA∣=∣CB∣>∣CP∣,
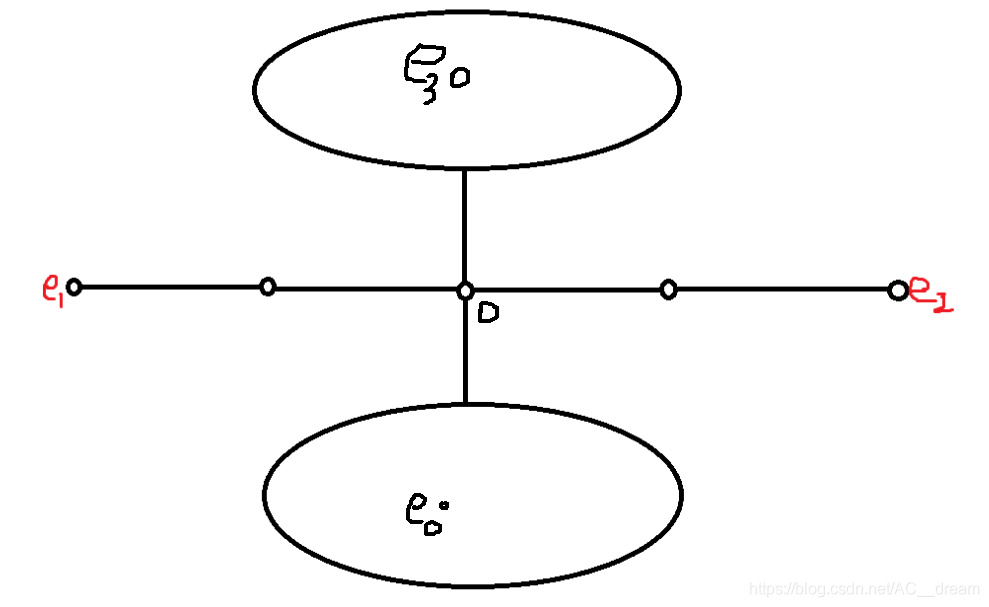
将树视为以C为根的树,设A,B,Q,P所在子树为{A},{B},{Q},{P},
S点在{A},{B},{Q},{P}其中之一,
根据算法操作(1), ∣ S P ∣ > ∣ S A ∣ |SP|>|SA| ∣SP∣>∣SA∣,S点只能在{A};
∣ S P ∣ > ∣ S B ∣ |SP|>|SB| ∣SP∣>∣SB∣,S点只能在{B};
∣ S P ∣ > ∣ S Q ∣ |SP|>|SQ| ∣SP∣>∣SQ∣,S点只能在{S};
综上,不存在这样的S点,矛盾;
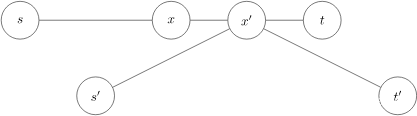
(3)若PQ与AB无交点,则设MN为两者联络线,如图
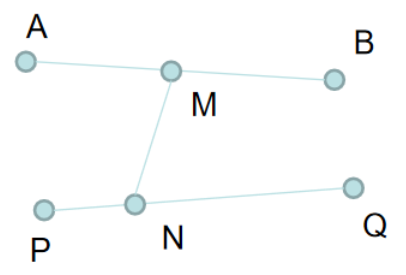
根据算法操作(2), ∣ P Q ∣ ≥ ∣ P A ∣ , ∣ P Q ∣ ≥ ∣ P B ∣ |PQ|\geq|PA|,|PQ|\geq|PB| ∣PQ∣≥∣PA∣,∣PQ∣≥∣PB∣,
减去公共部分得 ∣ N Q ∣ ≥ ∣ N A ∣ , ∣ N Q ∣ ≥ ∣ N B ∣ |NQ|\geq|NA|,|NQ|\geq|NB| ∣NQ∣≥∣NA∣,∣NQ∣≥∣NB∣,
容易得 ∣ Q M ∣ = ∣ N Q ∣ + ∣ M N ∣ > ∣ M A ∣ |QM|=|NQ|+|MN|>|MA| ∣QM∣=∣NQ∣+∣MN∣>∣MA∣,
因此, ∣ B Q ∣ = ∣ B M ∣ + ∣ Q M ∣ > ∣ B M ∣ + ∣ M A ∣ = ∣ A B ∣ |BQ|=|BM|+|QM|>|BM|+|MA|=|AB| ∣BQ∣=∣BM∣+∣QM∣>∣BM∣+∣MA∣=∣AB∣,与AB为树的直径相矛盾;
综上所述,假设不成立,PQ为树的直径.
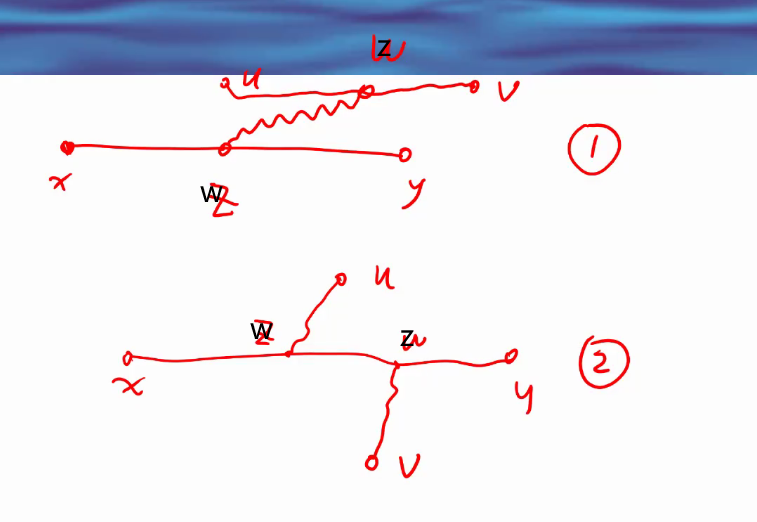
以下为老师ppt上的证明:


反证法,假设v不是直径的一个端点。 δ ( u , x ) ≥ δ ( u , w ) \delta(u,x)\geq\delta(u,w) δ(u,x)≥δ(u,w)的前提是不妨设路径 w → u w\rightarrow u w→u和 x → u x\rightarrow u x→u有公共点,取 w = v w=v w=v,而这与算法步骤中 δ ( u , v ) \delta(u,v) δ(u,v)最大相矛盾。

根据第一点图①不存在,这和我证明的第(3)点对应,但我否定了图①情况后并没有进一步推证 u v uv uv和 x y xy xy存在公共部分(不仅仅是我第(2)点提及只有一个交点)的情形。或者说我的证明分类讨论的对象是算法求解出的 P Q PQ PQ和假设直径 A B AB AB之间的关系,遗漏了该情形。从 ∀ u \forall u ∀u出发讨论更容易分类。