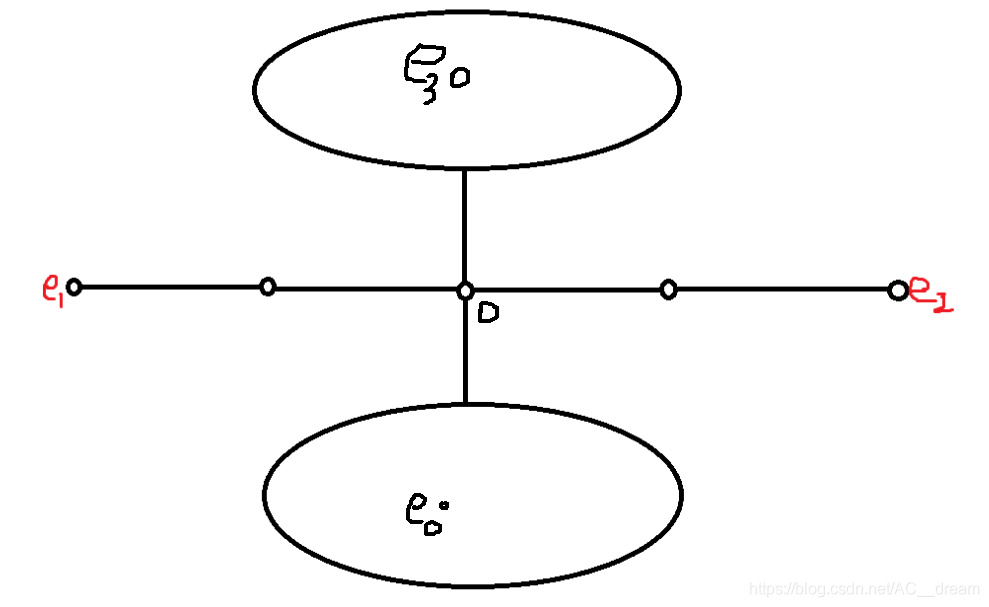
树的直径
一、定义
在一棵树中,最远的两个子节点之间的距离被称为树的直径;
链接这两个点的路径被称为树的最长链;
有两种求法,时间复杂度均为 O ( n ) O(n) O(n) ;
二、树形DP
1. 状态
由于一个点的最长路通过其子节点转移来,所以定义状态为
d p [ i ] dp[i] dp[i] 表示经过 i i i 点的最长路;
2. 转移
设有子树根结点为 i i i ,其子节点为 u 1 , u 2 , … , u n u_1, u_2, \dots , u_n u1,u2,…,un ;
则对于经过 i i i 结点的最长路,即为经过其子节点 u j u_j uj 与 u k u_k uk 的最长路和+经过 i i i 结点多走的两条边权;
则有
d p [ i ] = max { d p [ u j ] + d p [ u k ] + e d g e [ i ] [ j ] + e d g e [ j ] [ k ] } dp[i] = \max \{ dp[u_j] + dp[u_k] + edge[i][j] + edge[j][k] \} dp[i]=max{dp[uj]+dp[uk]+edge[i][j]+edge[j][k]}
但转移时,不需要将 j j j 与 k k k 具体值进行枚举,后连接 u j u_j uj 与 u k u_k uk ,只需要将 u j u_j uj 连接到 i i i 的子节点的最长路的最大值即可;
枚举 j j j 时, d p [ i ] dp[i] dp[i] 保存了从节点 i i i 出发走向以 u k ( k < j ) u_k \; (k < j) uk(k<j) 为根的子树能够到达的最远距离,这个距离为,
d p [ i ] = max 1 ≤ k < j { d p [ u k ] + e d g e [ i ] [ u k ] } dp[i] = \max_{1 \leq k < j} \{ dp[u_k] +edge[i][u_k] \} dp[i]=1≤k<jmax{dp[uk]+edge[i][uk]}
则此时经过 i i i 的最长路为 d p [ i ] + d p [ u j ] + e d g e [ i ] [ u j ] dp[i] + dp[u_j] + edge[i][u_j] dp[i]+dp[uj]+edge[i][uj] ,但不能将这个值来更新 d p [ i ] dp[i] dp[i] ,否则后面的转移不符合前提,则直接使用这个值更新答案,用 d p [ i ] = max { d p [ u j ] + e d g e [ i ] [ u j ] } dp[i] = \max\{dp[u_j] + edge[i][u_j] \} dp[i]=max{dp[uj]+edge[i][uj]} 更新 d p [ i ] dp[i] dp[i] ,即可;
3. 代码
以带边权的双向建边邻接表存储树为例;
void dfs(int i) {flag[i] = true;for (int t = 0; t < g[i].size(); t++) {int u = g[i][t].to, tot = g[i][t].tot;if (!flag[u]) {dfs(u);ans = max(ans, dp[i] + dp[u] + tot);dp[i] = max(dp[i], dp[u] + tot);}}return;
}
三、DFS
1. 思路
向下最长路 + 向下次长路 == 经过此点的最长路;
证明如下
有
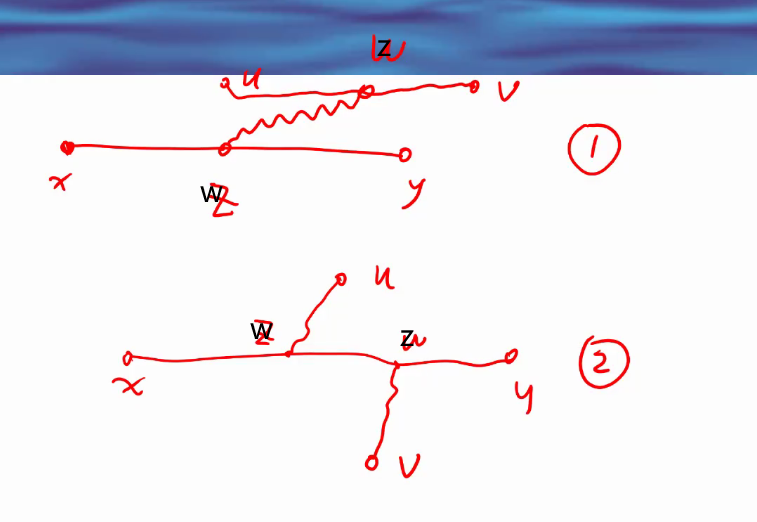
d o w n 1 [ i ] down1[i] down1[i] 表示 i i i 结点的向下最长路;
d o w n 2 [ i ] down2[i] down2[i] 表示 i 结点的向下次长路;
u p [ i ] up[i] up[i] 表示 i 结点的向上最长路;
有一节点 u u u ,其子节点为 i 1 i_1 i1 与 i 2 i_2 i2 ,父节点为 v v v ;

对于 u u u 点的最长路,有两种情况,
- u p [ u ] + d o w n 1 [ u ] up[u] + down1[u] up[u]+down1[u];
- d o w n 1 [ u ] + d o w n 2 [ u ] down1[u] + down2[u] down1[u]+down2[u];
则两种情况的最大值为经过 u u u 点的最长路;
若 u p [ u ] + d o w n 1 [ u ] up[u] + down1[u] up[u]+down1[u] 为最大值,则对于 u u u 的父节点 v v v ,过 v v v 的最短路为 d o w n 1 [ v ] + d o w n 2 [ v ] down1[v] + down2[v] down1[v]+down2[v] ,
即最长路为向下最长路 + 向下次长路;
则证明成立;
2. 实现
用一个 DFS 从上向下搜索,在返回时,用过子结点的最长路更新父节点的向下最长路;
关于向下次长路,有
当向下最长路值更新时,其原来的值便为向下次长路值;
则搜索每个结点的向下最长路与向下次长路;
直径便是向下最长与向下次长路的和的最大值;
3. 代码
以带边权的双向建边邻接表存储树为例;
void dfs1(int i) {flag[i] = true;for (int t = 0; t < g[i].size(); t++) {int v = g[i][t].to, tot = g[i][t].tot;if (!flag[v]) { dfs1(v);int val = down1[v] + tot;if (val > down1[i]) {down2[i] = down1[i];down1[i] = val;} else {down2[i] = max(down2[i], val);}}}ans = max(ans, down1[i] + down2[i]);return;
}
四、求直径的点
判断一点是否在直径上,即判断经过此点的最长路是否为直径即可;
因为有
向下最长路 + 向下次长路 = 经过此点的最长路;
所以存储向下最长路与向下次长路;
但是,又因为树的直径可能有多条,即树的直径经过一点时可能有两种情况,
-
将此点作为转折点,此时有
向下最长路 + 向下次长路 == 直径;
-
将此点作为不转折的点,此时有
向下最长路 + 向上最长路 == 直径;
所以还要存储向上最长路;
当一个点的 向下最长路 + 向下次长路 = 直径 或 向下最长路 + 向上最长路 = 直径 时,则说明此点在直径上;
求向上最长路
思路
从上向下搜索,用父节点的向上最长路更新子节点的向上最长路;
则有 i i i 为父结点, u u u 为子节点时, u u u 的向上最长路即为 i i i 的向上最长路与 i i i 的向下最长路的最大值;
u p [ u ] = max { max { u p [ i ] , d o w n 1 [ i ] } + e d g e [ i ] [ u ] } up[u] = \max \{ \max \{ up[i], down1[i] \} + edge[i][u] \} up[u]=max{max{up[i],down1[i]}+edge[i][u]}
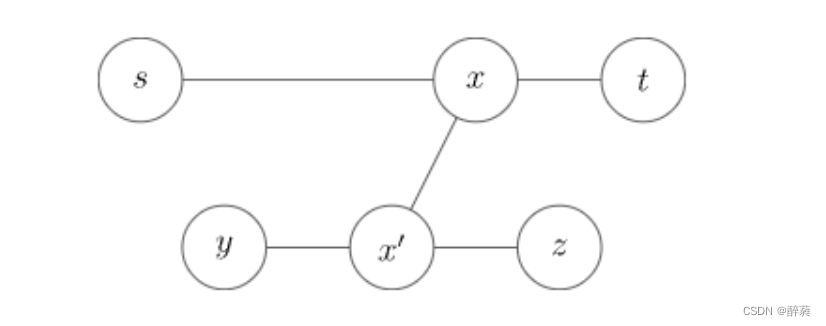
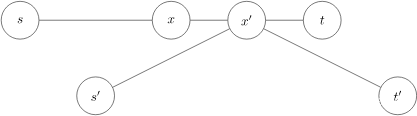
但是, i i i 的向下最长路可能包含 u u u ,即 d o w n 1 [ i ] − d o w n 1 [ u ] = = e d g e [ i ] [ u ] down1[i] - down1[u] == edge[i][u] down1[i]−down1[u]==edge[i][u] 时,此时则会重复走过 u u u 点;
所以此时判断是否有其余的 u 1 u_1 u1 使 d o w n 1 [ i ] − d o w n 1 [ u 1 ] = = e d g e [ i ] [ u 1 ] down1[i] - down1[u_1] == edge[i][u_1] down1[i]−down1[u1]==edge[i][u1] 成立;
若有,则说明上转移式可以满足,即从 u u u 走到父节点 i i i 经过满足条件的点 u 1 u_1 u1 向下走;
若没有,则说明上转移式最大值时不能取 d o w n 1 [ i ] down1[i] down1[i] 则取 d o w n 2 [ i ] down2[i] down2[i] ,即
u p [ u ] = max { max { u p [ i ] , d o w n 2 [ i ] } + e d g e [ i ] [ u ] } up[u] = \max \{ \max \{ up[i], down2[i] \} + edge[i][u] \} up[u]=max{max{up[i],down2[i]}+edge[i][u]}
代码
以带边权的双向建边邻接表存储树为例;
void dfs2(int i) {flag[i] = true;int ans = 0;for (int t = 0; t < g[i].size(); t++) {int v = g[i][t].to, tot = g[i][t].tot;if (!flag[v]) {if (down1[i] == down1[v] + tot) {ans++;}}}for (int t = 0; t < g[i].size(); t++) {int v = g[i][t].to, tot = g[i][t].tot;if (!flag[v]) {if (down1[i] != down1[v] + tot || (ans > 1 && down1[i] == down1[v] + tot)) {up[v] = max(up[v], max(up[i], down1[i]) + tot);} else {up[v] = max(up[v], max(up[i], down2[i]) + tot);}dfs2(v);}}return;
}
五、例题
旅游规划
题目描述
W 市的交通规划出现了重大问题,市政府下定决心在全市各大交通路口安排疏导员来疏导密集的车流。但由于人员不足,W 市市长决定只在最需要安排人员的路口安排人员。
具体来说,W 市的交通网络十分简单,由 n 个交叉路口和 n - 1 条街道构成,交叉路口路口编号依次为 0 , 1 , … , n − 1 0, 1, \dots , n - 1 0,1,…,n−1 。任意一条街道连接两个交叉路口,且任意两个交叉路口间都存在一条路径互相连接。
经过长期调查,结果显示,如果一个交叉路口位于 W 市交通网最长路径上,那么这个路口必定拥挤不堪。所谓最长路径,定义为某条路径 p = ( v 1 , v 2 , v 3 , ⋯ , v k ) p=(v_1,v_2,v_3,\cdots,v_k) p=(v1,v2,v3,⋯,vk) ,路径经过的路口各不相同,且城市中不存在长度大于 k 的路径,因此最长路径可能不唯一。因此 W 市市长想知道哪些路口位于城市交通网的最长路径上。
输入格式
第一行一个整数 n ;
之后 n - 1 行每行两个整数 u, v ,表示 u 和 v 的路口间存在着一条街道。
输出格式
输出包括若干行,每行包括一个整数——某个位于最长路径上的路口编号。为了确保解唯一,请将所有最长路径上的路口编号按编号顺序由小到大依次输出。
分析
此题意为求直径上的点;
代码
#include <cstdio>
#include <vector>
#include <algorithm>
#define MAXN 200005
using namespace std;
int n, down1[MAXN], down2[MAXN], up[MAXN], dis = -1;
bool flag[MAXN];
vector < int > g[MAXN];
void dfs1(int i) {flag[i] = true;for (int t = 0; t < g[i].size(); t++) {int v = g[i][t];if (!flag[v]) { dfs1(v);int tot = down1[v] + 1;if (tot > down1[i]) {down2[i] = down1[i];down1[i] = tot;} else {down2[i] = max(down2[i], tot);}}}flag[i] = false;dis = max(dis, down1[i] + down2[i]);return;
}void dfs2(int i) {flag[i] = true;int tot = 0;for (int t = 0; t < g[i].size(); t++) {int v = g[i][t];if (!flag[v]) {if (down1[i] == down1[v] + 1) {tot++;}}}for (int t = 0; t < g[i].size(); t++) {int v = g[i][t];if (!flag[v]) {if (down1[i] != down1[v] + 1 || (tot > 1 && down1[i] == down1[v] + 1)) {up[v] = max(up[v], max(up[i], down1[i]) + 1);} else {up[v] = max(up[v], max(up[i], down2[i]) + 1);}dfs2(v);}}return;
}
int main() {scanf("%d", &n);for (int i = 1; i < n; i++) {int x, y;scanf("%d %d", &x, &y);g[x].push_back(y);g[y].push_back(x);}dfs1(0);dfs2(0);for (int i = 0; i < n; i++) {if (down1[i] + max(down2[i], up[i]) == dis) {printf("%d\n", i);}}return 0;
}