题目地址:https://leetcode-cn.com/problems/tree-diameter/
1245. 树的直径
难度中等48收藏分享切换为英文接收动态反馈
给你这棵「无向树」,请你测算并返回它的「直径」:这棵树上最长简单路径的 边数。
我们用一个由所有「边」组成的数组 edges 来表示一棵无向树,其中 edges[i] = [u, v] 表示节点 u 和 v 之间的双向边。
树上的节点都已经用 {0, 1, ..., edges.length} 中的数做了标记,每个节点上的标记都是独一无二的。
示例 1:
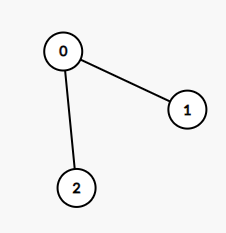
输入:edges = [[0,1],[0,2]]
输出:2
解释:
这棵树上最长的路径是 1 - 0 - 2,边数为 2。
示例 2:
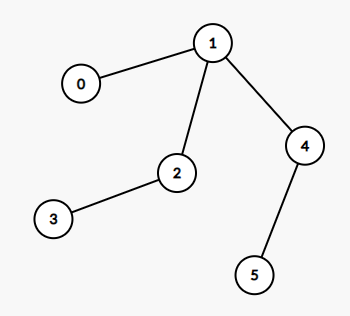
输入:edges = [[0,1],[1,2],[2,3],[1,4],[4,5]]
输出:4
解释:
这棵树上最长的路径是 3 - 2 - 1 - 4 - 5,边数为 4。
提示:
0 <= edges.length < 10^4edges[i][0] != edges[i][1]0 <= edges[i][j] <= edges.lengthedges会形成一棵无向树
两次BFS遍历
第一次遍历求出离当前节点最远的点
第二次遍历求出离 第一次最远的 点
两点之间的距离就是树的直径
时间复杂度O(N)
空间复杂度O(N)
Map<Integer, Set<Integer>> graph = new HashMap();public int treeDiameter(int[][] edges){for(int i = 0; i < edges.length; i++){add(edges[i][0], edges[i][1]); add(edges[i][1], edges[i][0]);}int[] ints = bfs(0);int[] bfs = bfs(ints[0]);return bfs[1];}public int[] bfs(int cur){Set<Integer> st = new HashSet();st.add(cur);Queue<int[]> q = new LinkedList();q.offer(new int[]{cur, 0});int farthestNode = -1, farthestDist = 0;while (!q.isEmpty()){int[] poll = q.poll();farthestNode = poll[0];farthestDist = poll[1];for(Integer ne: graph.get(farthestNode)){if(!st.contains(ne)){st.add(ne);q.offer(new int[]{ne, farthestDist + 1});}}}return new int[]{farthestNode, farthestDist};}public void add(int a, int b){graph.putIfAbsent(a, new HashSet());graph.get(a).add(b);}
1617. 统计子树中城市之间最大距离
https://leetcode-cn.com/problems/count-subtrees-with-max-distance-between-cities/
给你 n 个城市,编号为从 1 到 n 。同时给你一个大小为 n-1 的数组 edges ,其中 edges[i] = [ui, vi] 表示城市 ui 和 vi 之间有一条双向边。题目保证任意城市之间只有唯一的一条路径。换句话说,所有城市形成了一棵 树 。
一棵 子树 是城市的一个子集,且子集中任意城市之间可以通过子集中的其他城市和边到达。两个子树被认为不一样的条件是至少有一个城市在其中一棵子树中存在,但在另一棵子树中不存在。
对于 d 从 1 到 n-1 ,请你找到城市间 最大距离 恰好为 d 的所有子树数目。
请你返回一个大小为 n-1 的数组,其中第 d 个元素(下标从 1 开始)是城市间 最大距离 恰好等于 d 的子树数目。
请注意,两个城市间距离定义为它们之间需要经过的边的数目。
示例 1:
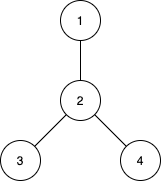
输入:n = 4, edges = [[1,2],[2,3],[2,4]]
输出:[3,4,0]
解释:
子树 {1,2}, {2,3} 和 {2,4} 最大距离都是 1 。
子树 {1,2,3}, {1,2,4}, {2,3,4} 和 {1,2,3,4} 最大距离都为 2 。
不存在城市间最大距离为 3 的子树。
示例 2:
输入:n = 2, edges = [[1,2]]
输出:[1]
示例 3:
输入:n = 3, edges = [[1,2],[2,3]]
输出:[2,1]
提示:
2 <= n <= 15
edges.length == n-1
edges[i].length == 2
1 <= ui, vi <= n
题目保证 (ui, vi) 所表示的边互不相同。