使用python模拟实现PID控制算法

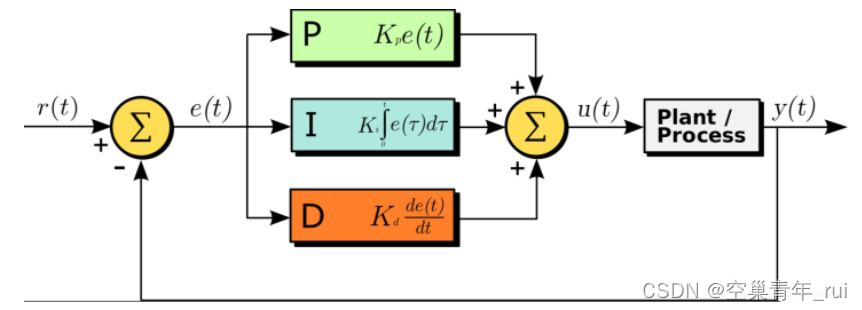
PID控制算法是工业应用中最广泛算法之一，在闭环系统的控制中，可自动对控制系统进行准确且迅速的校正。
P、I、D分别是“比例（proportional）、积分（integral）、微分（derivative）”三个单词的首字母，他们分别对应算法中使用的三个参数。
有关于PID算法的详细内容请自行查阅相关资料，参考文章。

常用的PID控制算法有位置式和增量式两种形式，下面给出他们的python实现：

1. 位置式

位置式PID离散公式：$u(k)=K_p{e}_k+K_i{\sum }_{i=1}^{k}e(i)\Delta t+K_d\frac{e(k)-e(k-1)}{\Delta t}$
位置式可以简单理解为算法每次计算得出值的都是要走到的点。如我们的目标是让一辆车前进10米，算法第一次计算得出的值是7.3，则表示车第一次运动来到了7.3米的位置。

class PositionPID(object):"""位置式PID算法实现"""def __init__(self, target, cur_val, dt, max, min, p, i, d) -> None:self.dt = dt  # 循环时间间隔self._max = max  # 最大输出限制，规避过冲self._min = min  # 最小输出限制self.k_p = p  # 比例系数self.k_i = i  # 积分系数self.k_d = d  # 微分系数self.target = target  # 目标值self.cur_val = cur_val  # 算法当前PID位置值，第一次为设定的初始位置self._pre_error = 0  # t-1 时刻误差值self._integral = 0  # 误差积分值def calculate(self):"""计算t时刻PID输出值cur_val"""error = self.target - self.cur_val  # 计算当前误差# 比例项p_out = self.k_p * error  # 积分项self._integral += (error * self.dt)i_out = self.k_i * self._integral# 微分项derivative = (error - self._pre_error) / self.dtd_out = self.k_d * derivative# t 时刻pid输出output = p_out + i_out + d_out# 限制输出值if output > self._max:output = self._maxelif output < self._min:output = self._minself._pre_error = errorself.cur_val = outputreturn self.cur_valdef fit_and_plot(self, count = 200):"""使用PID拟合setPoint"""counts = np.arange(count)outputs = []for i in counts:outputs.append(self.calculate())print('Count %3d: output: %f' % (i, outputs[-1]))print('Done')# print(outputs)plt.figure()plt.axhline(self.target, c='red')plt.plot(counts, np.array(outputs), 'b.')plt.ylim(min(outputs) - 0.1 * min(outputs), max(outputs) + 0.1 * max(outputs))plt.plot(outputs)plt.show()

运行测试：

pid = PositionPID(10, -5, 0.5, 100, -100, 0.2, 0.1, 0.01)
pid.fit_and_plot(150)

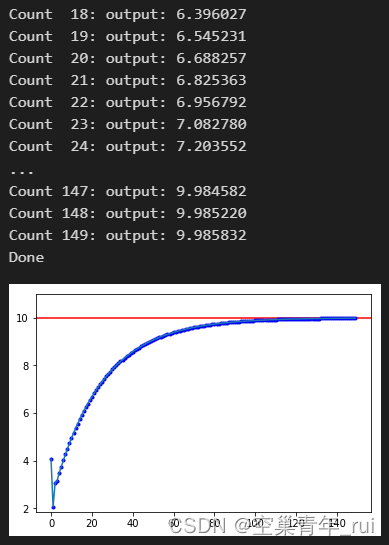
2. 增量式

增量式PID离散公式：$\Delta u(k)=K_p(e(k)-e(k-1))+K_{i}e(k)+K_d(e(k)-2e(k-1)+e(k-2))$
增量式可以简单理解为算法每次的计算值都是本次移动的步长。如我们的目标是让一辆车前进10米，车辆的当前位置在3米处，算法本次计算得出的值是2.5，则表示车本次需要前进2.5米，来到了5.5米的位置。

class DeltaPID(object):"""增量式PID算法实现"""def __init__(self, target, cur_val, dt, p, i, d) -> None:self.dt = dt  # 循环时间间隔self.k_p = p  # 比例系数self.k_i = i  # 积分系数self.k_d = d  # 微分系数self.target = target  # 目标值self.cur_val = cur_val  # 算法当前PID位置值self._pre_error = 0  # t-1 时刻误差值self._pre_pre_error = 0  # t-2 时刻误差值def calcalate(self):error = self.target - self.cur_valp_change = self.k_p * (error - self._pre_error)i_change = self.k_i * errord_change = self.k_d * (error - 2 * self._pre_error + self._pre_pre_error)delta_output = p_change + i_change + d_change  # 本次增量self.cur_val += delta_output  # 计算当前位置self._pre_pre_error = self._pre_errorself._pre_error = errorreturn self.cur_valdef fit_and_plot(self, count=200):counts = np.arange(count)outputs=[]for i in counts:outputs.append(self.calcalate())print('Count %3d: output: %f' % (i, outputs[-1]))print('Done')plt.figure()plt.axhline(self.target, c='red')plt.plot(counts, np.array(outputs), 'b.')plt.ylim(min(outputs) - 0.1 * min(outputs),max(outputs) + 0.1 * max(outputs))plt.plot(outputs)plt.show()

运行测试：

pid = DeltaPID(100, -80, 0.5, 0.2, 0.1, 0.001)
pid.fit_and_plot(150)

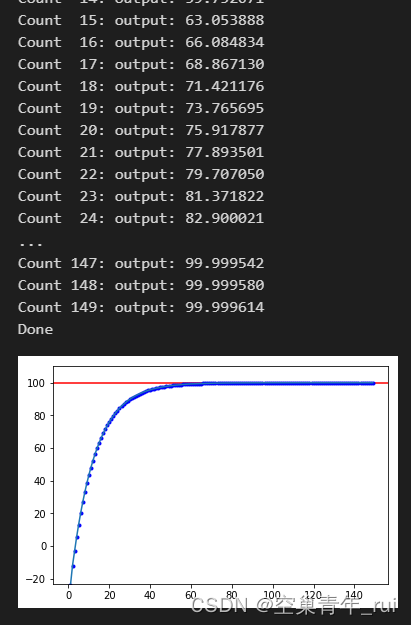
注意

算法中P、I、D三个超参数的初始值对算法的影响很大，不合适的设置可能会导致算法不收敛。调参方法可以搜索相关资料。

如，在位置式算法中，我们使用和上面例子同样的目标值和初始值，改变参数值：

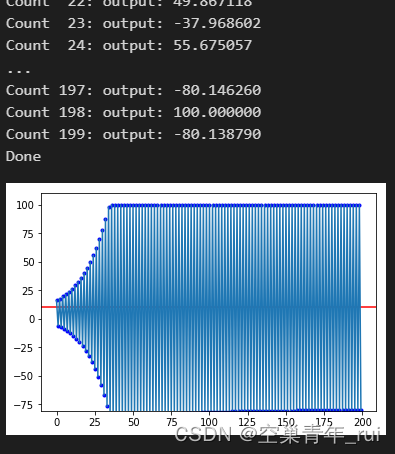
# 不合适的参数值
pid = PositionPID(10, -5, 0.5, 100, -100, 1, 0.1, 0.01)
pid.fit_and_plot()