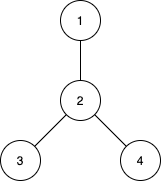
1.树包括有根树和无根树,有根树是有向图的子图,无根树是无向图的子图,都满足边数等于节点数减一。根是入度为零或没有父亲的节点
2.树的直径:树上最长的简单路径(不重复经过点的路径)
3.求解算法(主要是指无根树):在树上任选一点u,通过搜索求得距离它最远的节点v,再从点v出发,通过搜索得到距离它最远的点x,v到x的路径即为这棵树的直径
具体如下:
(1),第一次dfs
(2),第二次dfs
(3)dis(v,x)为直径
4.例:P3304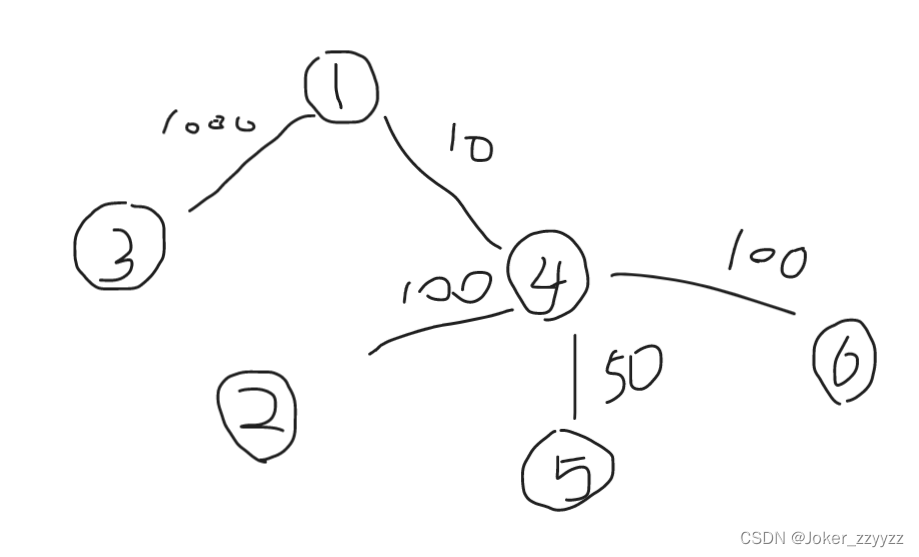
#include <bits/stdc++.h>
#define N 200005using namespace std;int n;
int farthestpoint;//第一次dfs得到的最远点是第二次dfs的起点
int maxlen;//树的直径struct edge
{int v , w;//v表示终点,w表示权值
};vector<edge> G[N];void dfs(int u , int father , int len)//father是u的父亲
{if(len > maxlen){maxlen = len;farthestpoint = u;for(int i = 0; i < G[u].size(); i++){int v = G[u][i].v;if(v != father)//不走回头路,不需要标记,没有环{dfs(v , u , len + G[u][i].w);}}}
}int main()
{cin >> n;for(int i = 1; i < n; i++){int a , b , c;cin >> a >> b >> c;G[a].push_back({b , c});G[b].push_back({a , c});}maxlen = -1;dfs(1 , 0 , 0);maxlen = -1;dfs(farthestpoint , 0 , 0);cout << farthestpoint << ' ' << maxlen;return 0;
}
1.树的重心:指树上的某个节点,如果以该节点为根,该节点所有子树数量的最大值最小
2.性质:
(1)重心到其它点的距离之和最小,重心不唯一,如果有两个重心,它们的距离和一样
(2)如果以某个节点为整棵树(节点数为n)的根,那么它的每棵子树的大小都<=n/2
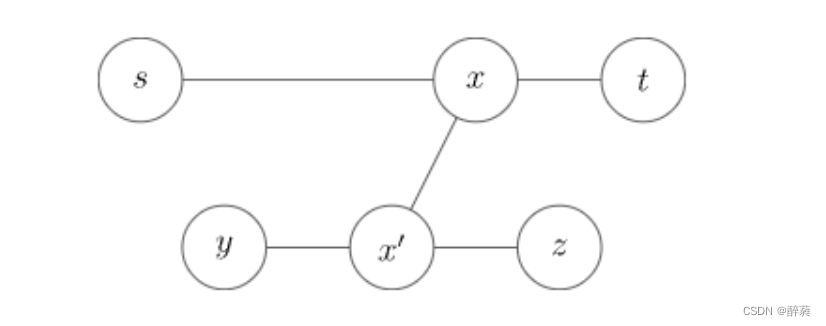
(3)一棵树如果添加或者删除一个节点,树的重心至多只移动一条边的位置
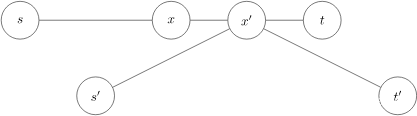
(4)把两棵树通过某个点相连得到一棵新树,新树的重心必然在两棵树重心的路径上
3.算法实现(dfs):
(1)任选一个节点为根,把无根树变成有根树。设f[i]表示以i为根的子树节点个数,由此可得,f[i]=sum(f[j])+1,j是i的子树
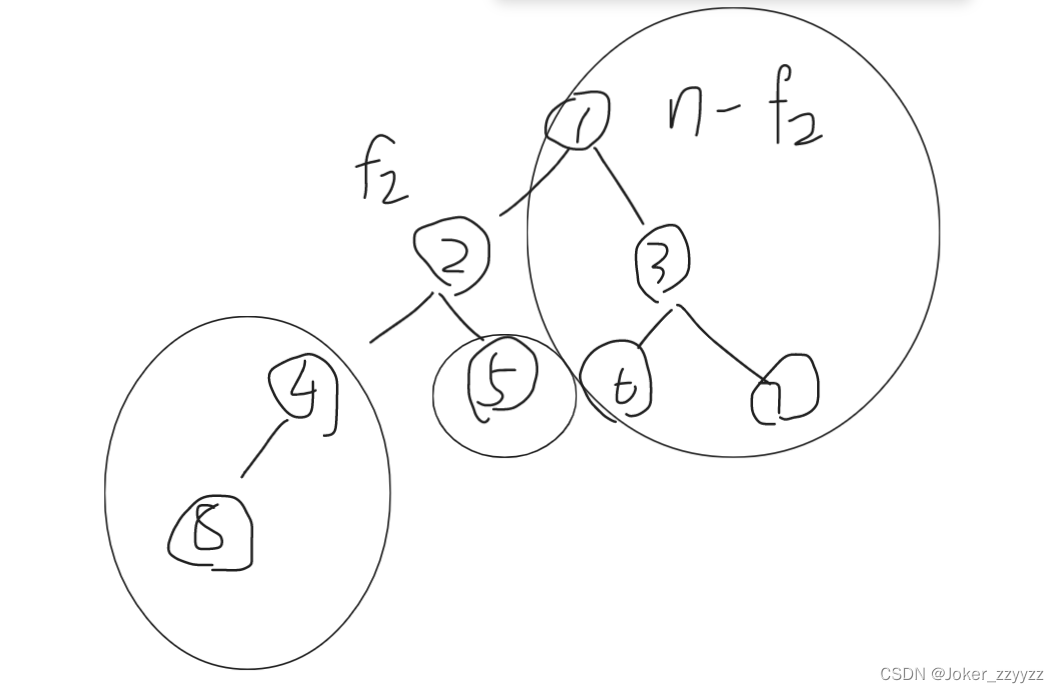
(2)所求节点i的最大子树的节点数为max[i]=max(f[j],n-f[i]),j是i的孩子