题目
实验室里原先有一台电脑(编号为1),最近氪金带师咕咕东又为实验室购置了N-1台电脑,编号为2到N。每台电脑都用网线连接到一台先前安装的电脑上。但是咕咕东担心网速太慢,他希望知道第i台电脑到其他电脑的最大网线长度,但是可怜的咕咕东在不久前刚刚遭受了宇宙射线的降智打击,请你帮帮他。

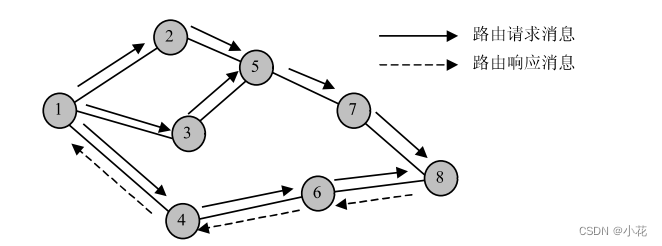
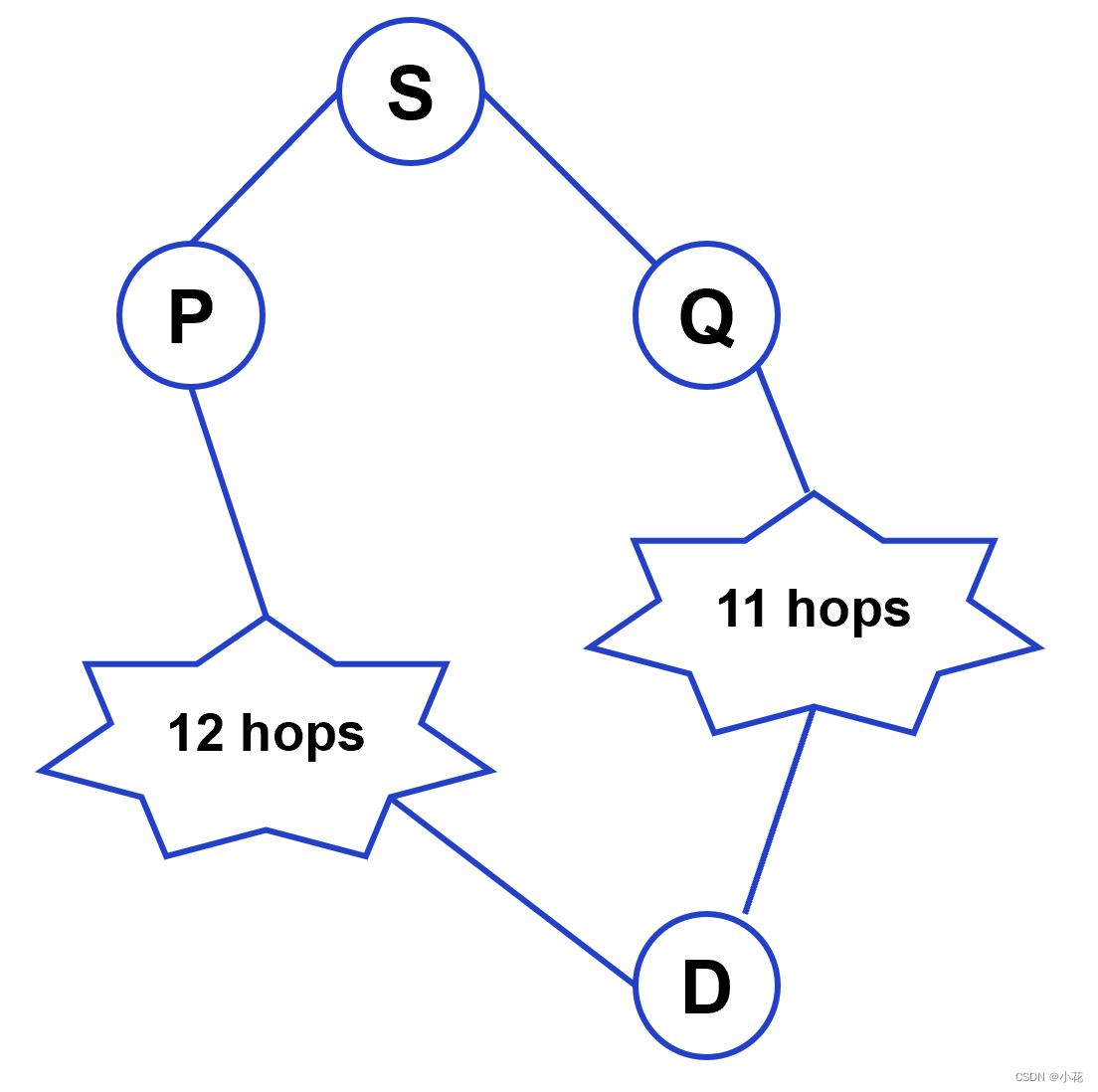
提示: 样例输入对应这个图,从这个图中你可以看出,距离1号电脑最远的电脑是4号电脑,他们之间的距离是3。 4号电脑与5号电脑都是距离2号电脑最远的点,故其答案是2。5号电脑距离3号电脑最远,故对于3号电脑来说它的答案是3。同样的我们可以计算出4号电脑和5号电脑的答案是4.
Input
输入文件包含多组测试数据。对于每组测试数据,第一行一个整数N (N<=10000),接下来有N-1行,每一行两个数,对于第i行的两个数,它们表示与i号电脑连接的电脑编号以及它们之间网线的长度。网线的总长度不会超过10^9,每个数之间用一个空格隔开。
output
对于每组测试数据输出N行,第i行表示i号电脑的答案 (1<=i<=N).
Sample inuput
5
1 1
2 1
3 1
1 1
Sample output
3
2
3
4
4
解题思路
1.最简单的想法是,对于每个点,都用一次dfs遍历,然后找到该点的最远距离的点,但是太慢了。
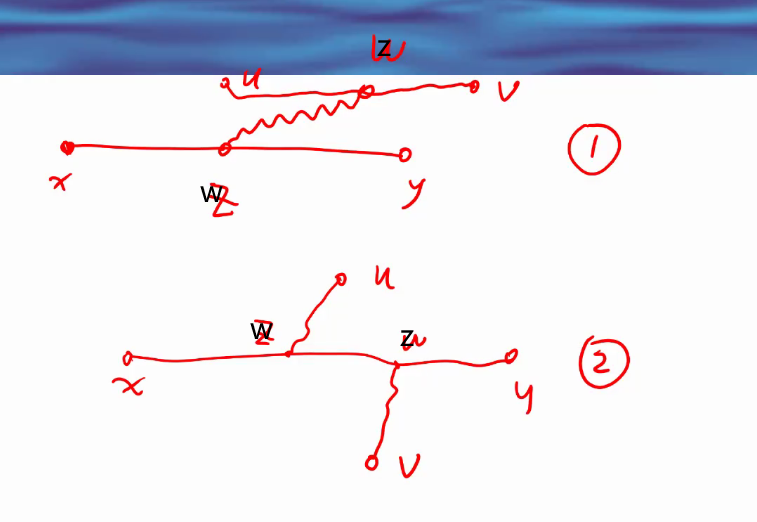
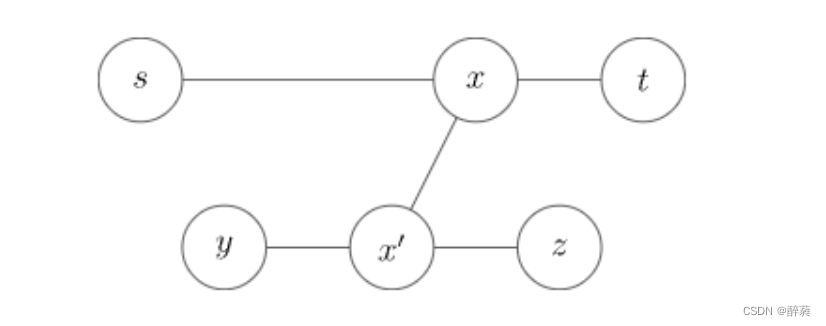
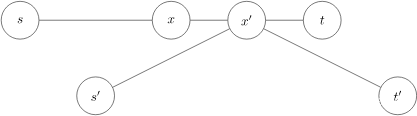
2.我们采用求树直径的方法,大概意思是,任意一个起点,我们对他进行dfs,然后找到离它最远的那个叶子节点1,然后从叶节点1再进行遍历,找到离他最远的叶子节点2。那么,叶1和叶2之间的距离就是树的直径,即这棵树内两点距离最远的距离。
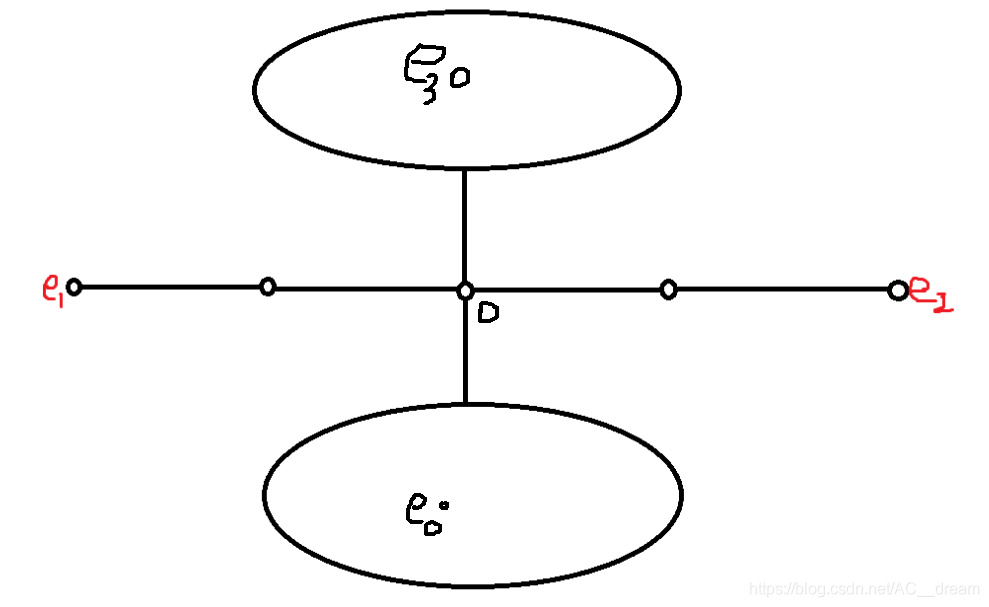
3.利用上面的算法,我们可以知道,一个节点到最远的节点3,节点3不是叶1就是叶2 。所以我们只要求出叶1和叶2,就可以求出每个点距离最远的点距离是多少。
代码实现
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int Max = 11000;
int max1,max2; //分别记录两个最远叶
int vis[Max]; //dfs的vis数组
int vi; //对应vis数组的值
long long M1[Max],M2[Max]; //每个点到左边最远叶和右边最远叶的距离//比较他们,就可以得到最大距离
long long MAX;
long long sum;
int N;void ini(); //局部初始化
void initial(); //完全初始化
void dfs( int x ,int X);
void addE(int u,int v,int w); //添加边操作struct edge{ //边集int u,v,w;
};
vector<edge> G[Max]; //邻接表struct OFMP{int point;long long sum;
};
OFMP oneOFmaxPoint; //记录一个最大叶和他的到起始点的距离int main()
{ios::sync_with_stdio(0);int v_,w_;while(cin>>N){for(int i=2;i<=N;i++){cin>>v_>>w_;addE(i,v_,w_);ini();dfs(1,0); //从第一台电脑开始找第一个最大叶max1 = oneOFmaxPoint.point; ini();dfs(max1,2); //从第一个最大叶找第二个最大叶max2 = oneOFmaxPoint.point;//这两个dfs都记录了第i个点到第一或第二个最大叶的距离ini();dfs(max2,3); //从第二个最大叶遍历到第一个最大叶for(int i=1;i<=N;i++){MAX = max(M1[i],M2[i]); //比较2个最大方向的距离cout<<MAX<<endl; }initial();}return 0;
}}void addE(int u,int v,int w)
{edge E1;E1.u=u,E1.v=v,E1.w=w;G[u].push_back(E1);edge E2;E2.u = v ,E2.v = u,E2.w = w;G[v].push_back(E2);
}void dfs( int x ,int X)
{vis[x] = vi;for(int i=0;i<G[x].size();i++) {//cout<<"1 ";if( vis[ G[x][i].v ] != vi) //不是叶break;// cout<<"2 ";if( i == G[x].size() -1 ) //是叶节点 {//维护路径大小和叶 // cout<<"3 ";if( sum > oneOFmaxPoint.sum )oneOFmaxPoint.sum = sum , oneOFmaxPoint.point= x;return ;} }for(int i=0;i<G[x].size();i++){if(vis[ G[x][i].v ] != vi){vis[ G[x][i].v ] = vi;sum += (long long)G[x][i].w;if(X==2) M1[ G[x][i].v ] = sum;//更新第一个最大叶子节点遍历结果if(X==3) M2[ G[x][i].v ] = sum;//更新第二个最大叶子节点遍历结果dfs( G[x][i].v , X);sum -= (long long)G[x][i].w;}}
}void ini()
{vi++;oneOFmaxPoint.point=0 ,oneOFmaxPoint.sum=0;sum = 0;
}void initial()
{oneOFmaxPoint.point=0 ,oneOFmaxPoint.sum=0;MAX = 0;for( int i=0;i<=N;i++ ) {M1[i]=0;M2[i]=0;G[i].clear();}
}
小结
每次得到结果后,一定要初始化,已经掉进这个坑里很多次了。