首先先介绍一下什么是树的直径，树的直径就是树中所有最短路经距离的最大值。

求树的直径通常有两种方法，一种是通过两次搜索（bfs和dfs均可），另一种就是通过树形dp来求了。

先来介绍一下用两次深搜来求树的直径：

先从图上任意一点，搜索整棵树，找到距离该点最远的点，再用距离该点最远的点搜索一次，即可得到树的直径。

现在来给出证明：

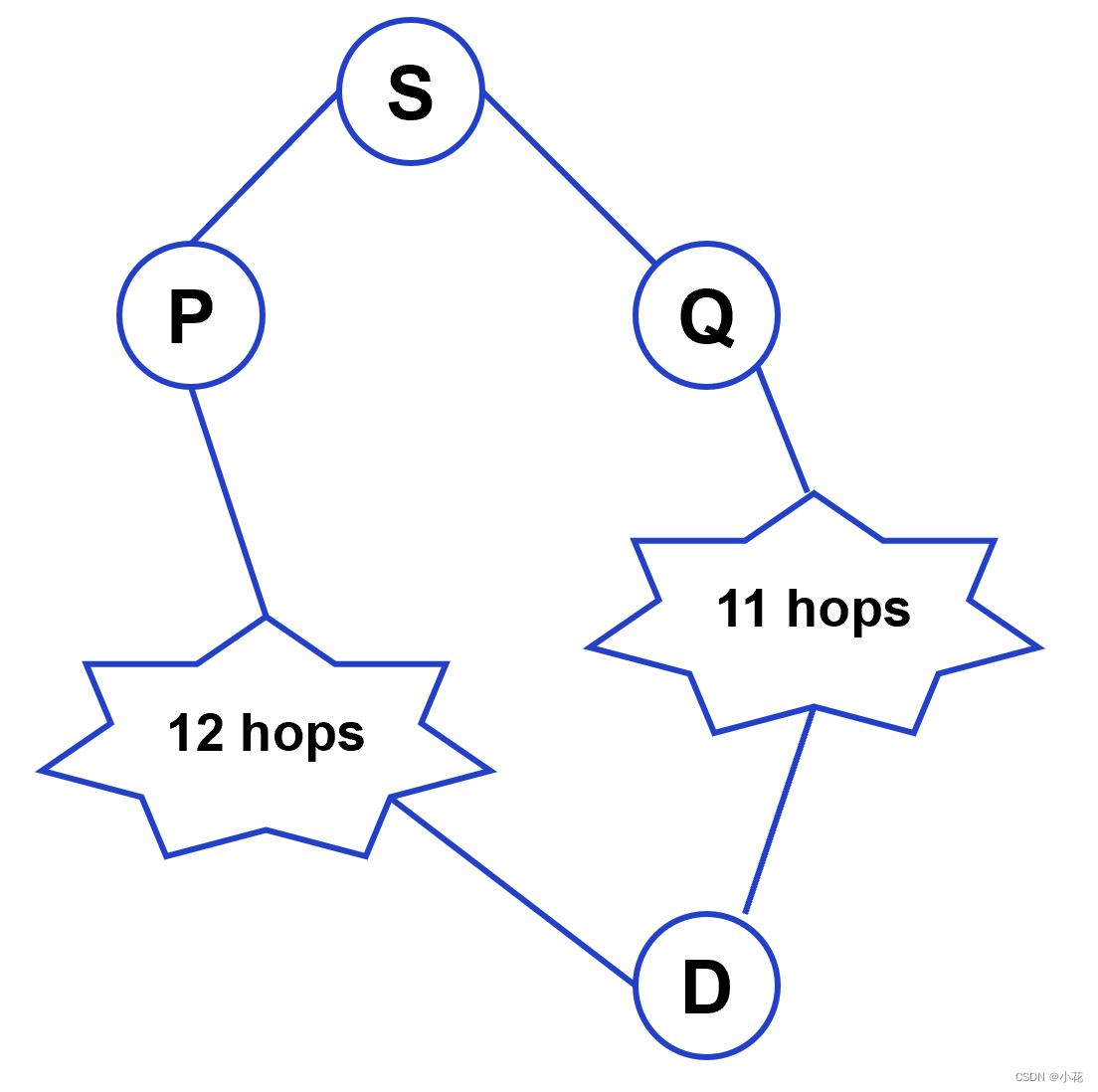
图像说明，两个椭圆形代表抽象子树，使得结论具有一般性：

由直径的定义我们可以知道由直径的一个端点搜索出的最大距离一定是直径的长度，那么我们现在就要证明由图中随机的一个点搜索出来的最远点一定是直径的一个端点，下面主要用反证法来证明。

以下图形均假设e1 e2为直径两端点

第一种情况，我们一开始所选取的点在直径上

我们一开始选定的点是e0，假如通过e0搜到的距离最远的点是e3，则说明

d（e0，o）+d（o，e3）>= d（e0，o）+d（o，e2），等价于

d（o，e3）>= d（o，e2）则 d（e1，o）+d（o，e3）>= d（e1，o）+d（o，e2）这与e1，e2是直径的两个端点矛盾，故不成立

第二种情况：我们一开始所选取的点不在直径上，且e0与e3与直径不相交，设直径上的o点与e0，e3路径上的e4点相交

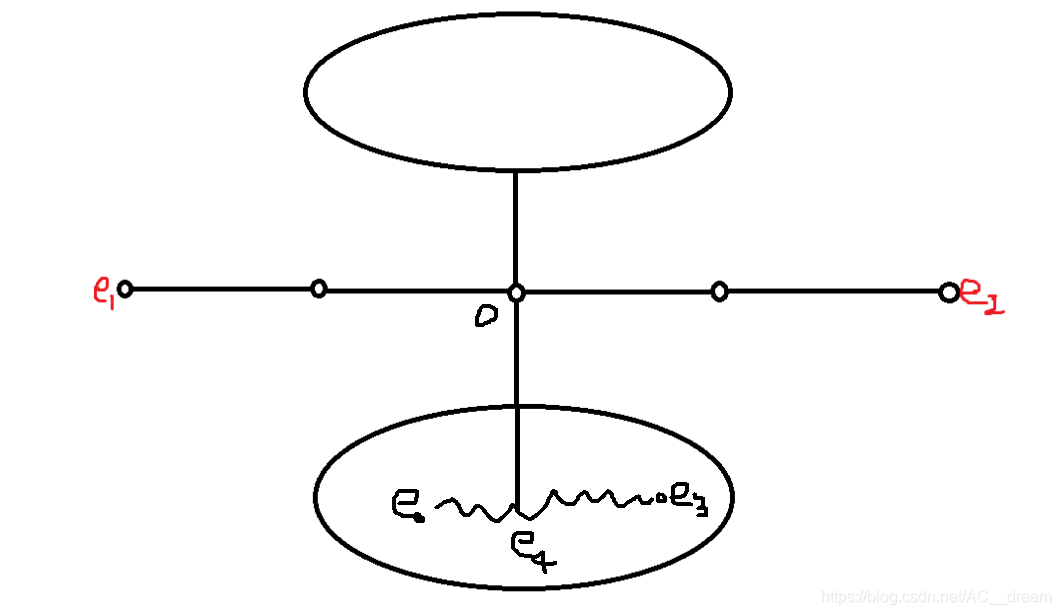
则d（e0，e4）+ d（e4，e3）>= d（e0，e4）+ d（e4，o）+d（o，e2）

等价于 d（e4，e3）>= d（e4，o）+d（o，e2）

则d（e1，o）+  d（o，e4）+ d（e4，e3）>=d（e1，o）+ d（o，e2）

这与e1，e2是直径的两个端点矛盾，故不成立

最后一种情况：我们一开始所选取的点不在直径上，且e0与e3与直径相交，不妨设交点为o

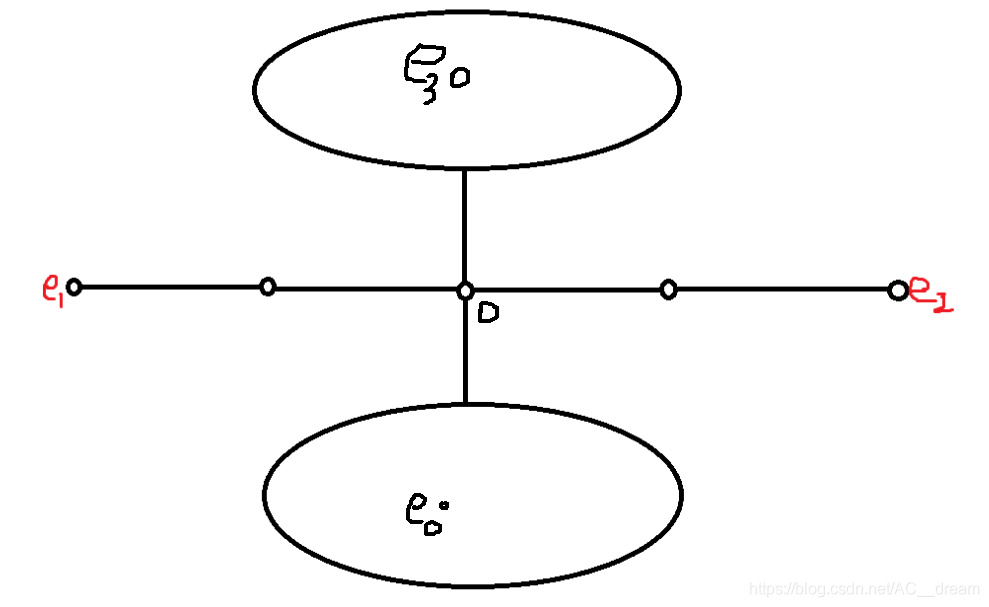
则d（e0，o）+d（o，e3）>= d（e0，o）+d（o，e2），等价于

d（o，e3）>= d（o，e2）则 d（e1，o）+d（o，e3）>= d（e1，o）+d（o，e2）

 这与e1，e2是直径的两个端点矛盾，故不成立

希望大家好好理解这个图，在以后的很多关于树的直径的题目中的结论证明方法都类似于上面的证明方法。

核心代码：

void dfs(int x,int father)
{for(int i=h[x];i!=-1;i=ne[i])//用链式前向星存树{int j=e[i];if(j==father) continue;//树是一种有向无环图，只要搜索过程中不返回父亲节点即可保证不会重复遍历同一个点。d[j]=d[x]+w[i];//更新每个点到起始点的距离（在树中任意两点的距离是唯一的）dfs(j,x);//继续搜索下一个节点}
}

ll ans=-1;for(int i=1;i<=n;i++)if(d[i]>ans){ans=d[i];e=i;记录与搜索点距离最远的点}

下面我来介绍一下树形dp来求树的直径：

不难想到，距离直径上的一个点最远的点和次远的点一定是直径的两个顶点，所以我们只要能找到距离每一个点的最远距离和次远距离不就能找到树的直径了么，但是有一点需要注意，就是距离一个点的最远距离和次远距离不能与重合部分。下面我来对具体实现方面展开说明。

我们需要开两个数组F1[]和F2[]分别记录到某个点的最远距离和次远距离，这样我们最后把每个点的两个数组相加取个最大值就可以找到树的直径了。

核心代码：

void dp(int x,int father)
{for(int i=h[x];i!=-1;i=ne[i])链式前向星存树{int j=e[i];if(j==father) continue;//防止原路返回dp(j,x);//dp过程应该是由叶节点开始的，也就是说先递归到叶节点再开始进行状态转移if(f1[x]<f1[j]+w[i])//如果子节点的最大距离+子节点与父节点之间边的权重大于父节点的最大距离，那么父节点的最大距离和次大距离都要得到相应更新{f2[x]=f1[x];f1[x]=f1[j]+w[i];}else if(f2[x]<f1[j]+w[i])//若子节点的最大距离+子节点与父节点之间边的权重小于父节点的最大距离，再判断与父节点的次大距离的关系f2[x]=f1[j]+w[i];ans=max(ans,f1[x]+f2[x]);//在搜索过程中找到树的直径}
}

下面我将给出一道例题，并用两种方法给出解答：

After hearing about the epidemic of obesity in the USA, Farmer John wants his cows to get more exercise, so he has committed to create a bovine marathon for his cows to run. The marathon route will include a pair of farms and a path comprised of a sequence of roads between them. Since FJ wants the cows to get as much exercise as possible he wants to find the two farms on his map that are the farthest apart from each other (distance being measured in terms of total length of road on the path between the two farms). Help him determine the distances between this farthest pair of farms.

Input

* Lines 1.....: Same input format as "Navigation Nightmare".

Output

* Line 1: An integer giving the distance between the farthest pair of farms.

Sample Input

7 6
1 6 13 E
6 3 9 E
3 5 7 S
4 1 3 N
2 4 20 W
4 7 2 S

Sample Output

52

我大概简化下题意吧：就是先输入两个整数，第一个整数表示点的数量，第二个整数表示边的数量，下面给出每条边的起始点和终止点以及该边的权值和方向（具体方向是用不到的，计算机中的方向只需考虑始点与终点即可），求该树的直径。

代码1（dfs）

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
using namespace std;
const int N=1000013;
typedef long long ll;
ll h[N],ne[N],e[N],idx,d[N],w[N];
bool vis[N];
void add(int x,int y,int z)
{e[idx]=y;w[idx]=z;ne[idx]=h[x];h[x]=idx++;
}
void dfs(int x,int father)
{for(int i=h[x];i!=-1;i=ne[i])//用链式向前星存树{int j=e[i];if(j==father) continue;//树是一种有向无环图，只要搜索过程中不返回父亲节点即可保证不会重复遍历同一个点。d[j]=d[x]+w[i];//更新每个点到起始点的距离（在树中任意两点的距离是唯一的）dfs(j,x);//继续搜索下一个节点}
}
int main()
{int n,m,e;cin>>n>>m;memset(h,-1,sizeof h);char c[2];int x,y,z;while(m--){scanf("%d%d%d%s",&x,&y,&z,c);add(x,y,z);add(y,x,z);}dfs(1,0);ll ans=-1;for(int i=1;i<=n;i++)if(d[i]>ans){ans=d[i];e=i;}memset(d,0,sizeof d);dfs(e,0);for(int i=1;i<=n;i++)if(d[i]>ans)ans=d[i];printf("%lld",ans);return 0;
}

代码2（树形dp）

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
const int N=1e6+10;
int n,m;
long long ans;
long long e[N],h[N],ne[N],idx,w[N];
long long f1[N],f2[N];
void add(int x,int y,int z)
{e[idx]=y;w[idx]=z;ne[idx]=h[x];h[x]=idx++;
}
void dp(int x,int father)
{for(int i=h[x];i!=-1;i=ne[i]){int j=e[i];if(j==father) continue;//防止原路返回dp(j,x);if(f1[x]<f1[j]+w[i]){f2[x]=f1[x];f1[x]=f1[j]+w[i];}else if(f2[x]<f1[j]+w[i])f2[x]=f1[j]+w[i];ans=max(ans,f1[x]+f2[x]);}
}
int main()
{cin>>n>>m;char c;int x,y,z;memset(h,-1,sizeof h);for(int i=1;i<=m;i++){cin>>x>>y>>z>>c;add(x,y,z);add(y,x,z);}dp(1,0);printf("%lld",ans);return 0;
}

这就是基本的树的直径求解的两种方法。

如果有更好的方法，欢迎大家在评论区里留言！